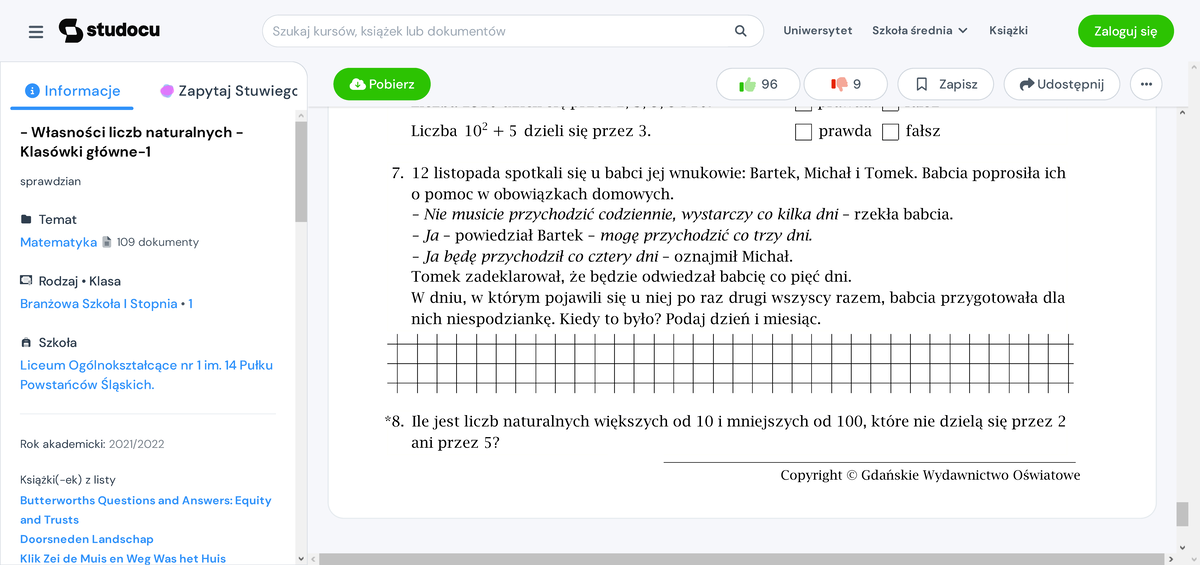
Sprawdzian Z Własności Liczb Naturalnych

Hej Studenci! Czy czeka Was Sprawdzian z Własności Liczb Naturalnych? Nie martwcie się! Ten artykuł rozłoży ten temat na czynniki pierwsze, tak żeby każdy, nawet bez super mocnej wiedzy matematycznej, mógł go zrozumieć. Postaramy się wyjaśnić wszystko krok po kroku, używając prostego języka i przykładów z życia wziętych. Gotowi?

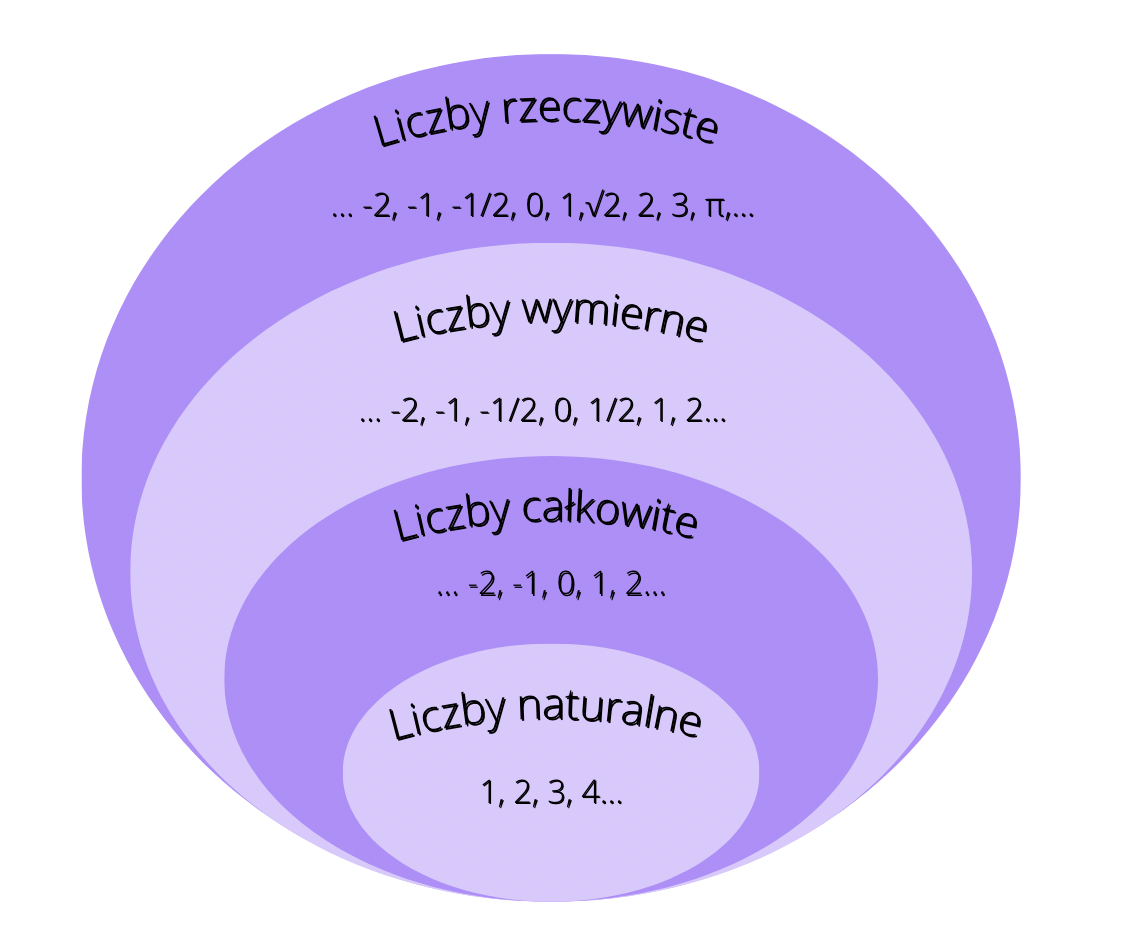
Czym w ogóle są liczby naturalne?

Zacznijmy od podstaw. Liczby naturalne to po prostu liczby, których używamy do liczenia. Myślimy o nich jak o jabłkach w koszyku, monetach w portfelu, albo krokach, które robimy idąc do szkoły. To liczby: 1, 2, 3, 4, 5, 6, 7, i tak dalej...aż do nieskończoności! Ważne jest, że nie zaliczamy do nich liczb ujemnych (np. -1, -2), ułamków (np. 1/2, 3/4) ani zera. Niektórzy matematycy włączają zero do zbioru liczb naturalnych, ale na potrzeby tego sprawdzianu, skupmy się na tych dodatnich.

Dzielniki i wielokrotności

Teraz przejdźmy do ważnych pojęć związanych z liczbami naturalnymi: dzielniki i wielokrotności.

Dzielnik liczby to taka liczba naturalna, która dzieli daną liczbę bez reszty. Na przykład, dzielnikami liczby 12 są: 1, 2, 3, 4, 6 i 12. Dlaczego? Bo 12 podzielone przez każdą z tych liczb daje nam inną liczbę naturalną, bez reszty.

Pomyśl o tym jak o dzieleniu pizzy. Jeśli masz 12 kawałków pizzy, możesz je równo rozdzielić między 1, 2, 3, 4, 6 lub 12 osób. Nie możesz jej równo podzielić między 5 osób, bo zostaną Ci resztki.

Wielokrotność liczby to liczba, którą otrzymujemy mnożąc daną liczbę przez jakąś inną liczbę naturalną. Na przykład, wielokrotnościami liczby 3 są: 3, 6, 9, 12, 15, 18, itd. Po prostu mnożymy 3 przez 1, 2, 3, 4, 5, 6, itd.

Wielokrotności to jak tabliczka mnożenia. Wielokrotności liczby 5 to po prostu to, co znajdziesz w tabliczce mnożenia dla 5: 5, 10, 15, 20, 25...

Liczby pierwsze i liczby złożone

Kolejne kluczowe pojęcia to liczby pierwsze i liczby złożone.

Liczba pierwsza to taka liczba naturalna większa od 1, która ma tylko dwa dzielniki: 1 i samą siebie. Na przykład, 2, 3, 5, 7, 11, 13, 17, 19 to liczby pierwsze. Liczba 7 dzieli się tylko przez 1 i przez 7.

Pomyśl o liczbach pierwszych jak o "atomach" w świecie liczb. Nie da się ich rozłożyć na mniejsze, całkowite kawałki (poza 1 i samą liczbą). Nie da się podzielić 7 jabłek między więcej niż 1 osobę lub 7 osób, tak żeby każdy dostał równą liczbę całych jabłek.

Liczba złożona to taka liczba naturalna większa od 1, która ma więcej niż dwa dzielniki. Na przykład, 4, 6, 8, 9, 10, 12 to liczby złożone. Liczba 6 dzieli się przez 1, 2, 3 i 6.

Liczby złożone to liczby, które można "zbudować" z mniejszych liczb, mnożąc je przez siebie. Na przykład 6 to 2 razy 3. Możemy podzielić 6 jabłek równo między 1, 2, 3 lub 6 osób.

Pamiętaj! Liczba 1 nie jest ani pierwsza, ani złożona. Jest specjalnym przypadkiem.

Rozkład na czynniki pierwsze

Rozkład na czynniki pierwsze to proces zapisywania liczby złożonej jako iloczyn liczb pierwszych. To jak rozebranie skomplikowanej budowli na pojedyncze cegły (liczby pierwsze).

Na przykład, rozkład liczby 12 na czynniki pierwsze to: 2 x 2 x 3. Możemy to zapisać też jako 2² x 3.

Jak to zrobić? Możemy użyć metody "drzewka". Zaczynamy od liczby, którą chcemy rozłożyć, i dzielimy ją na dwa czynniki. Potem każdy z tych czynników, jeśli jest liczbą złożoną, dzielimy dalej, aż dojdziemy do liczb pierwszych.

Przykład: rozkładamy liczbę 36.

1. 36 dzielimy na 4 i 9
2. 4 dzielimy na 2 i 2 (obie to liczby pierwsze)
3. 9 dzielimy na 3 i 3 (obie to liczby pierwsze)

Więc rozkład liczby 36 na czynniki pierwsze to: 2 x 2 x 3 x 3, czyli 2² x 3².

Cechy podzielności

Cechy podzielności to proste zasady, które pozwalają nam szybko sprawdzić, czy dana liczba dzieli się przez inną liczbę bez reszty. Znajomość tych cech bardzo ułatwia zadania na sprawdzianie!

• Podzielność przez 2: Liczba dzieli się przez 2, jeśli jej ostatnia cyfra jest parzysta (0, 2, 4, 6, 8). Na przykład, 124, 356, 780 dzielą się przez 2.
• Podzielność przez 3: Liczba dzieli się przez 3, jeśli suma jej cyfr dzieli się przez 3. Na przykład, 123 (1+2+3=6, a 6 dzieli się przez 3), 456 (4+5+6=15, a 15 dzieli się przez 3), 789 (7+8+9=24, a 24 dzieli się przez 3).
• Podzielność przez 4: Liczba dzieli się przez 4, jeśli liczba utworzona przez jej dwie ostatnie cyfry dzieli się przez 4. Na przykład, 112 (12 dzieli się przez 4), 236 (36 dzieli się przez 4), 580 (80 dzieli się przez 4).
• Podzielność przez 5: Liczba dzieli się przez 5, jeśli jej ostatnia cyfra to 0 lub 5. Na przykład, 125, 340, 675 dzielą się przez 5.
• Podzielność przez 9: Liczba dzieli się przez 9, jeśli suma jej cyfr dzieli się przez 9. Na przykład, 189 (1+8+9=18, a 18 dzieli się przez 9), 270 (2+7+0=9, a 9 dzieli się przez 9), 549 (5+4+9=18, a 18 dzieli się przez 9).
• Podzielność przez 10: Liczba dzieli się przez 10, jeśli jej ostatnia cyfra to 0. Na przykład, 120, 340, 670 dzielą się przez 10.

Największy wspólny dzielnik (NWD) i najmniejsza wspólna wielokrotność (NWW)

Na koniec, porozmawiajmy o największym wspólnym dzielniku (NWD) i najmniejszej wspólnej wielokrotności (NWW) dwóch lub więcej liczb.

NWD to największa liczba, która dzieli obie (lub wszystkie) liczby bez reszty. Na przykład, NWD(12, 18) = 6, ponieważ 6 jest największą liczbą, która dzieli zarówno 12, jak i 18.

Wyobraź sobie, że masz 12 cukierków i 18 ciastek. Chcesz zrobić paczki, w których każda paczka ma taką samą liczbę cukierków i taką samą liczbę ciastek. Jaka jest największa liczba paczek, które możesz zrobić? To właśnie NWD!

NWW to najmniejsza liczba, która jest wielokrotnością obu (lub wszystkich) liczb. Na przykład, NWW(4, 6) = 12, ponieważ 12 jest najmniejszą liczbą, która dzieli się zarówno przez 4, jak i przez 6.

Wyobraź sobie, że masz dwa autobusy. Jeden odjeżdża co 4 minuty, a drugi co 6 minut. Co ile minut oba autobusy odjadą jednocześnie? To właśnie NWW!

Jak znaleźć NWD i NWW? Możemy użyć metody rozkładu na czynniki pierwsze. Rozkładamy każdą liczbę na czynniki pierwsze.

Przykład: znajdź NWD(24, 36) i NWW(24, 36).

• 24 = 2 x 2 x 2 x 3 = 2³ x 3
• 36 = 2 x 2 x 3 x 3 = 2² x 3²

NWD: Wybieramy czynniki pierwsze, które występują w obu rozkładach, w najniższej potędze. Czyli 2² x 3 = 4 x 3 = 12. NWD(24, 36) = 12.

NWW: Wybieramy wszystkie czynniki pierwsze, które występują w rozkładach, w najwyższej potędze. Czyli 2³ x 3² = 8 x 9 = 72. NWW(24, 36) = 72.

I to tyle! Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć właściwości liczb naturalnych. Pamiętaj, ćwicz regularnie, rozwiązuj zadania i nie bój się pytać! Powodzenia na sprawdzianie!