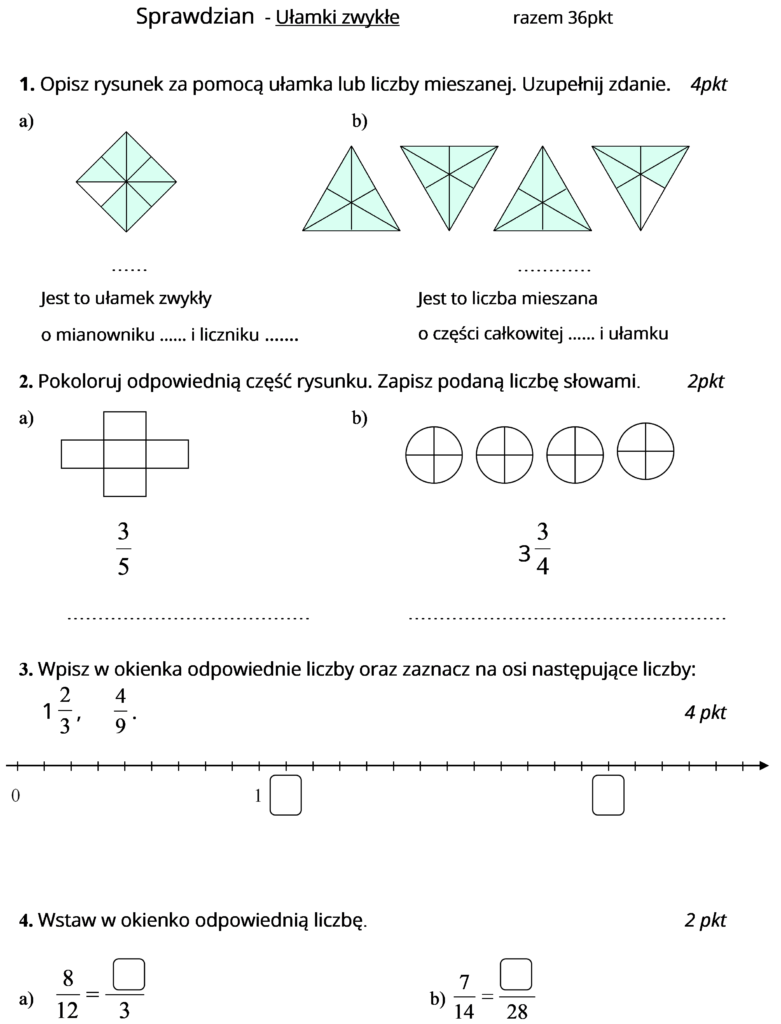
Sprawdzian Z Ułamków Zwykłych Klasa 4 Matematyka Wokół Nas

Ułamki zwykłe. Dziś temat, który potrafi spędzić sen z powiek niejednego czwartoklasisty (i nie tylko!). Ale spokojnie, nie taki diabeł straszny, jak go malują. Przygotujmy się razem do sprawdzianu z ułamków zwykłych, bazując na podręczniku "Matematyka Wokół Nas" dla klasy 4. Zamiast stresu, spróbujmy znaleźć w tym trochę zabawy i satysfakcji z pokonywania kolejnych matematycznych wyzwań.

Zacznijmy od podstaw. Co to właściwie jest ten ułamek zwykły? To nic innego jak sposób na zapisanie części całości. Mamy dwie liczby: licznik (na górze) i mianownik (na dole), oddzielone kreską ułamkową. Mianownik mówi nam, na ile równych części podzieliliśmy całość, a licznik – ile z tych części bierzemy.

Wyobraź sobie pizzę. Jeśli pokroimy ją na 8 równych kawałków (mianownik = 8), a Ty zjesz 3 z nich (licznik = 3), to zjadłeś 3/8 pizzy. Proste, prawda?

Teraz przejdźmy do typowych zadań, które mogą pojawić się na sprawdzianie.

Porównywanie Ułamków

Porównywanie ułamków to umiejętność określenia, który ułamek jest większy, mniejszy lub czy są równe. To kluczowa umiejętność, bo pozwala nam uporządkować liczby i zrozumieć ich wzajemne relacje.

Zacznijmy od najprostszego przypadku: ułamki o tym samym mianowniku. Wtedy sprawa jest banalna – wystarczy porównać liczniki. Im większy licznik, tym większy ułamek. Na przykład, 5/7 jest większe od 2/7, bo 5 jest większe od 2. Wizualizacja też tu pomaga. Wyobraź sobie tort pokrojony na 7 kawałków. Pięć kawałków to więcej niż dwa.

Co, jeśli ułamki mają różne mianowniki? Tutaj musimy wykonać pewien trik: sprowadzić je do wspólnego mianownika. To znaczy znaleźć taką liczbę, która jest wielokrotnością obu mianowników. Najlepiej od razu szukać najmniejszej wspólnej wielokrotności (NWW), żeby obliczenia były prostsze.

Powiedzmy, że mamy ułamki 1/3 i 1/4. NWW dla 3 i 4 to 12. Musimy więc "rozszerzyć" oba ułamki tak, żeby miały mianownik 12. Ułamek 1/3 rozszerzamy przez 4 (mnożymy licznik i mianownik przez 4), otrzymując 4/12. Ułamek 1/4 rozszerzamy przez 3, otrzymując 3/12. Teraz możemy łatwo porównać: 4/12 jest większe od 3/12, więc 1/3 jest większe od 1/4.

Inny przykład: porównaj 2/5 i 3/10. NWW dla 5 i 10 to 10. Ułamek 2/5 rozszerzamy przez 2, otrzymując 4/10. Ułamek 3/10 już ma mianownik 10, więc nie musimy go zmieniać. Porównujemy: 4/10 jest większe od 3/10, więc 2/5 jest większe od 3/10.

Pamiętaj: rozszerzając ułamek, mnożymy zarówno licznik, jak i mianownik przez tę samą liczbę. Dzięki temu wartość ułamka się nie zmienia, tylko zmienia się jego zapis. To jakbyś pokroił pizzę na więcej kawałków, ale w sumie masz tyle samo pizzy.

Czasem zdarza się, że mamy ułamki o różnych licznikach i mianownikach, ale jeden z ułamków jest bliski 0, a drugi bliski 1. Wtedy możemy od razu stwierdzić, który jest większy. Na przykład, 1/100 jest dużo mniejsze niż 99/100.

Warto też pamiętać o ułamkach równych 1. Każdy ułamek, w którym licznik jest równy mianownikowi, jest równy 1. Na przykład, 5/5 = 1, 12/12 = 1. Porównując ułamek do 1, możemy szybko ocenić, czy jest on większy czy mniejszy od 1. Jeśli licznik jest mniejszy od mianownika, to ułamek jest mniejszy od 1. Jeśli licznik jest większy od mianownika, to ułamek jest większy od 1 (wtedy mamy do czynienia z ułamkiem niewłaściwym, o czym za chwilę).

Ćwiczenia, ćwiczenia i jeszcze raz ćwiczenia! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zasadę porównywania ułamków i tym szybciej będziesz w stanie to robić. Poszukaj zadań w podręczniku "Matematyka Wokół Nas", w zbiorach zadań, a nawet w internecie.

Dodawanie i Odejmowanie Ułamków

Dodawanie i odejmowanie ułamków przypomina trochę porównywanie. Tu również kluczowe jest posiadanie wspólnego mianownika. Jeśli go mamy, sprawa jest prosta: dodajemy lub odejmujemy liczniki, a mianownik pozostaje bez zmian.

Przykład: 2/7 + 3/7 = 5/7. Mamy wspólny mianownik (7), więc dodajemy liczniki (2 + 3 = 5). Wynik to 5/7.

Odejmowanie działa analogicznie: 5/8 - 2/8 = 3/8. Mamy wspólny mianownik (8), więc odejmujemy liczniki (5 - 2 = 3). Wynik to 3/8.

Co, jeśli ułamki nie mają wspólnego mianownika? Znowu musimy je sprowadzić do wspólnego mianownika, tak jak przy porównywaniu. Szukamy NWW mianowników i rozszerzamy ułamki.

Przykład: 1/4 + 1/6. NWW dla 4 i 6 to 12. Ułamek 1/4 rozszerzamy przez 3, otrzymując 3/12. Ułamek 1/6 rozszerzamy przez 2, otrzymując 2/12. Teraz możemy dodać: 3/12 + 2/12 = 5/12.

Inny przykład: 2/3 - 1/2. NWW dla 3 i 2 to 6. Ułamek 2/3 rozszerzamy przez 2, otrzymując 4/6. Ułamek 1/2 rozszerzamy przez 3, otrzymując 3/6. Teraz możemy odjąć: 4/6 - 3/6 = 1/6.

Pamiętaj, żeby zawsze sprawdzić, czy wynik można skrócić. Skracanie ułamka to dzielenie licznika i mianownika przez tę samą liczbę, aż nie będzie można ich już podzielić (czyli aż będą względnie pierwsze). Na przykład, 4/8 można skrócić przez 4, otrzymując 1/2.

Czasami w zadaniach pojawiają się liczby mieszane, czyli liczby składające się z części całkowitej i ułamkowej, np. 1 1/2 (jeden i jedna druga). Żeby dodać lub odjąć liczby mieszane, możemy zamienić je na ułamki niewłaściwe (czyli ułamki, w których licznik jest większy od mianownika) i wtedy wykonywać działania.

Jak zamienić liczbę mieszaną na ułamek niewłaściwy? Mnożymy część całkowitą przez mianownik ułamka i dodajemy licznik. To, co otrzymamy, to licznik ułamka niewłaściwego. Mianownik pozostaje ten sam. Na przykład, 1 1/2 = (1 * 2 + 1) / 2 = 3/2.

Inny przykład: 2 3/4 = (2 * 4 + 3) / 4 = 11/4.

Po wykonaniu dodawania lub odejmowania ułamków niewłaściwych, możemy zamienić wynik z powrotem na liczbę mieszaną. Dzielimy licznik przez mianownik. Wynik dzielenia to część całkowita liczby mieszanej. Reszta z dzielenia to licznik ułamka, a mianownik pozostaje ten sam. Na przykład, 7/3 = 2 1/3 (bo 7 podzielone przez 3 to 2 reszty 1).

Pamiętaj, że ćwiczenie czyni mistrza! Rozwiązuj zadania z dodawania i odejmowania ułamków, zarówno te z podręcznika, jak i te dodatkowe. Im więcej będziesz ćwiczyć, tym łatwiej przyjdą Ci te obliczenia.

Ułamki Niewłaściwe i Liczby Mieszane

Ułamek niewłaściwy to taki ułamek, którego licznik jest większy lub równy mianownikowi, np. 5/3, 7/7, 10/4. Oznacza to, że mamy więcej niż jedną całość. Liczba mieszana to połączenie liczby całkowitej i ułamka właściwego, np. 1 2/3, 3 1/4. Oba te zapisy reprezentują tę samą wartość, tylko w inny sposób.

Jak zamienić ułamek niewłaściwy na liczbę mieszaną? Dzielimy licznik przez mianownik. Wynik dzielenia to część całkowita liczby mieszanej. Reszta z dzielenia to licznik ułamka, a mianownik pozostaje bez zmian. Przykład: 7/3. 7 podzielone przez 3 to 2 reszty 1. Zatem 7/3 = 2 1/3.

Inny przykład: 11/4. 11 podzielone przez 4 to 2 reszty 3. Zatem 11/4 = 2 3/4.

Inny przykład: 2 3/4. 2 pomnożone przez 4 to 8, plus 3 to 11. Zatem 2 3/4 = 11/4.

Umiejętność zamiany między ułamkami niewłaściwymi a liczbami mieszanymi jest bardzo przydatna przy wykonywaniu działań na ułamkach. Często łatwiej jest dodawać lub odejmować ułamki, jeśli zamienimy je na ułamki niewłaściwe. Po wykonaniu działania możemy z powrotem zamienić wynik na liczbę mieszaną, jeśli jest to bardziej czytelne.

Zadania Tekstowe z Ułamkami

Zadania tekstowe to często element sprawdzianu, który sprawia najwięcej trudności. Kluczem do sukcesu jest uważne czytanie ze zrozumieniem i identyfikacja, o jakie działanie chodzi.

Przykład: Kasia zjadła 1/3 ciasta, a Basia 1/4 ciasta. Ile ciasta zjadły razem?

Tutaj musimy dodać ułamki 1/3 i 1/4. Sprowadzamy je do wspólnego mianownika (12): 1/3 = 4/12, 1/4 = 3/12. Dodajemy: 4/12 + 3/12 = 7/12. Odpowiedź: Kasia i Basia zjadły razem 7/12 ciasta.

Inny przykład: Mama kupiła 2 1/2 kg jabłek. Na szarlotkę zużyła 1 1/4 kg jabłek. Ile jabłek zostało?

Tutaj musimy odjąć ułamki: 2 1/2 - 1 1/4. Zamieniamy liczby mieszane na ułamki niewłaściwe: 2 1/2 = 5/2, 1 1/4 = 5/4. Sprowadzamy ułamki do wspólnego mianownika (4): 5/2 = 10/4. Odejmujemy: 10/4 - 5/4 = 5/4. Zamieniamy ułamek niewłaściwy na liczbę mieszaną: 5/4 = 1 1/4. Odpowiedź: Zostało 1 1/4 kg jabłek.

Pamiętaj, żeby zawsze pisać odpowiedź do zadania tekstowego! Odpowiedź powinna być sformułowana pełnym zdaniem i odpowiadać na pytanie zawarte w zadaniu.

Przed Tobą sprawdzian z ułamków? Powodzenia! Pamiętaj, że kluczem jest zrozumienie zasad i dużo ćwiczeń. Nie stresuj się, podejdź do tego jak do wyzwania, które możesz pokonać. A po sprawdzianie – zasłużony odpoczynek i może… pizza podzielona na ułamki!