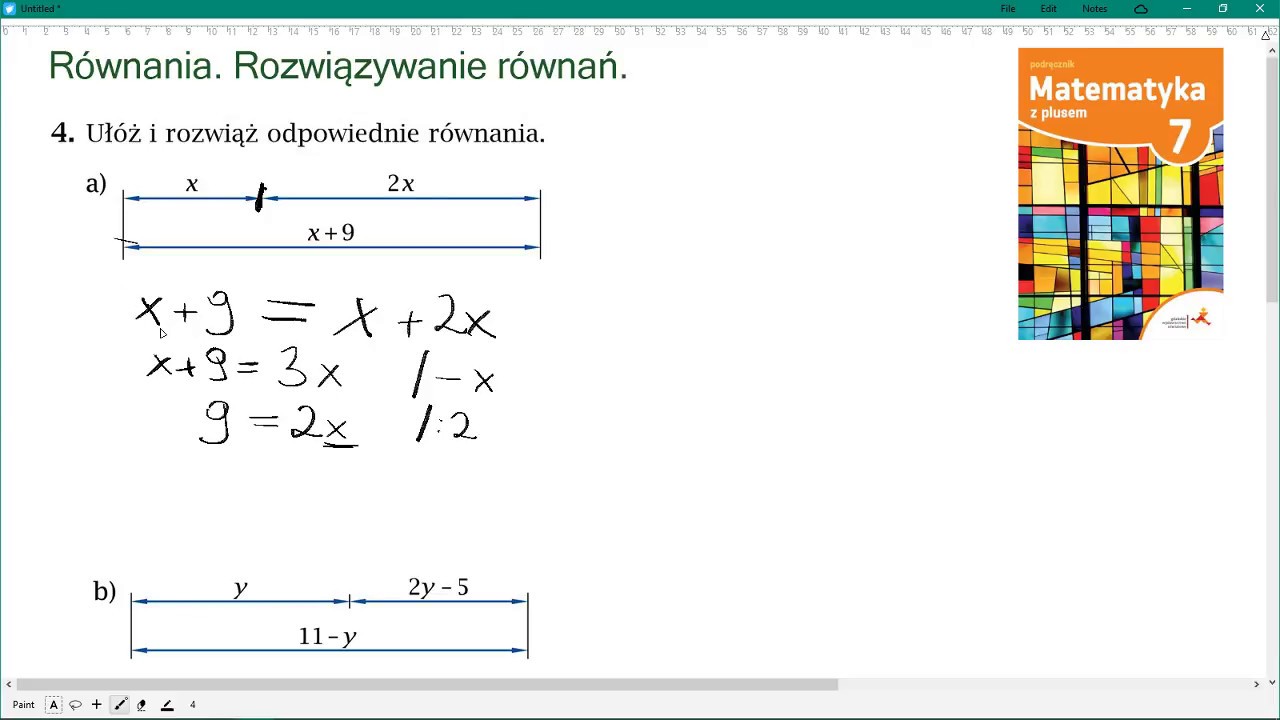
Sprawdzian Z Równań Klasa 7

Czy zbliża się sprawdzian z równań w 7 klasie? Czujesz stres i nie wiesz, od czego zacząć przygotowania? Spokojnie, nie jesteś sam! Równania to fundament algebry, a opanowanie ich to klucz do sukcesu w dalszej nauce matematyki. Ten artykuł jest dla Ciebie – ucznia 7 klasy, który chce zrozumieć równania, dobrze napisać sprawdzian i poczuć się pewnie z tym zagadnieniem. Przygotuj się na podróż po świecie równań, gdzie znajdziesz praktyczne porady, przykłady i sprawdzone metody nauki.

Czym są Równania i Dlaczego są Tak Ważne?

Równanie to nic innego jak stwierdzenie, że dwa wyrażenia matematyczne są sobie równe. Wygląda to mniej więcej tak: a = b. Ale w matematyce szkolnej, a szczególnie w 7 klasie, zwykle mamy do czynienia z równaniami zawierającymi niewiadome, które oznaczamy literami (najczęściej x, y, z). Naszym celem jest znalezienie wartości tej niewiadomej, która sprawia, że równanie jest prawdziwe.

Dlaczego równania są tak ważne? Oto kilka powodów:

• Rozwiązywanie problemów: Równania pozwalają nam opisywać i rozwiązywać problemy z życia codziennego, np. obliczanie, ile cukierków kupisz za daną kwotę, jeśli znasz cenę jednego cukierka.
• Budowanie podstaw algebry: Zrozumienie równań jest kluczowe do dalszej nauki algebry, a algebra jest potrzebna w wielu dziedzinach nauki i techniki.
• Rozwój logicznego myślenia: Rozwiązywanie równań uczy logicznego myślenia, analizowania i wyciągania wniosków.

Wyobraź sobie, że masz wagę szalkową. Na jednej szalce kładziesz 3 cukierki i na drugiej nieznaną liczbę cukierków. Waga jest w równowadze, gdy na obu szalkach jest tyle samo cukierków. To jest właśnie równanie! Musisz znaleźć, ile cukierków jest na drugiej szalce (czyli znaleźć wartość niewiadomej), żeby waga była w równowadze.

Rodzaje Równań, Które Spotkasz w 7 Klasie

W 7 klasie najczęściej spotkasz się z następującymi rodzajami równań:

• Równania liniowe z jedną niewiadomą: To najprostszy typ równań, np. 2x + 3 = 7.
• Równania z nawiasami: Trzeba najpierw uprościć wyrażenie, pozbywając się nawiasów, np. 3(x – 2) = 9.
• Równania z ułamkami: Wymagają sprowadzenia ułamków do wspólnego mianownika, np. x/2 + 1/3 = 5/6.
• Równania, które trzeba uprościć: Przed rozwiązaniem trzeba uprościć obie strony równania, np. 3x + 2 – x = 5x – 4.

Jak Rozwiązywać Równania Krok po Kroku?

Rozwiązywanie równań to proces, który można podzielić na kilka kroków. Pamiętaj, że kluczem jest równowaga – to, co robisz z jednej strony równania, musisz zrobić również z drugiej.

1. Uprość obie strony równania: Pozbądź się nawiasów (pamiętaj o mnożeniu każdego elementu w nawiasie), redukuj wyrazy podobne (dodaj lub odejmij wyrazy z tą samą niewiadomą i liczby).
2. Przenieś niewiadome na jedną stronę równania, a liczby na drugą: Pamiętaj, że przenosząc wyraz na drugą stronę równania, zmieniasz jego znak na przeciwny. Na przykład, jeśli masz x + 2 = 5, przenosisz +2 na prawą stronę i otrzymujesz x = 5 – 2.
3. Wykonaj działania: Zsumuj lub odejmij liczby po obu stronach równania.
4. Podziel obie strony równania przez współczynnik przy niewiadomej: Jeśli masz 2x = 6, dzielisz obie strony przez 2 i otrzymujesz x = 3.
5. Sprawdź rozwiązanie: Podstaw znalezioną wartość niewiadomej do oryginalnego równania i sprawdź, czy lewa strona równania jest równa prawej stronie. Jeśli tak, to rozwiązanie jest poprawne.

Przykład: Rozwiąż równanie 4x – 5 = 2x + 1.

1. Uprość obie strony: Obie strony są już uproszczone.
2. Przenieś niewiadome na lewą stronę, a liczby na prawą: 4x – 2x = 1 + 5
3. Wykonaj działania: 2x = 6
4. Podziel obie strony przez współczynnik przy niewiadomej: x = 6 / 2
5. Rozwiązanie: x = 3
6. Sprawdzenie: 4 * 3 – 5 = 2 * 3 + 1; 12 – 5 = 6 + 1; 7 = 7. Rozwiązanie jest poprawne.

Pułapki i Jak Ich Unikać

Podczas rozwiązywania równań łatwo popełnić błąd. Oto kilka typowych pułapek i jak ich unikać:

• Zapominanie o zmianie znaku przy przenoszeniu wyrazów: Pamiętaj, że przenosząc wyraz na drugą stronę równania, musisz zmienić jego znak na przeciwny. To bardzo ważne!
• Błędy w kolejności wykonywania działań: Pamiętaj o kolejności: nawiasy, potęgowanie, mnożenie i dzielenie (od lewej do prawej), dodawanie i odejmowanie (od lewej do prawej).
• Błędy przy redukcji wyrazów podobnych: Upewnij się, że dodajesz lub odejmujesz tylko wyrazy z tą samą niewiadomą.
• Złe mnożenie przez nawias: Pamiętaj, żeby pomnożyć każdy element w nawiasie przez liczbę przed nawiasem. Na przykład, 3(x + 2) = 3x + 6.
• Błędy przy sprowadzaniu ułamków do wspólnego mianownika: Upewnij się, że poprawnie rozszerzasz liczniki i mianowniki ułamków.

Rada: Zawsze sprawdzaj swoje rozwiązanie, podstawiając je do oryginalnego równania. To najlepszy sposób na uniknięcie błędów!

Jak Skutecznie Przygotować się do Sprawdzianu?

Przygotowanie do sprawdzianu z równań wymaga systematyczności i odpowiedniego podejścia. Oto kilka wskazówek:

• Przejrzyj notatki z lekcji: Upewnij się, że rozumiesz wszystkie definicje i zasady.
• Rozwiąż zadania z podręcznika i zeszytu ćwiczeń: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz temat.
• Skorzystaj z dostępnych zasobów online: W Internecie znajdziesz wiele materiałów edukacyjnych, takich jak filmy instruktażowe, interaktywne ćwiczenia i testy.
• Poproś o pomoc nauczyciela lub kolegę: Jeśli masz problemy z jakimś zagadnieniem, nie bój się prosić o pomoc.
• Powtórz zadania z poprzednich sprawdzianów: To dobry sposób na sprawdzenie swojej wiedzy i zidentyfikowanie obszarów, które wymagają dodatkowej pracy.
• Rozwiąż przykładowe arkusze sprawdzianowe: Symulacja sprawdzianu pomoże Ci oswoić się ze stresem i sprawdzić, ile czasu potrzebujesz na rozwiązanie różnych typów zadań.
• Odpocznij przed sprawdzianem: Wyspany i wypoczęty umysł lepiej radzi sobie ze stresem i koncentracją.

Przykładowe Zadania Sprawdzianowe (z Rozwiązaniami)

Oto kilka przykładowych zadań, które mogą pojawić się na sprawdzianie z równań w 7 klasie:

1. Rozwiąż równanie: 3x + 5 = 14.
   • Rozwiązanie: 3x = 14 – 5; 3x = 9; x = 9 / 3; x = 3.
2. Rozwiąż równanie: 2(x – 1) = 6.
   • Rozwiązanie: 2x – 2 = 6; 2x = 6 + 2; 2x = 8; x = 8 / 2; x = 4.
3. Rozwiąż równanie: x/4 + 1/2 = 3/4.
   • Rozwiązanie: x/4 = 3/4 – 1/2; x/4 = 3/4 – 2/4; x/4 = 1/4; x = 1.
4. Rozwiąż równanie: 5x – 3 + x = 2x + 9.
   • Rozwiązanie: 6x – 3 = 2x + 9; 6x – 2x = 9 + 3; 4x = 12; x = 12 / 4; x = 3.
5. Zadanie tekstowe: Mama kupiła 3 kg jabłek i 2 kg gruszek. Zapłaciła łącznie 17 zł. Kilogram jabłek kosztował 4 zł. Ile kosztował kilogram gruszek?
   • Rozwiązanie: Niech x oznacza cenę kilograma gruszek. Równanie: 3 * 4 + 2 * x = 17; 12 + 2x = 17; 2x = 17 – 12; 2x = 5; x = 5 / 2; x = 2.5. Odpowiedź: Kilogram gruszek kosztował 2.5 zł.

Równania w Życiu Codziennym: Przykłady

Może się wydawać, że równania to tylko abstrakcyjne symbole i liczby, ale tak naprawdę otaczają nas one na każdym kroku. Oto kilka przykładów:

• Gotowanie: Przepis na ciasto wymaga określonej ilości składników. Jeśli chcesz upiec większe ciasto, musisz proporcjonalnie zwiększyć ilość każdego składnika, wykorzystując do tego równania.
• Zakupy: Obliczanie, ile zapłacisz za kilka produktów, korzystając z cen jednostkowych, to nic innego jak rozwiązywanie równania.
• Planowanie podróży: Obliczanie czasu podróży, biorąc pod uwagę odległość i prędkość, również wymaga użycia równań. Np. czas = odległość / prędkość.
• Finanse: Obliczanie oprocentowania kredytu, wysokości raty, czy oszczędności, to wszystko zadania, które wymagają umiejętności rozwiązywania równań.
• Sport: Obliczanie średniej prędkości biegacza, kąta rzutu oszczepem, czy trajektorii lotu piłki, korzysta z równań fizycznych.

Dzięki umiejętności rozwiązywania równań, możesz lepiej zrozumieć świat wokół siebie i podejmować bardziej świadome decyzje.

Zakończenie: Równania to Klucz do Sukcesu!

Sprawdzian z równań w 7 klasie to ważny krok w Twojej edukacyjnej podróży. Mam nadzieję, że ten artykuł pomógł Ci lepiej zrozumieć równania, poczuć się pewniej i przygotować się do sprawdzianu. Pamiętaj, że ćwiczenie czyni mistrza. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz temat i tym większa będzie Twoja pewność siebie.

Nie bój się pytać o pomoc, korzystaj z dostępnych zasobów i pamiętaj, że równania to nie tylko abstrakcyjne symbole, ale narzędzie, które pozwala nam zrozumieć i opisywać świat wokół nas. Życzę Ci powodzenia na sprawdzianie i w dalszej nauce matematyki! Pamiętaj, Ty dasz radę!