Sprawdzian Z Prostych I Mierzenia Kątów Klasa 4

Sprawdzian z prostych i mierzenia kątów w klasie 4 sprawdza, czy rozumiesz podstawowe pojęcia z geometrii, takie jak czym są proste, półproste, odcinki i jak mierzyć kąty. Znajomość tych zagadnień jest bardzo ważna, ponieważ geometria otacza nas wszędzie – w architekturze budynków, w układzie ulic, a nawet w budowie przedmiotów codziennego użytku. Pomyśl o stolarzu, który musi precyzyjnie mierzyć kąty, żeby zbudować krzesło. Podobnie, architekt planuje budynki, używając zasad geometrii. Nawet w grach komputerowych, twórcy wykorzystują geometrię do tworzenia przestrzeni i obiektów!

Ten artykuł ma na celu pomóc Ci przygotować się do sprawdzianu. Przejdziemy krok po kroku przez najważniejsze zagadnienia, z przykładami i wskazówkami, które pomogą Ci zrozumieć i zapamiętać materiał.

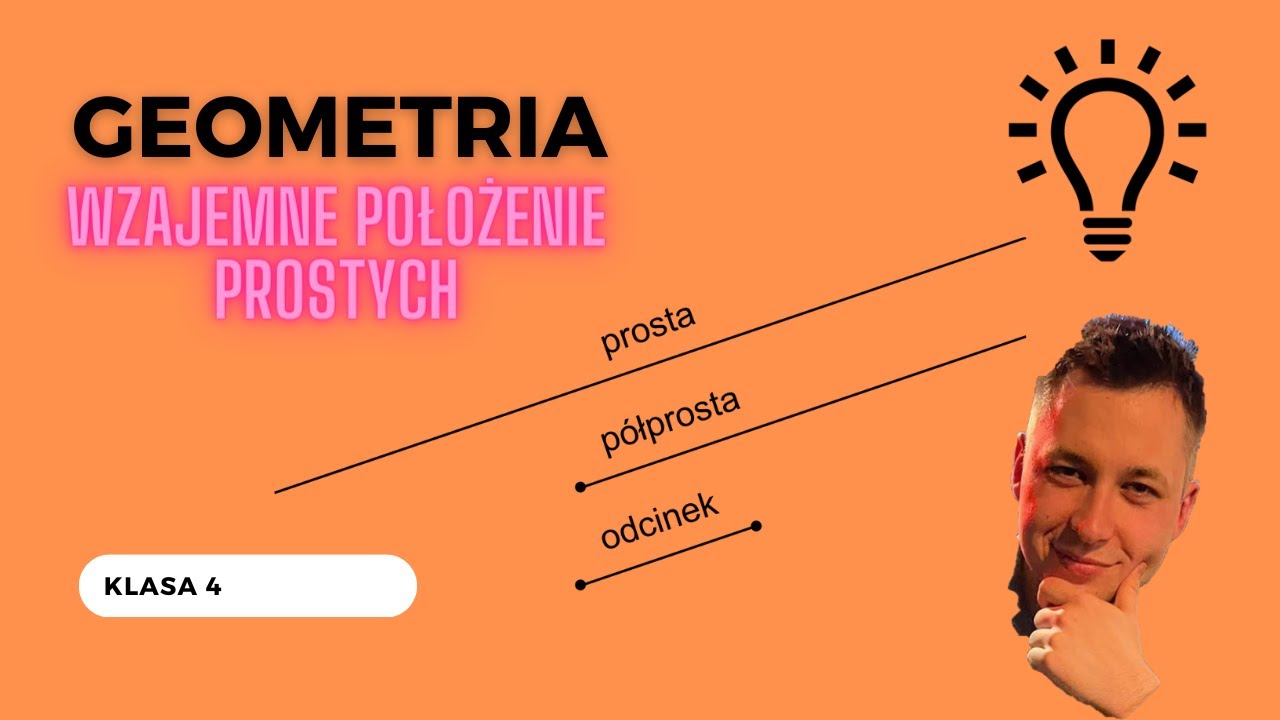
Podstawowe Pojęcia: Proste, Półproste i Odcinki

Zacznijmy od podstawowych elementów geometrii:

Prosta: Prosta jest nieskończona w obu kierunkach. Nie ma początku ani końca. Wyobraź sobie linię, która ciągnie się w nieskończoność. Na rysunku prostą oznaczamy literami małymi (np. prosta *k*) lub dwoma punktami leżącymi na tej prostej (np. prosta AB).
Półprosta: Półprosta ma początek, ale nie ma końca. Wyobraź sobie promień światła – zaczyna się w źródle światła (np. w żarówce), ale rozchodzi się w nieskończoność. Półprosta oznaczamy podając jej początek i dowolny inny punkt na niej (np. półprosta AB, gdzie A jest początkiem). WAŻNE: Zawsze zaczynamy od punktu początkowego!
Odcinek: Odcinek ma początek i koniec. Jest to fragment prostej ograniczony dwoma punktami. Wyobraź sobie kawałek sznurka – ma początek i koniec. Odcinek oznaczamy dwoma punktami, które go ograniczają (np. odcinek AB).

Przykład: Wyobraź sobie drogę. Jeśli droga ciągnie się w nieskończoność w obie strony, to jest to prosta. Jeśli droga zaczyna się w Twoim domu i biegnie w jednym kierunku, to jest to półprosta. A odcinek drogi między Twoim domem a sklepem to odcinek.

Mierzenie Kątów

Kąt to figura geometryczna utworzona przez dwie półproste wychodzące z jednego punktu, zwanego wierzchołkiem kąta. Miarę kąta wyrażamy w stopniach (symbol: °). Do mierzenia kątów używamy kątomierza.

Rodzaje Kątów:

Kąt ostry: Mniejszy niż 90°.
Kąt prosty: Równy 90°. Wygląda jak róg kartki.
Kąt rozwarty: Większy niż 90° i mniejszy niż 180°.
Kąt półpełny: Równy 180°. Tworzy linię prostą.
Kąt pełny: Równy 360°.

Jak Mierzyć Kąty Kątomierzem?

Krok 1: Przyłóż środek kątomierza (zazwyczaj oznaczony małą dziurką lub krzyżykiem) do wierzchołka kąta.
Krok 2: Ustaw kątomierz tak, aby jedna z półprostych pokrywała się z 0° na skali kątomierza. Upewnij się, że patrzysz na odpowiednią skalę (czasem są dwie skale na kątomierzu!).
Krok 3: Sprawdź, gdzie druga półprosta przecina skalę kątomierza. Odczytaj wartość kąta.

Przykład: Wyobraź sobie, że mierzysz kąt między wskazówkami zegara o godzinie 1:00. Wierzchołek kąta to środek zegara. Jedna wskazówka (godzinowa) pokrywa się z cyfrą 1, a druga (minutowa) z cyfrą 12. Przykładając kątomierz, zobaczysz, że kąt ma około 30° (kąt ostry).

Ćwiczenia i Przykłady

Spróbuj rozwiązać poniższe zadania, aby sprawdzić swoją wiedzę:

Zadanie 1: Narysuj odcinek AB o długości 5 cm.
Zadanie 2: Narysuj półprostą o początku w punkcie C.
Zadanie 3: Zmierz kąt narysowany poniżej (przykładowy rysunek kąta do narysowania, np. kąt 60°).
Zadanie 4: Jaki kąt tworzą wskazówki zegara o godzinie 3:00? (Odpowiedź: kąt prosty, 90°)
Zadanie 5: Narysuj kąt rozwarty i zmierz go kątomierzem.

Wskazówki:

Pamiętaj o dokładnym przyłożeniu kątomierza. Małe przesunięcie może spowodować błąd w pomiarze.
Zwróć uwagę na jednostki. Miarę kąta wyrażamy w stopniach (°).
Ćwicz regularnie! Im więcej ćwiczysz, tym łatwiej będzie Ci mierzyć kąty i rozpoznawać różne rodzaje figur geometrycznych.

Jeśli masz problemy z jakimkolwiek zadaniem, poproś o pomoc nauczyciela, rodzica lub kolegę. Możesz również poszukać dodatkowych materiałów w Internecie lub w podręczniku do matematyki. Powodzenia na sprawdzianie!