Sprawdzian Z Pola Figur Klasa 4

Czy Twój czwartoklasista ma wkrótce sprawdzian z pola figur i czujesz, że potrzebuje małego wsparcia? A może jesteś nauczycielem szukającym sposobów na przygotowanie uczniów do tego ważnego testu? Ten artykuł jest właśnie dla Ciebie! Skupimy się na tym, jak efektywnie przygotować się do sprawdzianu z pola figur w klasie 4, tak aby matematyka stała się zrozumiała i przyjemna, a nie tylko stresującym obowiązkiem.

Co musisz wiedzieć przed sprawdzianem z pola figur w klasie 4?

Sprawdzian z pola figur w klasie 4 to często pierwszy poważny sprawdzian z geometrii dla młodych uczniów. Ważne jest, aby zrozumieć, jakie konkretnie zagadnienia będą na nim poruszane. Najczęściej obejmuje on:

Rozumienie pojęcia pola powierzchni. Czyli czym właściwie jest to pole i jak je mierzymy.
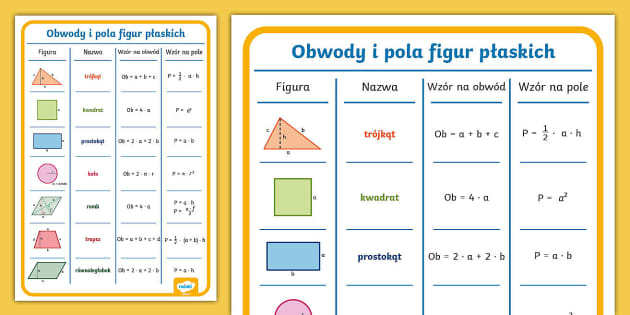
Obliczanie pola kwadratu i prostokąta. Podstawowe wzory i ich praktyczne zastosowanie.
Pojęcie jednostek pola powierzchni. Milimetry kwadratowe, centymetry kwadratowe, metry kwadratowe.
Porównywanie pól figur. Ustalanie, która figura ma większe lub mniejsze pole.
Rozwiązywanie zadań tekstowych. Wykorzystanie wiedzy o polu figur do rozwiązywania problemów z życia codziennego.

Zatem, zanim przystąpimy do nauki, upewnijmy się, że nasz uczeń (lub my sami, jeśli jesteśmy nauczycielem) ma jasność co do zakresu materiału. Warto przejrzeć podręcznik, zeszyt i sprawdzić, jakie zadania były rozwiązywane na lekcjach. To da nam solidną podstawę do dalszej pracy.

Jak efektywnie przygotować się do sprawdzianu?

Przygotowanie do sprawdzianu z pola figur nie musi być nudne i stresujące. Możemy wykorzystać różne metody, aby uczynić je bardziej angażującym i skutecznym. Oto kilka propozycji:

1. Zacznij od podstaw: zrozumienie, a nie wkuwanie.

Kluczem do sukcesu jest zrozumienie, czym właściwie jest pole powierzchni. Wyobraź sobie, że chcesz pomalować ścianę. Pole powierzchni tej ściany to ilość farby, której będziesz potrzebować. Im większa ściana, tym więcej farby. To właśnie jest pole! Starajmy się unikać mechanicznego wkuwania wzorów. Lepiej jest zrozumieć, skąd one się biorą.

2. Wzory na pole kwadratu i prostokąta – prosto i skutecznie.

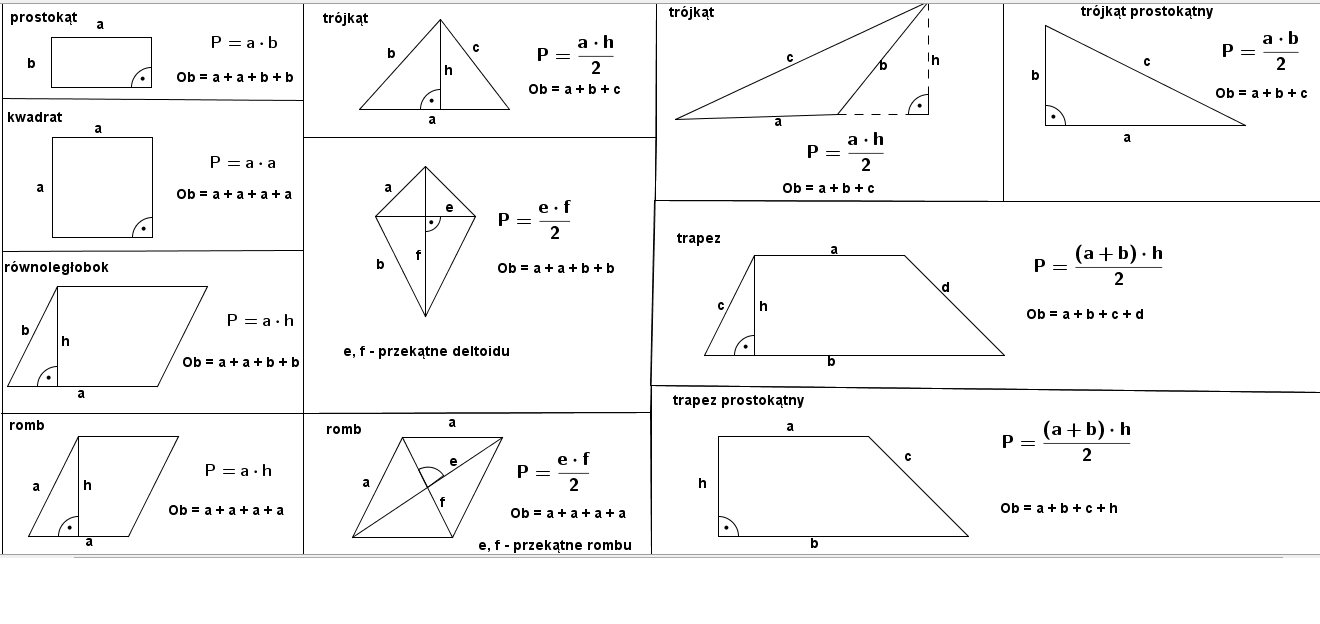
Pole kwadratu: Bok pomnożony przez bok (a * a). Pamiętajmy, że kwadrat ma wszystkie boki równe. Pole prostokąta: Długość pomnożona przez szerokość (a * b). Tutaj boki mogą mieć różne długości.

Warto narysować kilka kwadratów i prostokątów o różnych wymiarach i wspólnie z dzieckiem obliczyć ich pole. Możemy też wykorzystać przedmioty z otoczenia, np. blat stołu, zeszyt, kartkę papieru. Zmierzmy ich boki i obliczmy pole. To pomaga w praktycznym zrozumieniu wzorów.

3. Jednostki pola powierzchni – centymetry, metry i co dalej?

Podobnie jak długość mierzymy w centymetrach, metrach, kilometrach, tak pole powierzchni mierzymy w centymetrach kwadratowych (cm²), metrach kwadratowych (m²), kilometrach kwadratowych (km²). Ważne jest, aby rozumieć różnicę między centymetrem a centymetrem kwadratowym. 1 cm² to pole kwadratu o boku 1 cm.

Możemy pokazać dziecku kwadrat o boku 1 cm i wyjaśnić, że to jest właśnie 1 cm². Następnie możemy narysować kwadrat o boku 1 m (oczywiście w skali) i pokazać, jak duża jest różnica. Ważne jest, aby wizualizować jednostki pola powierzchni.

4. Ćwiczenia, ćwiczenia i jeszcze raz ćwiczenia!

Najlepszym sposobem na utrwalenie wiedzy jest rozwiązywanie zadań. Im więcej zadań rozwiążemy, tym lepiej zrozumiemy zagadnienie i nabierzemy pewności siebie. Możemy korzystać z:

Podręcznika i zeszytu ćwiczeń. Wykorzystajmy wszystkie zadania, które tam znajdziemy.
Zeszytów ćwiczeń dodatkowych. Na rynku jest wiele zeszytów ćwiczeń z matematyki dla klasy 4, które zawierają zadania z pola figur.
Internetu. W Internecie znajdziemy wiele stron z zadaniami z matematyki, w tym z pola figur.
Zadań wymyślonych samodzielnie. Możemy sami wymyślać zadania, np. związane z naszym domem lub ogrodem.

Pamiętajmy, że nie chodzi o to, aby rozwiązać jak najwięcej zadań, ale o to, aby zrozumieć każde zadanie i samodzielnie dojść do poprawnego rozwiązania. Jeśli dziecko ma trudności, pomóżmy mu, ale nie rozwiązujmy zadania za niego. Naprowadźmy je na właściwy tok myślenia, zadawajmy pytania pomocnicze.

5. Zadania tekstowe – klucz do sukcesu.

Zadania tekstowe często sprawiają uczniom najwięcej trudności. Ważne jest, aby nauczyć dziecko, jak analizować treść zadania i wyodrębniać z niej istotne informacje. Możemy stosować następujące kroki:

Przeczytaj uważnie zadanie. Zrozum treść zadania.
Wyodrębnij dane. Zapisz informacje podane w zadaniu.
Zastanów się, co trzeba obliczyć. Ustal, o co pyta zadanie.
Ułóż plan rozwiązania. Zaplanuj, jakie działania trzeba wykonać.
Rozwiąż zadanie. Wykonaj obliczenia.
Sprawdź odpowiedź. Upewnij się, że odpowiedź jest sensowna.

Możemy wymyślać zadania tekstowe związane z sytuacjami z życia codziennego. Na przykład: "Mama chce kupić dywan do pokoju o wymiarach 3 metry na 4 metry. Ile metrów kwadratowych dywanu musi kupić?". To pomaga dziecku zrozumieć, że matematyka ma praktyczne zastosowanie.

6. Wizualizacja i gry edukacyjne.

Wykorzystajmy wizualizacje i gry edukacyjne, aby nauka była bardziej atrakcyjna. Możemy użyć:

Klocków. Klocki mogą pomóc w zrozumieniu pojęcia pola powierzchni. Możemy budować kwadraty i prostokąty z klocków i obliczać ich pole.
Programów komputerowych i aplikacji. Istnieje wiele programów komputerowych i aplikacji, które pomagają w nauce geometrii, w tym pola figur.
Gier planszowych. Możemy wymyślić grę planszową, w której gracze obliczają pole różnych figur.

Pamiętajmy, że nauka przez zabawę jest najskuteczniejsza. Dziecko uczy się szybciej i chętniej, jeśli proces nauki jest dla niego przyjemny.

7. Regularne powtórki i krótkie sesje.

Lepiej uczyć się regularnie, ale krótko, niż długo i sporadycznie. Zalecana jest codzienna, 15-30 minutowa sesja nauki, w której powtarzamy materiał i rozwiązujemy kilka zadań. Regularne powtórki pomagają utrwalić wiedzę i zapobiegają zapominaniu.

8. Pozytywne nastawienie i motywacja.

Ważne jest, aby dziecko miało pozytywne nastawienie do nauki matematyki. Unikajmy mówienia, że matematyka jest trudna i że nikt jej nie lubi. Starajmy się pokazywać dziecku, że matematyka może być ciekawa i przydatna. Chwalmy dziecko za jego wysiłki i postępy, nawet jeśli nie zawsze udaje mu się rozwiązać zadanie poprawnie. Ważne jest, aby dziecko czuło się docenione i zmotywowane do dalszej nauki.

Przykładowe zadania i rozwiązania.

Aby jeszcze lepiej przygotować się do sprawdzianu, przeanalizujmy kilka przykładowych zadań:

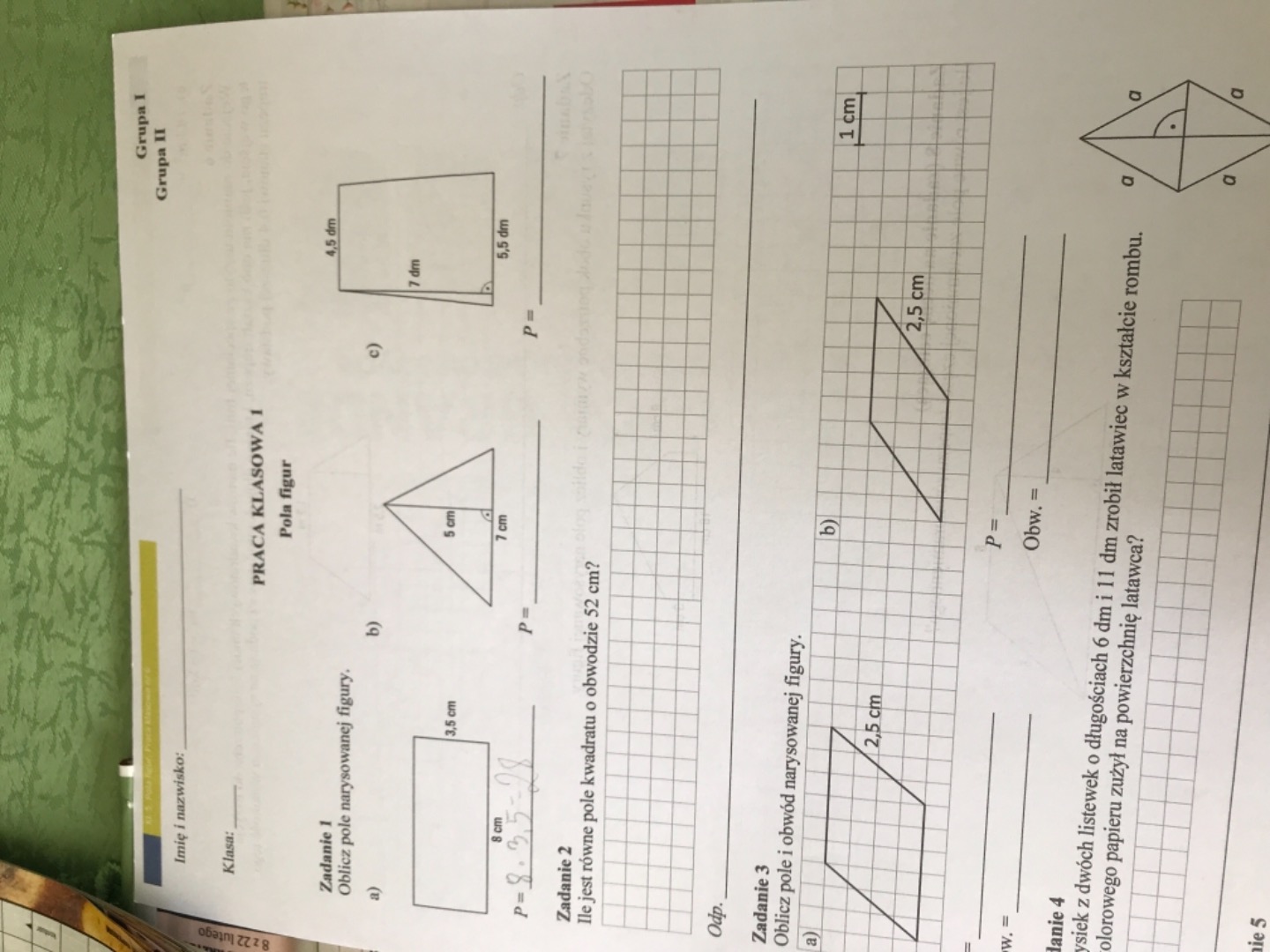
Zadanie 1: Oblicz pole kwadratu o boku 5 cm.

Rozwiązanie: Pole kwadratu = bok * bok = 5 cm * 5 cm = 25 cm²

Zadanie 2: Oblicz pole prostokąta o długości 8 cm i szerokości 3 cm.

Rozwiązanie: Pole prostokąta = długość * szerokość = 8 cm * 3 cm = 24 cm²

Zadanie 3: Pokój ma wymiary 4 m na 5 m. Ile metrów kwadratowych parkietu potrzeba do wyłożenia podłogi?

Rozwiązanie: Pole pokoju = 4 m * 5 m = 20 m². Potrzeba 20 metrów kwadratowych parkietu.

Zadanie 4: Oblicz pole figury, która składa się z dwóch kwadratów o boku 2 cm, połączonych ze sobą.

Rozwiązanie: Pole jednego kwadratu = 2 cm * 2 cm = 4 cm². Pole dwóch kwadratów = 2 * 4 cm² = 8 cm².

Zadanie 5: Porównaj pole kwadratu o boku 6 cm z polem prostokąta o wymiarach 5 cm i 7 cm. Która figura ma większe pole?

Rozwiązanie: Pole kwadratu = 6 cm * 6 cm = 36 cm². Pole prostokąta = 5 cm * 7 cm = 35 cm². Kwadrat ma większe pole.

Podsumowanie i praktyczne wskazówki.

Przygotowanie do sprawdzianu z pola figur w klasie 4 wymaga systematycznej pracy i odpowiedniego podejścia. Pamiętajmy o tym, aby:

Zacząć od podstaw. Upewnijmy się, że dziecko rozumie pojęcie pola powierzchni i jednostek pola.
Utrwalać wzory. Wykorzystujmy praktyczne ćwiczenia i wizualizacje.
Rozwiązywać zadania. Im więcej zadań rozwiążemy, tym lepiej zrozumiemy zagadnienie.
Analizować zadania tekstowe. Nauczmy dziecko, jak wyodrębniać istotne informacje z treści zadania.
Wykorzystywać gry i zabawy edukacyjne. Uczyńmy naukę bardziej atrakcyjną.
Regularnie powtarzać materiał. Unikajmy nauki na ostatnią chwilę.
Motywować dziecko. Chwalmy je za jego wysiłki i postępy.

Pamiętajmy, że sprawdzian to tylko jeden z etapów nauki. Ważniejsze jest, aby dziecko zrozumiało matematykę i polubiło ją. Życzymy powodzenia na sprawdzianie!