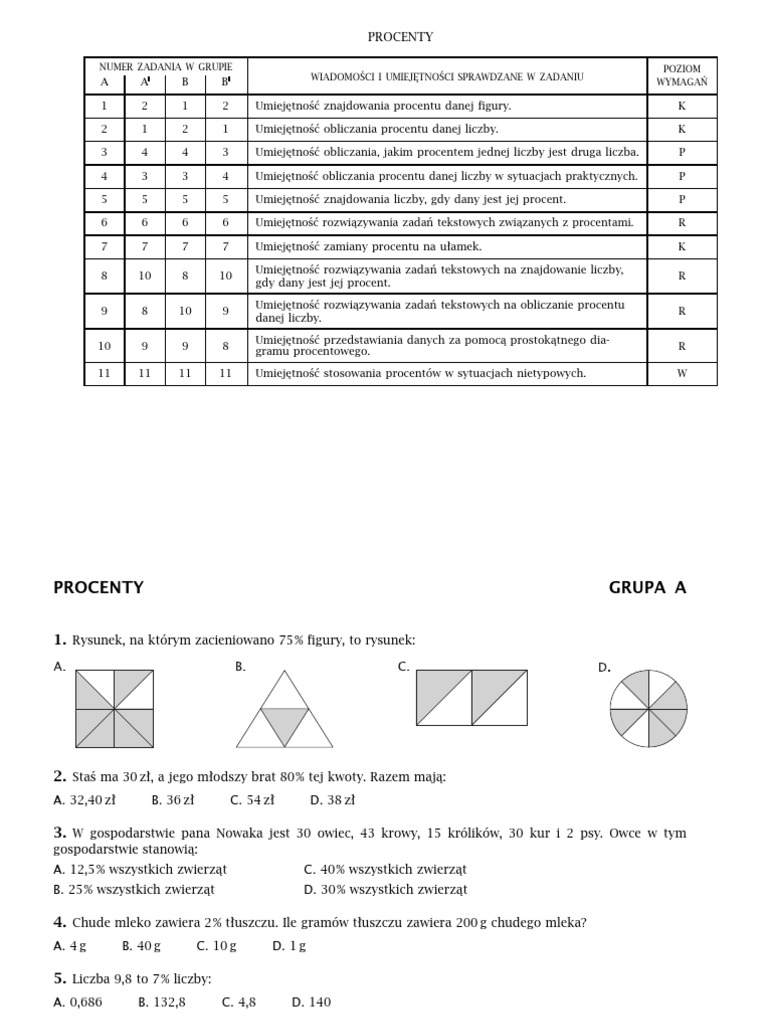
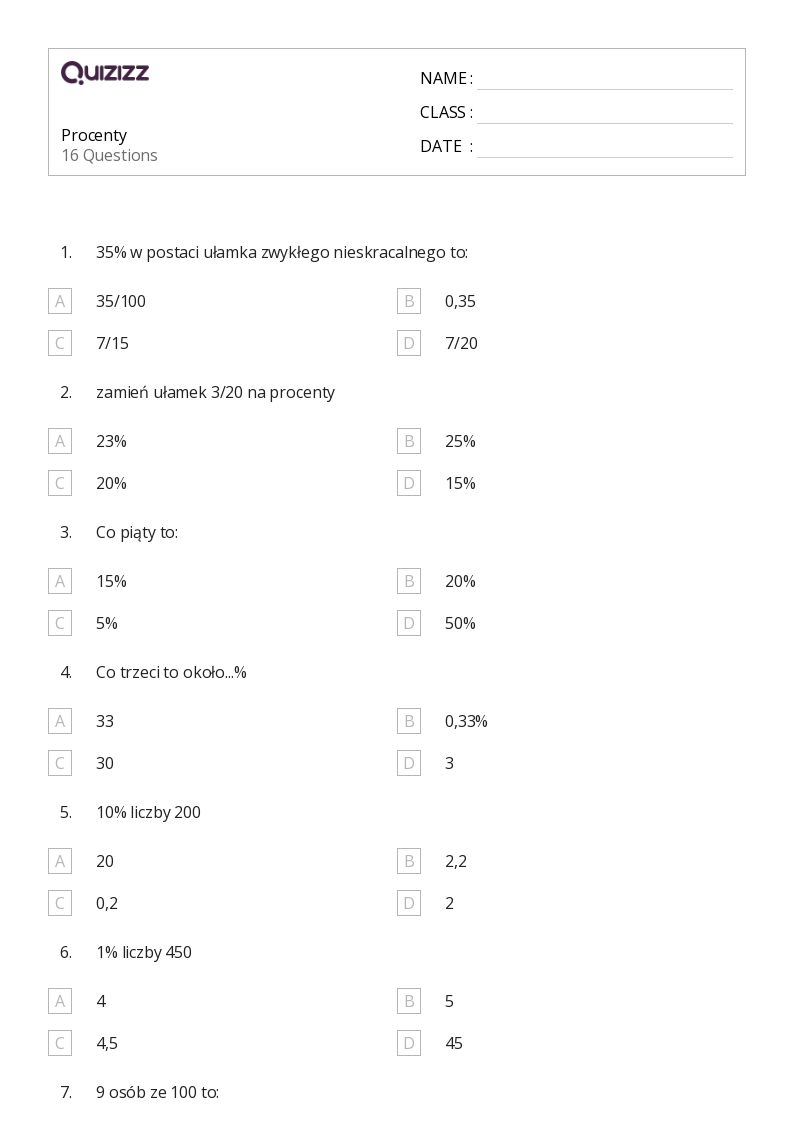
Sprawdzian Z Matematyki Klasa 7 Procenty Odpowiedzi

Hej uczniowie klasy 7! Widzę, że zbliża się sprawdzian z procentów. Spokojnie, pomogę Wam zrozumieć, jak rozwiązywać typowe zadania, które mogą się pojawić. Przejdziemy sobie przez kilka przykładów krok po kroku.

Zacznijmy od podstaw. Procent to po prostu ułamek o mianowniku 100. Oznacza to, że 1% to 1/100, 50% to 50/100 (czyli 1/2), a 100% to 100/100 (czyli 1).

Obliczanie procentu danej liczby

To jest chyba najczęstszy typ zadania. Mamy jakąś liczbę i musimy obliczyć, ile to jest na przykład 20% z tej liczby. Jak to zrobić?

Załóżmy, że mamy liczbę 200 i chcemy obliczyć 20% z tej liczby.

1. Zamieniamy procent na ułamek: 20% to 20/100.
2. Mnożymy liczbę przez ten ułamek: 200 * (20/100).
3. Upraszczamy: Możemy skrócić 20/100 do 1/5.
4. Mnożymy: 200 * (1/5) = 40.

Czyli 20% z 200 to 40.

Kolejny przykład: Oblicz 75% z 80.

1. 75% to 75/100.
2. 80 * (75/100).
3. Skracamy 75/100 do 3/4.
4. 80 * (3/4) = 60.

Zatem 75% z 80 to 60.

Obliczanie, jakim procentem jednej liczby jest druga liczba

Teraz zadanie trochę inne. Mamy dwie liczby i musimy ustalić, jaki procent pierwszej liczby stanowi druga liczba.

Na przykład: Jaki procent liczby 50 stanowi liczba 10?

1. Tworzymy ułamek: Druga liczba (10) podzielona przez pierwszą liczbę (50), czyli 10/50.
2. Skracamy ułamek: 10/50 = 1/5.
3. Zamieniamy ułamek na procent: Mnożymy ułamek przez 100%, czyli (1/5) * 100% = 20%.

Więc liczba 10 stanowi 20% liczby 50.

Inny przykład: Jaki procent liczby 25 stanowi liczba 5?

1. Ułamek: 5/25.
2. Skracamy: 5/25 = 1/5.
3. Mnożymy przez 100%: (1/5) * 100% = 20%.

Odp: 5 stanowi 20% z 25.

Obliczanie liczby, gdy znamy jej procent

To jest trochę trudniejsze, ale damy radę! Mamy informację, że pewna liczba to na przykład 30% jakiejś innej liczby, i musimy znaleźć tę drugą liczbę.

Przykład: 30 to 15% pewnej liczby. Jaka to liczba?

1. Zapisujemy to jako równanie: 15% * x = 30 (gdzie x to szukana liczba).
2. Zamieniamy procent na ułamek: (15/100) * x = 30.
3. Upraszczamy: (3/20) * x = 30.
4. Dzielimy obie strony równania przez (3/20). Pamiętajmy, że dzielenie przez ułamek to to samo, co mnożenie przez jego odwrotność. Czyli mnożymy obie strony przez (20/3).
5. x = 30 * (20/3).
6. x = 200.

Odp: Szukana liczba to 200.

Kolejny przykład: 12 to 25% pewnej liczby. Co to za liczba?

1. Równanie: 25% * x = 12
2. Ułamek: (25/100) * x = 12
3. Upraszczamy: (1/4) * x = 12
4. Mnożymy obie strony przez 4: x = 12 * 4
5. x = 48

Odp: Szukana liczba to 48.

Zadania z podwyżkami i obniżkami

Często na sprawdzianie pojawiają się zadania z cenami, które rosną (podwyżki) lub maleją (obniżki).

Przykład: Cena butów wynosiła 150 zł. Cenę podniesiono o 20%. Ile kosztują buty po podwyżce?

1. Obliczamy kwotę podwyżki: 20% z 150 zł to (20/100) * 150 = 30 zł.
2. Dodajemy kwotę podwyżki do początkowej ceny: 150 zł + 30 zł = 180 zł.

Odp: Buty po podwyżce kosztują 180 zł.

Przykład z obniżką: Cena kurtki wynosiła 200 zł. Cenę obniżono o 15%. Ile kosztuje kurtka po obniżce?

1. Obliczamy kwotę obniżki: 15% z 200 zł to (15/100) * 200 = 30 zł.
2. Odejmujemy kwotę obniżki od początkowej ceny: 200 zł - 30 zł = 170 zł.

Odp: Kurtka po obniżce kosztuje 170 zł.

Zadania z VAT-em

VAT, czyli podatek od towarów i usług, to też procent. Zwykle dodaje się go do ceny netto (czyli ceny bez podatku), żeby uzyskać cenę brutto (czyli cenę, którą płacimy w sklepie).

Przykład: Cena netto towaru wynosi 100 zł. VAT wynosi 23%. Ile wynosi cena brutto?

1. Obliczamy kwotę VAT-u: 23% z 100 zł to (23/100) * 100 = 23 zł.
2. Dodajemy kwotę VAT-u do ceny netto: 100 zł + 23 zł = 123 zł.

Odp: Cena brutto towaru wynosi 123 zł.

Przykład odwrotny: Cena brutto towaru wynosi 123 zł, a VAT wynosi 23%. Ile wynosi cena netto?

To jest trochę trudniejsze, bo nie możemy po prostu odjąć 23% z 123 zł. Musimy to zrobić inaczej.

1. Rozumiemy, że cena brutto (123 zł) to 100% (cena netto) + 23% (VAT), czyli 123% ceny netto.
2. Zapisujemy to jako równanie: 123% * x = 123 (gdzie x to cena netto).
3. Zamieniamy procent na ułamek: (123/100) * x = 123.
4. Dzielimy obie strony równania przez (123/100), czyli mnożymy przez (100/123).
5. x = 123 * (100/123).
6. x = 100.

Odp: Cena netto towaru wynosi 100 zł.

Kilka dodatkowych wskazówek

• Zawsze czytaj uważnie treść zadania! Zastanów się, co jest dane, a co masz obliczyć.
• Zapisuj wszystkie obliczenia krok po kroku. To pomoże Ci uniknąć błędów i sprawdzić, czy dobrze rozumiesz zadanie.
• Jeśli masz trudności z jakimś zadaniem, spróbuj je uprościć. Zamiast obliczać 27% z 345, pomyśl, jak obliczyć 10% z 100.
• Sprawdzaj swoje odpowiedzi! Czy wynik, który otrzymałeś, ma sens w kontekście zadania?
• Pamiętaj, że procenty są wszędzie! W sklepach, w bankach, w wiadomościach. Im lepiej je rozumiesz, tym łatwiej będzie Ci podejmować decyzje w życiu codziennym.

Powodzenia na sprawdzianie! Pamiętaj, że najważniejsze to zrozumieć zasadę działania procentów, a potem po prostu ćwiczyć, ćwiczyć i jeszcze raz ćwiczyć. Im więcej zadań rozwiążesz, tym pewniej będziesz się czuł na sprawdzianie. Trzymam kciuki!