Sprawdzian Z Matematyki Klasa 6 Obliczanie Pola

Czy jesteś gotowy, aby zmierzyć się z tajemnicami pól powierzchni? Sprawdzian z matematyki dla klasy 6, skupiający się na obliczaniu pól, często budzi pewne obawy. Ale bez obaw! Ten artykuł ma na celu rozwiać wszelkie wątpliwości i przygotować Cię do sukcesu. Niezależnie od tego, czy czujesz się pewnie, czy potrzebujesz odświeżenia wiedzy, znajdziesz tutaj cenne wskazówki i praktyczne przykłady.

Co Cię Czeka na Sprawdzianie?

Sprawdzian z obliczania pól w klasie 6 zazwyczaj obejmuje następujące zagadnienia:

• Podstawowe figury geometryczne: Kwadrat, prostokąt, trójkąt, równoległobok, romb, trapez.
• Wzory na pola powierzchni: Musisz znać i rozumieć wzory na obliczanie pól wymienionych figur.
• Zamiana jednostek: Centymetry kwadratowe (cm²), metry kwadratowe (m²), kilometry kwadratowe (km²) i inne.
• Zadania tekstowe: Umiejętność zastosowania wiedzy w praktycznych sytuacjach.
• Figury złożone: Obliczanie pól figur składających się z kilku prostszych figur.

Kluczowe Figury i Wzory: Powtórka Przed Sprawdzianem

Aby solidnie przygotować się do sprawdzianu, odświeżmy sobie wzory na pola podstawowych figur geometrycznych. Pamiętaj, że zrozumienie wzoru jest ważniejsze niż samo jego zapamiętanie!

Kwadrat

Pole kwadratu o boku a: P = a²

Prostokąt

Pole prostokąta o bokach a i b: P = a * b

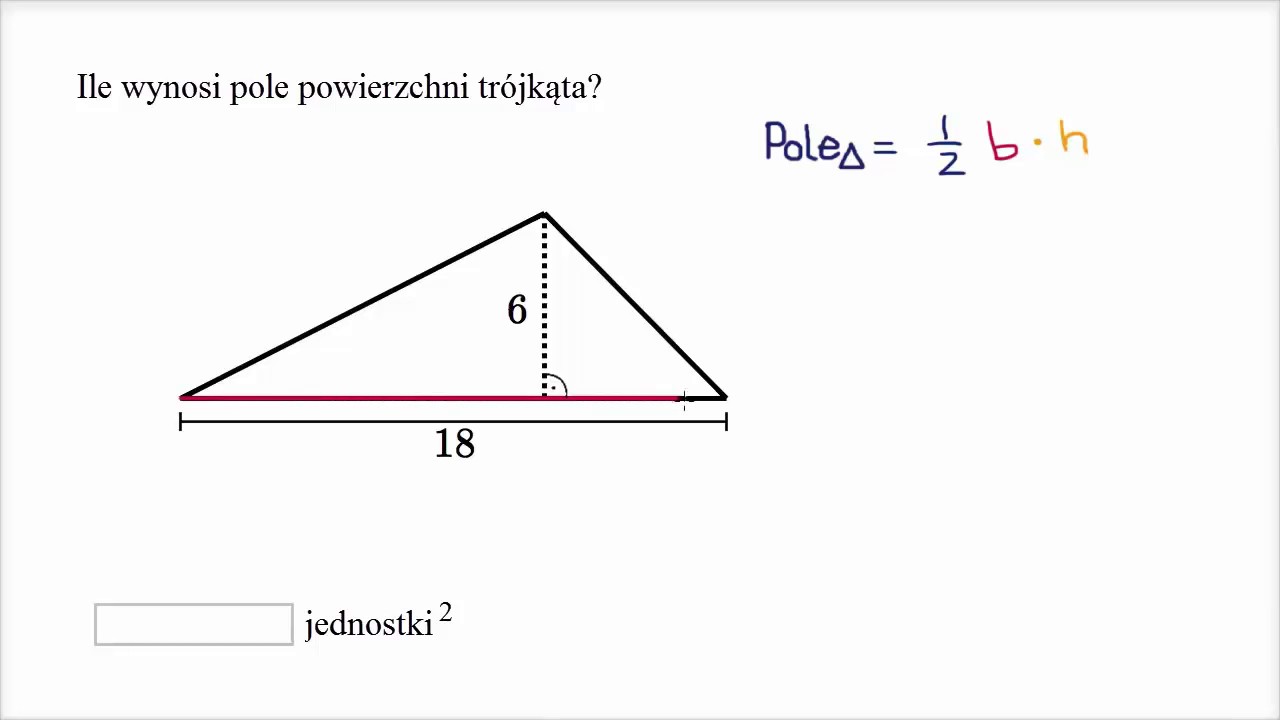
Trójkąt

Pole trójkąta o podstawie a i wysokości h opuszczonej na tę podstawę: P = (a * h) / 2

Równoległobok

Pole równoległoboku o podstawie a i wysokości h opuszczonej na tę podstawę: P = a * h

Romb

Pole rombu o przekątnych e i f: P = (e * f) / 2

Można również obliczyć pole rombu jako równoległoboku: P = a * h, gdzie a to bok rombu, a h to wysokość opuszczona na ten bok.

Trapez

Pole trapezu o podstawach a i b oraz wysokości h: P = ((a + b) * h) / 2

Zamiana Jednostek: Uniknij Pułapek!

Pamiętaj, że przy obliczaniu pól bardzo ważne jest, aby wszystkie wymiary były podane w tych samych jednostkach! Jeśli masz długość w metrach i szerokość w centymetrach, musisz je najpierw ujednolicić. Oto kilka przydatnych przeliczeń:

• 1 m = 100 cm
• 1 cm = 10 mm
• 1 km = 1000 m
• 1 m² = 10000 cm²

Przykład: Oblicz pole prostokąta o długości 2 m i szerokości 50 cm. Zanim zaczniesz obliczać pole, zamień 50 cm na metry: 50 cm = 0,5 m. Teraz możesz obliczyć pole: P = 2 m * 0,5 m = 1 m².

Zadania Tekstowe: Czytanie ze Zrozumieniem to Klucz

Zadania tekstowe często sprawiają najwięcej problemów. Kluczem do sukcesu jest uważne czytanie ze zrozumieniem! Wyodrębnij najważniejsze informacje, zidentyfikuj, co masz obliczyć, i zastanów się, jakie wzory będą potrzebne.

Przykład: Pokój ma kształt prostokąta o wymiarach 4 m na 3 m. Ile metrów kwadratowych wykładziny potrzeba, aby pokryć całą podłogę?

Rozwiązanie: Pole prostokąta (podłogi) obliczamy: P = 4 m * 3 m = 12 m². Odpowiedź: Potrzeba 12 m² wykładziny.

Figury Złożone: Rozbij Problem na Mniejsze Części

Gdy masz do czynienia z figurą złożoną, podziel ją na prostsze figury, których pola potrafisz obliczyć. Następnie dodaj pola tych figur, aby uzyskać pole całej figury.

Przykład: Wyobraź sobie figurę w kształcie litery L. Możesz ją podzielić na dwa prostokąty. Oblicz pole każdego prostokąta oddzielnie, a następnie dodaj je do siebie.

Praktyczne Porady na Sprawdzian

• Przed sprawdzianem: Rozwiąż jak najwięcej zadań z podręcznika i zbiorów zadań.
• W trakcie sprawdzianu: Przeczytaj uważnie każde zadanie. Zaznacz najważniejsze informacje.
• Zapisuj obliczenia: Nawet jeśli znasz odpowiedź od razu, zapisz swoje obliczenia. Ułatwi to nauczycielowi sprawdzenie Twojej pracy, a Tobie uniknięcie błędów.
• Sprawdzaj jednostki: Upewnij się, że wszystkie wymiary są w tych samych jednostkach.
• Sprawdź wynik: Czy wynik jest realny? Czy ma sens w kontekście zadania?

Pamiętaj, że ćwiczenie czyni mistrza! Im więcej zadań rozwiążesz, tym pewniej poczujesz się na sprawdzianie. Powodzenia!

Podsumowanie

Przygotowanie do sprawdzianu z obliczania pól to inwestycja w Twoją wiedzę i umiejętności matematyczne. Mamy nadzieję, że ten artykuł pomoże Ci z sukcesem zmierzyć się z tym wyzwaniem. Powodzenia na sprawdzianie! Pamiętaj, dasz radę!