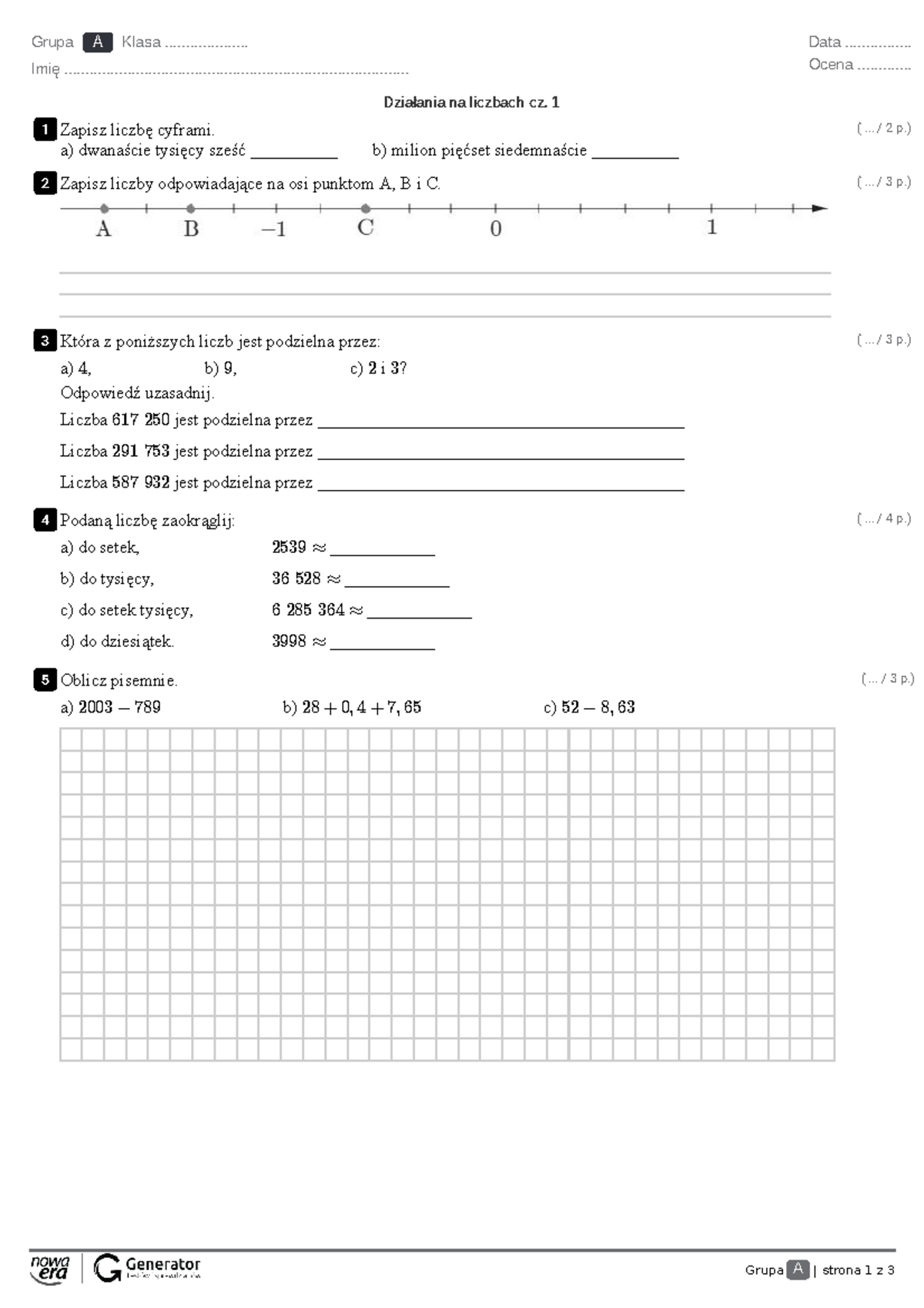
Sprawdzian Z Matematyki Klasa 6 Działania Na Liczbach Część 2

Okej, rozważmy sprawdzian z matematyki dla klasy 6, dział dotyczący działań na liczbach, część 2. Postaram się wytłumaczyć to najprościej, jak potrafię. Pamiętaj, że ćwiczenie czyni mistrza, więc im więcej przykładów rozwiążesz, tym łatwiej będzie Ci na sprawdzianie.

Zacznijmy od podstaw.

Kolejność wykonywania działań

Pamiętaj, co robimy najpierw:

1. Nawiasy: Wszystko, co jest w nawiasach, robimy jako pierwsze.
2. Potęgowanie i pierwiastkowanie: Jeśli masz potęgi lub pierwiastki, to one są następne w kolejce. (W klasie 6 często nie ma jeszcze pierwiastków, ale potęgi mogą się pojawić).
3. Mnożenie i dzielenie: Wykonujemy od lewej do prawej.
4. Dodawanie i odejmowanie: Wykonujemy od lewej do prawej.

Przykład:

2 + 3 * 4 = ?

Najpierw mnożymy: 3 * 4 = 12

Potem dodajemy: 2 + 12 = 14

Odp: 14

Przykład z nawiasem:

(2 + 3) * 4 = ?

Najpierw dodajemy w nawiasie: 2 + 3 = 5

Potem mnożymy: 5 * 4 = 20

Odp: 20

Widzisz różnicę? Nawias zmienia kolejność!

Ułamki

Ułamki mogą wydawać się trudne, ale z odrobiną praktyki staną się proste.

Dodawanie i odejmowanie ułamków:

Żeby dodać lub odjąć ułamki, muszą mieć wspólny mianownik. Czyli liczba na dole ułamka musi być taka sama.

Przykład:

1/2 + 1/4 = ?

Mianowniki to 2 i 4. Wspólny mianownik to 4. Ułamek 1/2 musimy "rozszerzyć" żeby miał mianownik 4. Robimy to mnożąc licznik i mianownik przez tę samą liczbę. W tym przypadku przez 2.

(1 * 2) / (2 * 2) = 2/4

Teraz mamy:

2/4 + 1/4 = ?

Dodajemy liczniki (górne liczby), a mianownik zostaje ten sam:

(2 + 1) / 4 = 3/4

Odp: 3/4

Przykład z odejmowaniem:

3/5 - 1/5 = ?

Mianowniki są takie same, więc odejmujemy liczniki:

(3 - 1) / 5 = 2/5

Odp: 2/5

A co, jeśli mianowniki są różne? Musimy znaleźć wspólny mianownik. Często można go znaleźć mnożąc mianowniki przez siebie, ale czasem można znaleźć mniejszy wspólny mianownik.

Przykład:

1/3 + 1/6 = ?

Mianowniki to 3 i 6. Możemy pomnożyć 3 * 6 = 18, ale 6 jest wielokrotnością 3. Więc 6 jest wspólnym mianownikiem. Rozszerzamy ułamek 1/3, mnożąc licznik i mianownik przez 2.

(1 * 2) / (3 * 2) = 2/6

Teraz mamy:

2/6 + 1/6 = 3/6

Możemy jeszcze skrócić ułamek 3/6 dzieląc licznik i mianownik przez 3.

(3 / 3) / (6 / 3) = 1/2

Odp: 1/2

Mnożenie ułamków:

Mnożenie ułamków jest proste! Mnożymy licznik przez licznik i mianownik przez mianownik.

Przykład:

1/2 * 2/3 = ?

(1 * 2) / (2 * 3) = 2/6

Możemy skrócić 2/6, dzieląc licznik i mianownik przez 2.

(2 / 2) / (6 / 2) = 1/3

Odp: 1/3

Dzielenie ułamków:

Dzielenie ułamków to tak naprawdę mnożenie przez odwrotność drugiego ułamka. Odwrotność ułamka to zamiana licznika z mianownikiem.

Przykład:

1/2 : 2/3 = ?

Odwrotność 2/3 to 3/2. Zamiast dzielić, mnożymy:

1/2 * 3/2 = ?

(1 * 3) / (2 * 2) = 3/4

Odp: 3/4

Liczby mieszane

Liczba mieszana to liczba, która ma część całkowitą i ułamek. Na przykład 2 1/2 (dwa i jedna druga).

Zamiana liczby mieszanej na ułamek niewłaściwy:

Żeby zamienić liczbę mieszaną na ułamek niewłaściwy (gdzie licznik jest większy od mianownika), robimy tak:

1. Mnożymy część całkowitą przez mianownik ułamka.
2. Dodajemy wynik do licznika ułamka.
3. Mianownik zostaje ten sam.

Przykład:

2 1/2 = ?

1. 2 * 2 = 4
2. 4 + 1 = 5
3. Mianownik to 2.

Więc 2 1/2 = 5/2

Dodawanie i odejmowanie liczb mieszanych:

Można to robić na dwa sposoby:

1. Zamienić liczby mieszane na ułamki niewłaściwe, a potem dodać lub odjąć ułamki.
2. Dodać lub odjąć części całkowite oddzielnie i ułamki oddzielnie. Jeśli przy odejmowaniu ułamka brakuje, pożyczamy 1 z części całkowitej zamieniając ją na ułamek.

Przykład (sposób 1):

1 1/4 + 2 1/2 = ?

Zamieniamy na ułamki niewłaściwe:

1 1/4 = 5/4

2 1/2 = 5/2 = 10/4

Teraz dodajemy:

5/4 + 10/4 = 15/4

Możemy to zamienić z powrotem na liczbę mieszaną:

15/4 = 3 3/4

Przykład (sposób 2):

3 1/3 - 1 2/3 = ?

Odejmujemy części całkowite: 3 - 1 = 2

Odejmujemy ułamki: 1/3 - 2/3 = ? Nie możemy odjąć 2/3 od 1/3. Pożyczamy 1 z części całkowitej, zamieniając ją na 3/3.

Teraz mamy: 2 + 1 1/3 - 1 2/3 = 2 + 4/3 - 1 2/3

Odejmujemy części całkowite: 2 - 1 = 1

Odejmujemy ułamki: 4/3 - 2/3 = 2/3

Więc wynik to: 1 2/3

Mnożenie i dzielenie liczb mieszanych:

Najprościej jest zamienić liczby mieszane na ułamki niewłaściwe i wtedy mnożyć lub dzielić jak zwykłe ułamki.

Działania na liczbach dziesiętnych

Liczby dziesiętne to po prostu liczby z przecinkiem.

Dodawanie i odejmowanie liczb dziesiętnych:

Najważniejsze jest, żeby ustawić przecinki jeden pod drugim. Wtedy dodajemy lub odejmujemy jak zwykłe liczby.

Przykład:

2,5 + 1,75 = ?

  2,50
+ 1,75
-------
  4,25

Odp: 4,25

Mnożenie liczb dziesiętnych:

Mnożymy jak zwykłe liczby, ignorując przecinek. Potem liczymy, ile cyfr jest po przecinku w obu liczbach razem. W wyniku odliczamy tyle cyfr od prawej strony i stawiamy przecinek.

Przykład:

1,2 * 0,5 = ?

12 * 5 = 60

W 1,2 jest jedna cyfra po przecinku. W 0,5 jest jedna cyfra po przecinku. Razem to dwie cyfry.

Odliczamy dwie cyfry od prawej w 60 i stawiamy przecinek: 0,60.

Odp: 0,60 (czyli 0,6)

Dzielenie liczb dziesiętnych:

Jeśli dzielimy liczbę dziesiętną przez liczbę całkowitą, dzielimy normalnie, a przecinek w wyniku stawiamy w tym samym miejscu, co w dzielnej.

Przykład:

6,4 : 2 = ?

6 : 2 = 3

4 : 2 = 2

Więc 6,4 : 2 = 3,2

Jeśli dzielimy przez liczbę dziesiętną, musimy przesunąć przecinek w obu liczbach (dzielnej i dzielniku) o tyle miejsc w prawo, żeby dzielnik stał się liczbą całkowitą.

Przykład:

1,5 : 0,3 = ?

Przesuwamy przecinek o jedno miejsce w prawo w obu liczbach:

15 : 3 = 5

Odp: 5

Pamiętaj! Ćwicz, ćwicz i jeszcze raz ćwicz! Im więcej zadań rozwiążesz, tym pewniej poczujesz się na sprawdzianie. Powodzenia!