Sprawdzian Z Matematyki Klasa 5 Własności Liczb Naturalnych

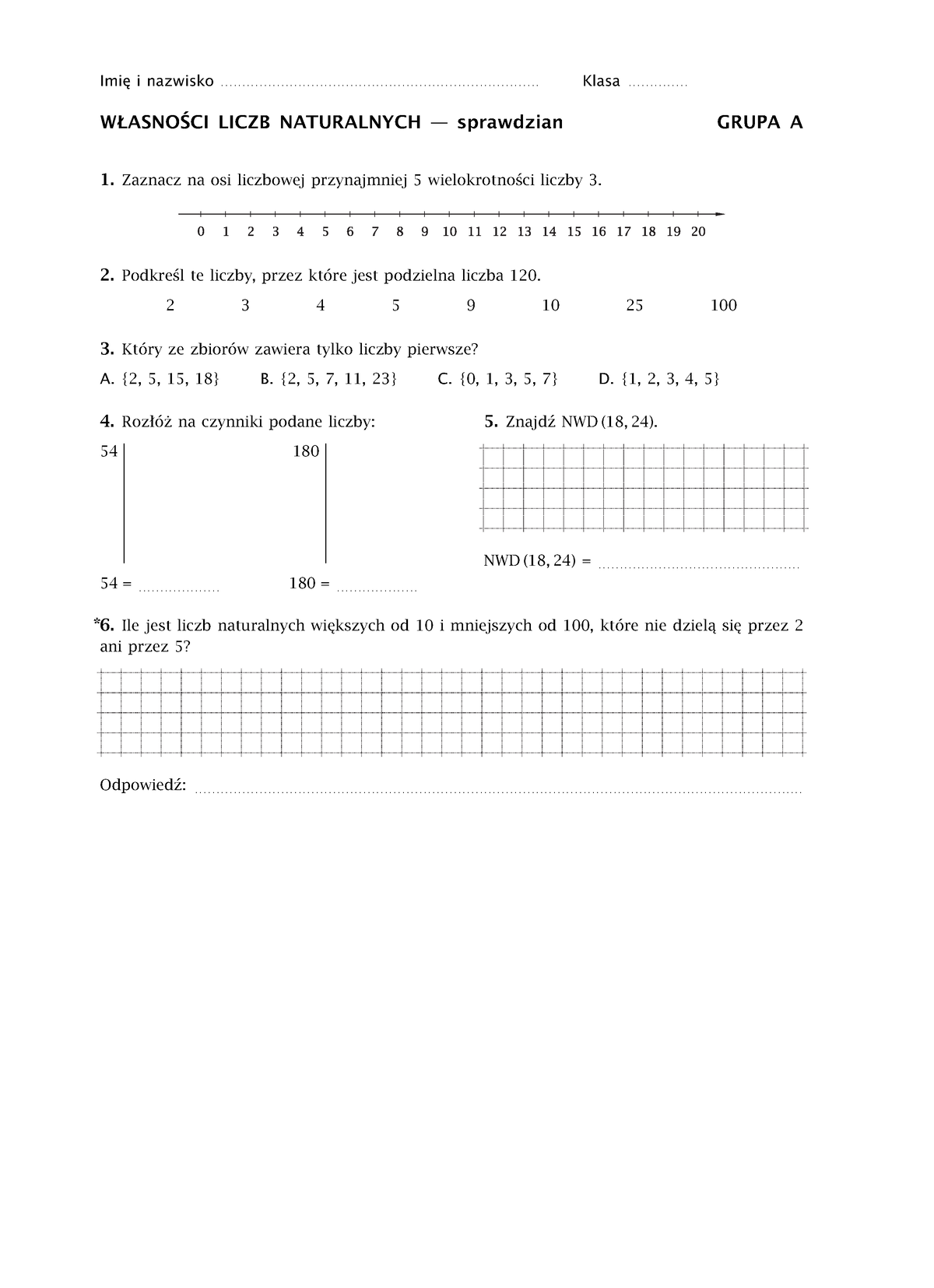
Sprawdzian z matematyki w piątej klasie to często pierwszy poważny test wiedzy matematycznej. Dział dotyczący własności liczb naturalnych jest fundamentem, na którym buduje się dalszą edukację matematyczną. Opanowanie go jest kluczowe dla sukcesu w kolejnych etapach nauki.

Zacznijmy od podstaw, czyli definicji. Liczby naturalne to liczby całkowite, nieujemne, służące do liczenia: 0, 1, 2, 3, i tak dalej w nieskończoność. Ważne jest, by pamiętać, że zero jest liczbą naturalną, choć bywa to kwestią umowną w różnych kontekstach.

Podzielność liczb naturalnych to jedno z ważniejszych zagadnień. Mówimy, że liczba a jest podzielna przez liczbę b (gdzie b jest różne od zera), jeśli istnieje taka liczba całkowita c, że a = b * c. Na przykład, 12 jest podzielne przez 3, ponieważ 12 = 3 * 4.

Sprawdzian często sprawdza znajomość cech podzielności. Znajomość tych zasad znacząco ułatwia rozwiązywanie zadań.

Podzielność przez 2: Liczba jest podzielna przez 2, jeśli jej ostatnia cyfra jest parzysta (0, 2, 4, 6, 8). Na przykład, 124 jest podzielne przez 2, ponieważ ostatnia cyfra to 4.
Podzielność przez 3: Liczba jest podzielna przez 3, jeśli suma jej cyfr jest podzielna przez 3. Na przykład, 345 jest podzielne przez 3, ponieważ 3 + 4 + 5 = 12, a 12 jest podzielne przez 3.
Podzielność przez 4: Liczba jest podzielna przez 4, jeśli liczba utworzona przez jej dwie ostatnie cyfry jest podzielna przez 4. Na przykład, 1316 jest podzielne przez 4, ponieważ 16 jest podzielne przez 4.
Podzielność przez 5: Liczba jest podzielna przez 5, jeśli jej ostatnia cyfra to 0 lub 5. Na przykład, 235 jest podzielne przez 5, ponieważ ostatnia cyfra to 5.
Podzielność przez 9: Liczba jest podzielna przez 9, jeśli suma jej cyfr jest podzielna przez 9. Na przykład, 819 jest podzielne przez 9, ponieważ 8 + 1 + 9 = 18, a 18 jest podzielne przez 9.
Podzielność przez 10: Liczba jest podzielna przez 10, jeśli jej ostatnia cyfra to 0. Na przykład, 450 jest podzielne przez 10, ponieważ ostatnia cyfra to 0.

Kolejnym ważnym pojęciem są liczby pierwsze i liczby złożone. Liczba pierwsza to liczba naturalna większa od 1, która ma dokładnie dwa dzielniki: 1 i samą siebie. Przykłady liczb pierwszych to: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29. Liczba złożona to liczba naturalna większa od 1, która ma więcej niż dwa dzielniki. Przykłady liczb złożonych to: 4, 6, 8, 9, 10, 12, 14, 15, 16, 18. Liczba 1 nie jest ani liczbą pierwszą, ani liczbą złożoną.

Rozkład liczby na czynniki pierwsze to przedstawienie jej w postaci iloczynu liczb pierwszych. Jest to bardzo przydatna umiejętność przy wielu zadaniach. Przykładowo, rozkład liczby 60 na czynniki pierwsze to: 60 = 2 * 2 * 3 * 5 = 2² * 3 * 5. Rozkład na czynniki pierwsze można wykonać za pomocą drzewka dzielników lub po prostu dzieląc liczbę kolejno przez najmniejsze liczby pierwsze (2, 3, 5, 7, 11, …) aż do uzyskania 1.

Znajdowanie największego wspólnego dzielnika (NWD) i najmniejszej wspólnej wielokrotności (NWW) to kolejne kluczowe umiejętności. NWD dwóch lub więcej liczb to największa liczba, która dzieli wszystkie te liczby bez reszty. NWW dwóch lub więcej liczb to najmniejsza liczba, która jest podzielna przez wszystkie te liczby.

Obliczanie NWD i NWW

NWD i NWW można obliczyć na kilka sposobów. Jednym z nich jest wykorzystanie rozkładu liczb na czynniki pierwsze.

Aby znaleźć NWD, należy wypisać rozkłady wszystkich liczb na czynniki pierwsze, a następnie wybrać czynniki pierwsze, które występują we wszystkich rozkładach z najmniejszą potęgą, w jakiej występują. Iloczyn tych czynników to NWD. Na przykład, NWD(24, 36) obliczamy następująco: 24 = 2³ * 3 36 = 2² * 3² NWD(24, 36) = 2² * 3 = 12

Aby znaleźć NWW, należy wypisać rozkłady wszystkich liczb na czynniki pierwsze, a następnie wybrać wszystkie czynniki pierwsze, które występują w co najmniej jednym rozkładzie z największą potęgą, w jakiej występują. Iloczyn tych czynników to NWW. Na przykład, NWW(24, 36) obliczamy następująco: 24 = 2³ * 3 36 = 2² * 3² NWW(24, 36) = 2³ * 3² = 72

Inną metodą obliczania NWD jest algorytm Euklidesa. Polega on na powtarzaniu operacji dzielenia z resztą, aż do uzyskania reszty równej zero. Ostatnia niezerowa reszta jest NWD. Na przykład, NWD(48, 18) obliczamy następująco: 48 = 2 * 18 + 12 18 = 1 * 12 + 6 12 = 2 * 6 + 0 NWD(48, 18) = 6

Własności działań na liczbach naturalnych to również istotny element sprawdzianu. Należy pamiętać o przemienności, łączności i rozdzielności działań.

Przemienność dodawania: a + b = b + a. Kolejność dodawania nie ma znaczenia.
Przemienność mnożenia: a * b = b * a. Kolejność mnożenia nie ma znaczenia.
Łączność dodawania: (a + b) + c = a + (b + c). Kolejność wykonywania dodawania przy więcej niż dwóch liczbach nie ma znaczenia.
Łączność mnożenia: (a * b) * c = a * (b * c). Kolejność wykonywania mnożenia przy więcej niż dwóch liczbach nie ma znaczenia.
Rozdzielność mnożenia względem dodawania: a * (b + c) = a * b + a * c. Mnożenie można "rozdzielić" na dodawanie.
Rozdzielność mnożenia względem odejmowania: a * (b - c) = a * b - a * c. Mnożenie można "rozdzielić" na odejmowanie.

Kolejność wykonywania działań to absolutna podstawa. Najpierw wykonujemy działania w nawiasach, następnie potęgowanie i pierwiastkowanie (jeśli występują), potem mnożenie i dzielenie (od lewej do prawej), a na końcu dodawanie i odejmowanie (również od lewej do prawej). Pamiętanie o tej kolejności jest kluczowe, by uniknąć błędów w obliczeniach.

Praktyczne zadania, w których trzeba zastosować wiedzę o własnościach liczb naturalnych, to częsty element sprawdzianu. Mogą to być zadania tekstowe, zadania na obliczanie pól i obwodów figur geometrycznych, zadania na dzielenie z resztą, czy zadania na szukanie NWD i NWW.

Przykładowe zadanie:

"Janek ma 24 jabłka i 36 gruszek. Chce podzielić owoce pomiędzy swoich kolegów tak, aby każdy kolega otrzymał tyle samo jabłek i tyle samo gruszek, a wszystkie owoce zostały rozdane. Ilu najwięcej kolegów może obdarować Janek?"

Rozwiązanie:

Szukamy NWD(24, 36), który wynosi 12. Janek może obdarować najwięcej 12 kolegów. Każdy kolega otrzyma 2 jabłka i 3 gruszki.

Inny przykład:

"Dwa autobusy wyjeżdżają z tego samego przystanku o godzinie 8:00. Jeden autobus wraca na ten przystanek co 30 minut, a drugi co 45 minut. O której godzinie autobusy spotkają się ponownie na przystanku?"

Rozwiązanie:

Szukamy NWW(30, 45). 30 = 2 * 3 * 5 45 = 3² * 5 NWW(30, 45) = 2 * 3² * 5 = 90 Autobusy spotkają się ponownie na przystanku po 90 minutach, czyli o 9:30.

Systematyczna praca i rozwiązywanie zadań to najlepszy sposób na przygotowanie się do sprawdzianu. Warto regularnie powtarzać materiał, rozwiązywać zadania z podręcznika i zeszytu ćwiczeń, a także korzystać z dodatkowych źródeł, takich jak zbiory zadań czy platformy edukacyjne online.

Dobrym pomysłem jest również rozwiązywanie testów i sprawdzianów z poprzednich lat. Pozwoli to oswoić się z formą sprawdzianu i typami zadań, które mogą się na nim pojawić.

Nie należy bać się pytać nauczyciela o rzeczy, które są niezrozumiałe. Lepiej wyjaśnić wątpliwości na bieżąco, niż zostawić je na ostatnią chwilę.

Pamiętaj, że sukces na sprawdzianie zależy przede wszystkim od Twojej pracy i zaangażowania. Im więcej czasu poświęcisz na naukę i rozwiązywanie zadań, tym większa szansa na to, że uzyskasz dobry wynik. Powodzenia!