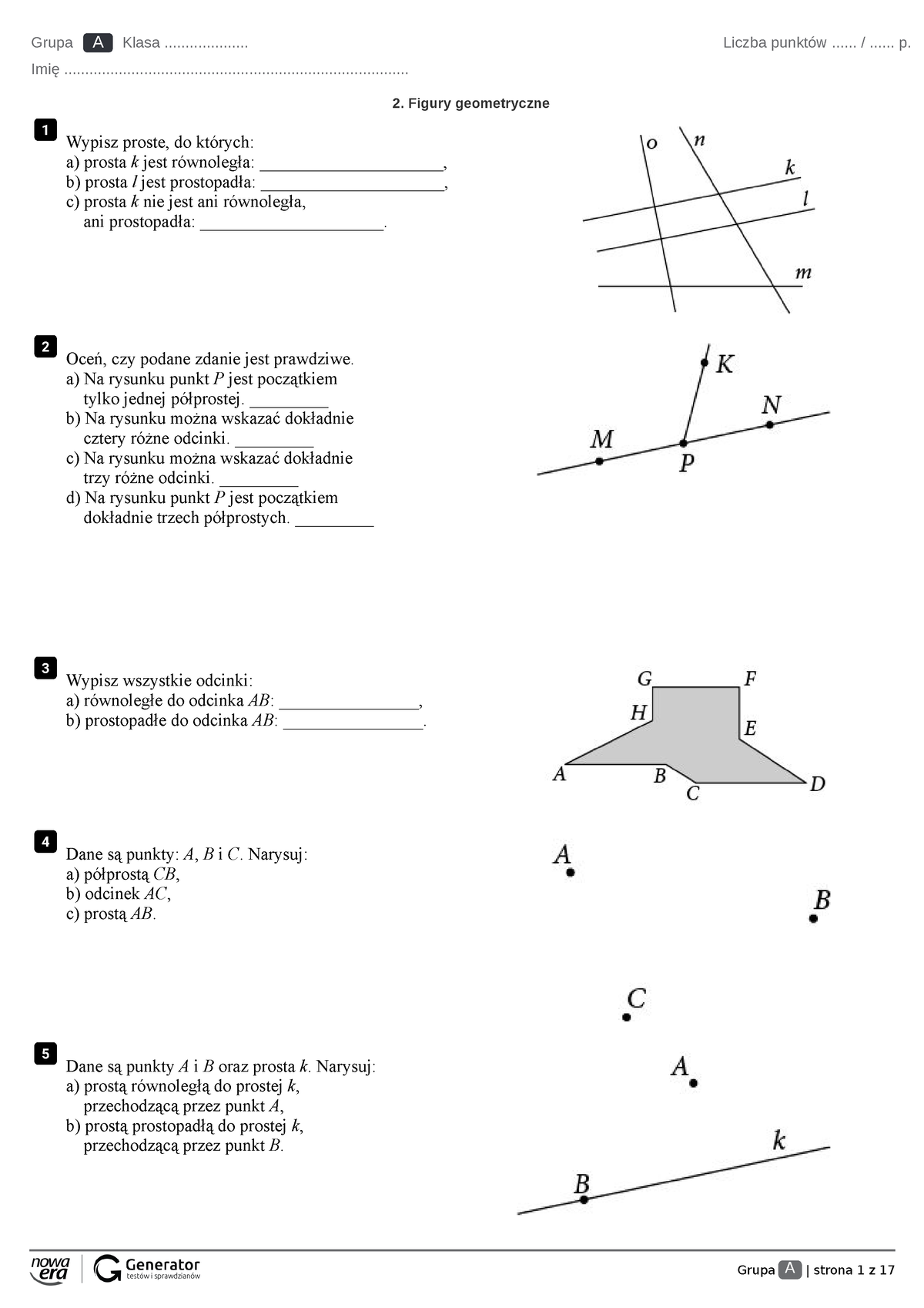
Sprawdzian Z Matematyki Klasa 5 Figury Geometryczne Nowa Era

Hej dzieciaki! Widzę, że zbliża się sprawdzian z figur geometrycznych w klasie 5 z Nowej Ery i macie trochę pytań. Super! Postaram się wam wszystko wyjaśnić tak prosto, jak tylko potrafię, żebyście na sprawdzianie zabłysnęli wiedzą!

Zacznijmy od podstaw. Musimy dobrze znać nazwy figur i ich cechy.

Podstawowe figury geometryczne na płaszczyźnie

Pamiętajcie, że mówimy teraz o figurach, które możemy narysować na kartce. To ważne!

Punkt: Punkt to po prostu kropka. Nie ma żadnego rozmiaru, tylko położenie. Oznaczamy go dużą literą, na przykład punkt A.
Prosta: Prosta to linia, która nie ma początku ani końca. Ciągnie się w nieskończoność w obie strony. Możemy przez nią narysować strzałki na końcach, żeby to pokazać. Oznaczamy ją małymi literami, np. prosta k, albo dwoma punktami, które na niej leżą, np. prosta AB.
Odcinek: Odcinek to część prostej, która ma początek i koniec. Jest ograniczony dwoma punktami. Oznaczamy go dwoma punktami, które są jego końcami, np. odcinek AB. Pamiętajcie, że kolejność liter nie ma znaczenia, odcinek AB to to samo co odcinek BA.
Półprosta: Półprosta to część prostej, która ma początek, ale nie ma końca. Ma jeden punkt początkowy i ciągnie się w nieskończoność w jednym kierunku. Oznaczamy ją tak jak prostą, ale kolejność liter jest ważna! Najpierw piszemy literę oznaczającą punkt początkowy, a potem dowolny inny punkt na półprostej. Np. półprosta AB.
Kąt: Kąt to figura, która powstaje, gdy dwie półproste mają wspólny początek. Ten punkt nazywamy wierzchołkiem kąta, a półproste to ramiona kąta. Mierzymy kąty w stopniach. Kąty oznaczamy trzema literami (wierzchołek w środku), np. kąt ABC, albo greckimi literami, np. kąt α (alfa).

Rodzaje kątów:

Kąt prosty: Ma 90 stopni. Wygląda jak róg kartki. Często oznaczamy go małym kwadracikiem w rogu.
Kąt ostry: Ma mniej niż 90 stopni. Jest mniejszy od kąta prostego.
Kąt rozwarty: Ma więcej niż 90 stopni, ale mniej niż 180 stopni. Jest większy od kąta prostego, ale mniejszy od kąta półpełnego.
Kąt półpełny: Ma 180 stopni. Wygląda jak prosta.
Kąt pełny: Ma 360 stopni. To cały okrąg.

Wielokąty

Wielokąt to figura, która jest ograniczona odcinkami. Te odcinki to boki wielokąta.

Trójkąt: Ma 3 boki i 3 kąty.
Czworokąt: Ma 4 boki i 4 kąty.
Pięciokąt: Ma 5 boków i 5 kątów.
Sześciokąt: Ma 6 boków i 6 kątów.

I tak dalej…

Rodzaje trójkątów:

Trójkąt równoboczny: Ma wszystkie boki równe i wszystkie kąty równe (po 60 stopni).
Trójkąt równoramienny: Ma dwa boki równe (ramiona). Kąty przy podstawie (trzeci bok) są równe.
Trójkąt różnoboczny: Ma wszystkie boki różnej długości i wszystkie kąty różnej miary.
Trójkąt prostokątny: Ma jeden kąt prosty.
Trójkąt ostrokątny: Ma wszystkie kąty ostre.
Trójkąt rozwartokątny: Ma jeden kąt rozwarty.

Rodzaje czworokątów:

Kwadrat: Ma wszystkie boki równe i wszystkie kąty proste.
Prostokąt: Ma wszystkie kąty proste, ale boki mogą mieć różne długości (przeciwległe boki są równe).
Romb: Ma wszystkie boki równe, ale kąty nie muszą być proste. Przeciwległe kąty są równe.
Równoległobok: Ma przeciwległe boki równoległe i równe. Przeciwległe kąty są równe.
Trapez: Ma przynajmniej jedną parę boków równoległych (podstawy).

Obwód i pole

Obwód: To suma długości wszystkich boków figury. Musimy dodać do siebie długości wszystkich boków. Pamiętajcie o jednostkach! Jak mamy boki w centymetrach, to obwód też będzie w centymetrach.
Pole: To ilość miejsca, jaką zajmuje figura na płaszczyźnie. Pole liczymy, używając wzorów. Pole podajemy w jednostkach kwadratowych, np. cm², m², km².

Wzory na pola:

Kwadrat: Pole = bok * bok (a²)
Prostokąt: Pole = bok * bok (a * b)
Trójkąt: Pole = (podstawa * wysokość) / 2 ( (a * h) / 2) (Wysokość to odcinek prostopadły do podstawy, poprowadzony z wierzchołka naprzeciwko podstawy)
Równoległobok: Pole = podstawa * wysokość (a * h) (Wysokość to odcinek prostopadły do podstawy, poprowadzony z wierzchołka naprzeciwko podstawy)
Romb: Pole = (przekątna * przekątna) / 2 ( (e * f) / 2) (Przekątne to odcinki łączące przeciwległe wierzchołki)
Trapez: Pole = ((podstawa + podstawa) * wysokość) / 2 (((a + b) * h) / 2) (a i b to długości podstaw, h to wysokość)

Figury przestrzenne

Teraz przejdziemy do figur, które nie są płaskie, ale mają trzy wymiary: długość, szerokość i wysokość.

Sześcian: Ma wszystkie ściany kwadratowe. Ma 6 ścian, 12 krawędzi i 8 wierzchołków.
Prostopadłościan: Ma wszystkie ściany prostokątne. Ma 6 ścian, 12 krawędzi i 8 wierzchołków. Sześcian to szczególny przypadek prostopadłościanu.
Graniastosłup: Ma dwie podstawy, które są identycznymi wielokątami, i ściany boczne, które są prostokątami. Nazwa graniastosłupa pochodzi od kształtu jego podstawy, np. graniastosłup trójkątny, graniastosłup pięciokątny.
Ostrosłup: Ma jedną podstawę (wielokąt) i ściany boczne, które są trójkątami, zbiegającymi się w jednym punkcie (wierzchołku ostrosłupa). Nazwa ostrosłupa pochodzi od kształtu jego podstawy, np. ostrosłup trójkątny, ostrosłup czworokątny.
Walec: Ma dwie podstawy, które są kołami, i powierzchnię boczną, która jest prostokątem zwiniętym w rurę.
Stożek: Ma jedną podstawę, która jest kołem, i powierzchnię boczną, która zwęża się do jednego punktu (wierzchołka stożka).
Kula: To figura, w której wszystkie punkty leżą w tej samej odległości od jednego punktu (środka kuli).

Objętość

Objętość: To ilość miejsca, jaką zajmuje figura w przestrzeni. Objętość liczymy, używając wzorów. Objętość podajemy w jednostkach sześciennych, np. cm³, m³, km³.

Wzory na objętości:

Sześcian: Objętość = bok * bok * bok (a³)
Prostopadłościan: Objętość = bok * bok * wysokość (a * b * c)

Symetria

Oś symetrii: To prosta, która dzieli figurę na dwie identyczne części, tak że jedna część jest lustrzanym odbiciem drugiej. Niektóre figury mają jedną oś symetrii, niektóre więcej, a niektóre nie mają żadnej. Np. kwadrat ma 4 osie symetrii, prostokąt ma 2 osie symetrii, okrąg ma nieskończenie wiele osi symetrii.

Środek symetrii: To punkt, względem którego figura jest symetryczna. Oznacza to, że jeśli poprowadzimy prostą przez ten punkt, to po obu stronach punktu będą znajdowały się punkty figury w tej samej odległości od środka symetrii. Np. kwadrat ma środek symetrii, okrąg ma środek symetrii, prostokąt ma środek symetrii.

Co jeszcze warto wiedzieć?

Uważnie czytaj treść zadania. Zrozum, o co pytają.
Rysuj rysunki pomocnicze. To często bardzo ułatwia rozwiązanie zadania.
Pamiętaj o jednostkach.
Sprawdzaj swoje obliczenia.
Nie panikuj! Nawet jeśli nie wiesz, jak rozwiązać zadanie od razu, spróbuj pomyśleć krok po kroku.

Mam nadzieję, że te wyjaśnienia pomogą wam na sprawdzianie. Powodzenia! Pamiętajcie, że najważniejsze to zrozumieć, o co chodzi, a nie tylko zapamiętać wzory. Wtedy matematyka stanie się łatwiejsza i przyjemniejsza! Jeżeli macie jeszcze jakieś pytania, pytajcie śmiało!