Sprawdzian Z Graniastosłupów Klasa 2 Gimnazjum

Hej uczniowie! Czeka Was sprawdzian z graniastosłupów w drugiej klasie gimnazjum? Bez obaw! Rozłóżmy to zagadnienie na czynniki pierwsze, żeby wszystko było jasne i proste. Przygotujcie się na podróż po świecie brył!

Czym jest graniastosłup?

Wyobraźcie sobie pudełko po butach. Albo kawałek sera w kształcie trójkąta. To właśnie graniastosłupy! Graniastosłup to bryła, która ma dwie identyczne podstawy (wielokąty) połączone ścianami bocznymi (prostokątami lub równoległobokami). Najważniejsze, żeby podstawy były równoległe i identyczne.

Podstawa może być trójkątem, kwadratem, pięciokątem – dowolnym wielokątem! Od kształtu podstawy zależy nazwa graniastosłupa. Na przykład, jeśli podstawa to trójkąt, mamy graniastosłup trójkątny. A jeśli kwadrat – graniastosłup czworokątny, inaczej sześcian lub prostopadłościan.

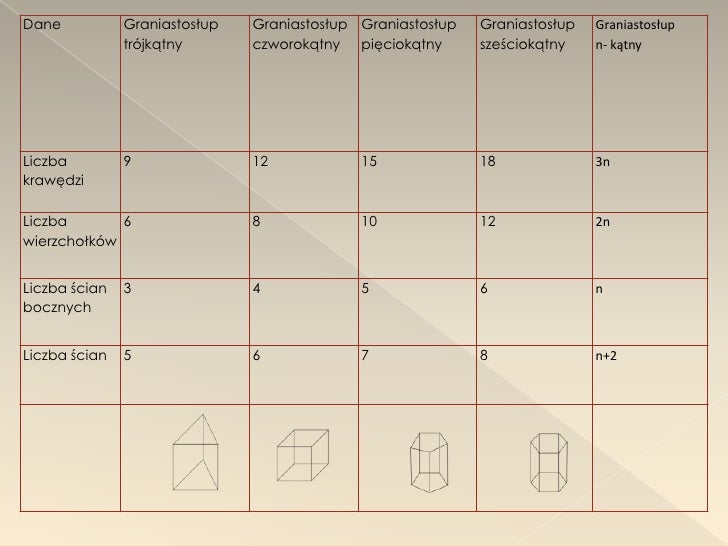
Elementy graniastosłupa

Graniastosłup ma kilka kluczowych elementów. Podstawy to te dwie identyczne figury na górze i na dole. Ściany boczne łączą podstawy. Krawędzie to linie, wzdłuż których stykają się ściany. Wierzchołki to punkty, w których zbiegają się krawędzie.

Pamiętajcie o tych nazwach! Będą potrzebne do rozwiązywania zadań na sprawdzianie. Wyobraźcie sobie graniastosłup jako budynek: podstawa to fundament i dach, ściany boczne to ściany budynku, krawędzie to krawędzie ścian, a wierzchołki to narożniki.

Rodzaje graniastosłupów

Graniastosłupy dzielimy na różne rodzaje. Najważniejszy podział to na graniastosłupy proste i graniastosłupy pochyłe. W graniastosłupie prostym ściany boczne są prostopadłe do podstawy (tworzą kąt prosty). W graniastosłupie pochyłym ściany boczne są nachylone do podstawy.

Dodatkowo, mamy graniastosłupy prawidłowe. Są to graniastosłupy proste, których podstawy są wielokątami foremnymi (czyli mają wszystkie boki i kąty równe). Na przykład, graniastosłup prawidłowy trójkątny ma w podstawie trójkąt równoboczny.

Pole powierzchni i objętość

Na sprawdzianie mogą pojawić się zadania dotyczące pola powierzchni i objętości graniastosłupa. Pole powierzchni to suma pól wszystkich ścian. Objętość to ilość miejsca, jaką zajmuje graniastosłup.

Do obliczenia pola powierzchni potrzebujemy wzoru: P = 2 * Pp + Pb, gdzie Pp to pole podstawy, a Pb to pole powierzchni bocznej. Do obliczenia objętości używamy wzoru: V = Pp * H, gdzie Pp to pole podstawy, a H to wysokość graniastosłupa.

Pamiętajcie o jednostkach! Pole powierzchni podajemy w jednostkach kwadratowych (np. cm², m²), a objętość w jednostkach sześciennych (np. cm³, m³).

Powodzenia na sprawdzianie! Teraz, gdy znacie podstawy, ćwiczcie rozwiązywanie zadań i na pewno dacie radę!