Sprawdzian Z Graniastosłupów I Ostrosłupów

Witaj! Zbliża się sprawdzian z graniastosłupów i ostrosłupów? Rozumiem. To może być stresujące. Wiele osób zmaga się z geometrią przestrzenną, a te figury potrafią sprawić trudności nawet tym, którzy lubią matematykę. Pamiętaj, że nie jesteś sam w tym! Ten artykuł ma za zadanie pomóc Ci zrozumieć kluczowe zagadnienia, uprościć skomplikowane koncepcje i dać Ci pewność siebie przed nadchodzącym sprawdzianem.

Zamiast skupiać się tylko na wzorach, postaramy się zrozumieć, gdzie te figury spotykamy w życiu codziennym i dlaczego właściwie warto się nimi zajmować.

Dlaczego graniastosłupy i ostrosłupy są ważne?

Możesz się zastanawiać: "Po co mi to wszystko?". Odpowiedź jest prosta: geometria przestrzenna otacza nas wszędzie! Pomyśl o budynkach, pudełkach, piramidach w Egipcie, czy nawet o kształcie dachu Twojego domu. Zrozumienie zasad rządzących tymi bryłami pozwala lepiej rozumieć świat wokół nas, a także rozwija umiejętność logicznego myślenia i rozwiązywania problemów. To umiejętności przydatne nie tylko na matematyce, ale i w wielu innych dziedzinach życia.

Spójrzmy na kilka przykładów:

Architektura: Projektowanie budynków, mostów, i innych konstrukcji wymaga precyzyjnego operowania geometrią przestrzenną.
Inżynieria: Obliczanie wytrzymałości materiałów, projektowanie maszyn, wszystko to opiera się na znajomości geometrii brył.
Grafika komputerowa: Tworzenie trójwymiarowych modeli w grach i animacjach również wymaga zrozumienia zasad geometrii przestrzennej.
Opakowania: Projektowanie optymalnych kształtów opakowań, aby zmaksymalizować wykorzystanie przestrzeni i zminimalizować koszty transportu.

Czym różni się graniastosłup od ostrosłupa?

To fundamentalne pytanie! Spróbujmy to uprościć:

Graniastosłup

Wyobraź sobie pudełko. Ma dwie identyczne podstawy (górną i dolną), które są wielokątami (np. trójkąty, kwadraty, pięciokąty). Ściany boczne graniastosłupa to prostokąty (lub równoległoboki). Najprostszy przykład to zwykły prostopadłościan.

Ma dwie podstawy.
Ściany boczne są prostokątami lub równoległobokami.
Przykłady: prostopadłościan, sześcian, graniastosłup trójkątny.

Możemy wyróżnić graniastosłupy proste (ściany boczne są prostopadłe do podstawy) i graniastosłupy pochyłe (ściany boczne nie są prostopadłe do podstawy).

Ostrosłup

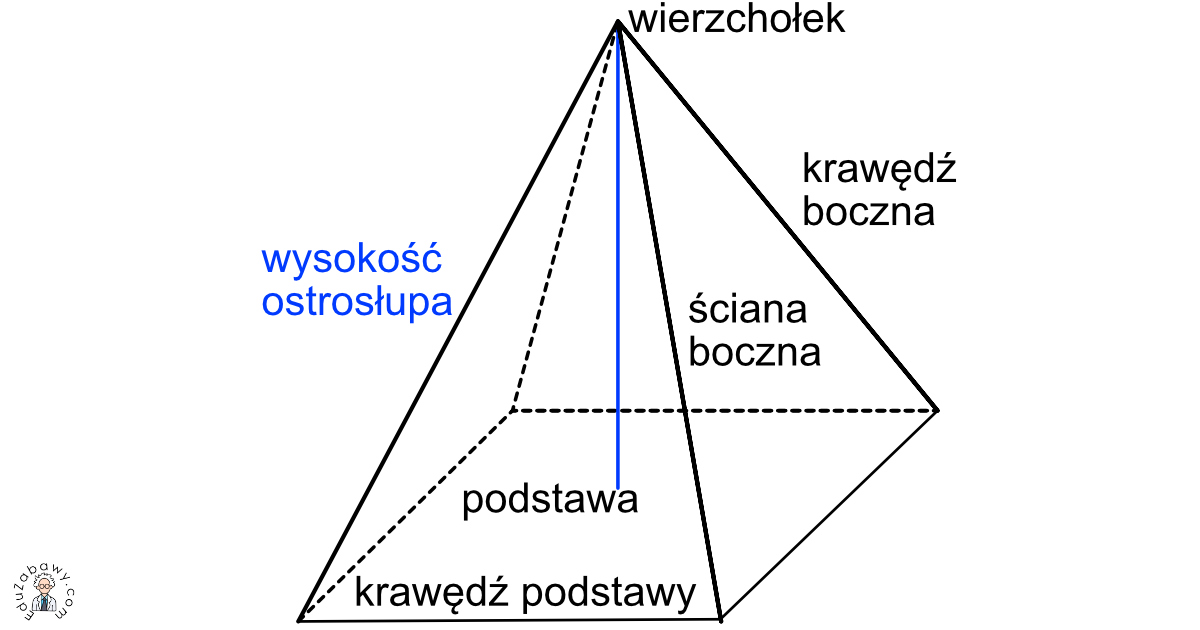
Wyobraź sobie piramidę. Ma jedną podstawę (wielokąt) i ściany boczne, które są trójkątami zbiegającymi się w jednym punkcie – wierzchołku ostrosłupa.

Ma jedną podstawę.
Ściany boczne są trójkątami.
Wszystkie ściany boczne zbiegają się w jednym punkcie - wierzchołku.
Przykłady: ostrosłup trójkątny (czworościan), ostrosłup kwadratowy, ostrosłup sześciokątny.

Podobnie jak graniastosłupy, ostrosłupy też mogą być proste (wysokość pada na środek podstawy) i pochyłe (wysokość nie pada na środek podstawy).

Kluczowe wzory, które musisz znać

Wzory to ważny element, ale pamiętaj, że ważniejsze jest zrozumienie, skąd się biorą. Niemniej jednak, na sprawdzianie warto mieć je w głowie. Oto najważniejsze:

Graniastosłupy

Pole powierzchni całkowitej (Pc): Pc = 2 * Pp + Pb, gdzie Pp to pole podstawy, a Pb to pole powierzchni bocznej.
Pole powierzchni bocznej (Pb): Pb = Obwód podstawy * Wysokość (dla graniastosłupów prostych).
Objętość (V): V = Pp * H, gdzie H to wysokość graniastosłupa.

Ostrosłupy

Pole powierzchni całkowitej (Pc): Pc = Pp + Pb, gdzie Pp to pole podstawy, a Pb to pole powierzchni bocznej.
Pole powierzchni bocznej (Pb): Trzeba obliczyć sumę pól wszystkich ścian bocznych (trójkątów).
Objętość (V): V = (1/3) * Pp * H, gdzie H to wysokość ostrosłupa.

Pamiętaj! Pole podstawy (Pp) zależy od tego, jaki wielokąt jest podstawą. Musisz znać wzory na pole trójkąta, kwadratu, prostokąta, rombu, trapezu, itp.

Najczęstsze błędy i jak ich unikać

Warto wiedzieć, gdzie najczęściej popełniane są błędy, aby ich unikać:

Pomylenie wzorów: Upewnij się, że używasz właściwego wzoru dla danej figury. Napisz sobie ściągawkę z najważniejszymi wzorami.
Błędy w obliczeniach: Sprawdzaj obliczenia, szczególnie przy mnożeniu i dzieleniu ułamków. Używaj kalkulatora, jeśli masz taką możliwość.
Zapominanie o jednostkach: Pamiętaj o podawaniu jednostek (cm² dla pola, cm³ dla objętości).
Nierozumienie zadania: Przeczytaj uważnie treść zadania i upewnij się, że wiesz, co masz obliczyć. Spróbuj narysować rysunek pomocniczy.
Brak rysunku pomocniczego: Rysunek często ułatwia zrozumienie zadania i znalezienie rozwiązania.

Jak efektywnie się uczyć?

Samo czytanie podręcznika nie wystarczy. Trzeba aktywnie ćwiczyć i angażować się w proces uczenia się.

Rozwiązuj zadania: Im więcej zadań rozwiążesz, tym lepiej zrozumiesz materiał. Zacznij od prostych zadań, a następnie przejdź do bardziej skomplikowanych.
Ucz się z kimś: Uczenie się w grupie może być bardzo efektywne. Możecie się nawzajem tłumaczyć materiał, rozwiązywać zadania i odpowiadać na pytania.
Wykorzystaj zasoby online: W Internecie znajdziesz wiele materiałów edukacyjnych, takich jak filmy instruktażowe, interaktywne zadania i quizy.
Zadawaj pytania: Nie bój się zadawać pytań nauczycielowi lub innym osobom, które dobrze rozumieją materiał. Lepiej zapytać i rozwiać wątpliwości, niż iść na sprawdzian z lukami w wiedzy.
Rób regularne przerwy: Uczenie się bez przerw może być męczące i mało efektywne. Rób sobie krótkie przerwy co 30-45 minut.
Wykorzystaj wizualizacje: Używaj modeli 3D, programów do rysowania, a nawet buduj modele z papieru, aby lepiej zrozumieć kształty i relacje przestrzenne.

Counterpoint: Czy to naprawdę takie ważne?

Niektórzy mogą argumentować, że geometria przestrzenna nie jest im potrzebna w życiu. Może i nie będą projektować budynków, ale umiejętność logicznego myślenia, rozwiązywania problemów i wizualizacji przestrzennej jest cenna w wielu dziedzinach, od planowania budżetu po organizowanie przestrzeni w domu. Ponadto, matematyka, w tym geometria, uczy nas dyscypliny i systematyczności, a to cechy przydatne w każdej dziedzinie życia.

Przykładowe zadanie i jego rozwiązanie

Zadanie: Oblicz objętość ostrosłupa prawidłowego czworokątnego, w którym krawędź podstawy ma długość 6 cm, a wysokość ostrosłupa wynosi 8 cm.

Rozwiązanie:

Oblicz pole podstawy (Pp): Podstawą jest kwadrat, więc Pp = a² = 6² = 36 cm².
Oblicz objętość (V): V = (1/3) * Pp * H = (1/3) * 36 * 8 = 96 cm³.

Odpowiedź: Objętość ostrosłupa wynosi 96 cm³.

Pamiętaj o odpoczynku przed sprawdzianem!

Dzień przed sprawdzianem nie siedź do późna i nie wkuwaj na siłę. Odpocznij, zjedz coś dobrego i postaraj się zrelaksować. Wyspany umysł pracuje o wiele lepiej!

Podsumowanie i dalsze kroki

Mam nadzieję, że ten artykuł pomógł Ci uporządkować wiedzę i przygotować się do sprawdzianu z graniastosłupów i ostrosłupów. Pamiętaj, że kluczem do sukcesu jest regularna nauka, rozwiązywanie zadań i zadawanie pytań. Geometria przestrzenna może wydawać się trudna, ale z odpowiednim podejściem i dużą dozą cierpliwości na pewno ją opanujesz. Nie bój się wyzwań! Każdy krok naprzód, nawet ten najmniejszy, to postęp w drodze do celu.

Czy po przeczytaniu tego artykułu czujesz się pewniej przed sprawdzianem? Jakie zagadnienie sprawia Ci jeszcze trudność i wymaga dodatkowej uwagi?