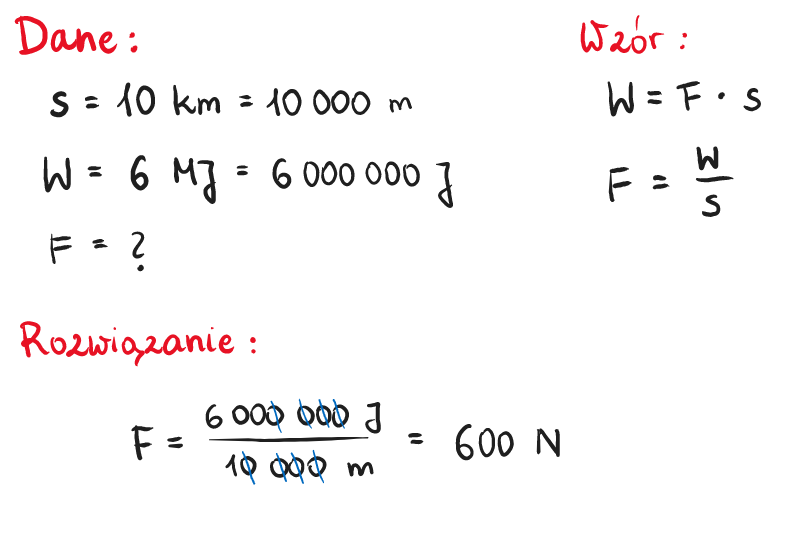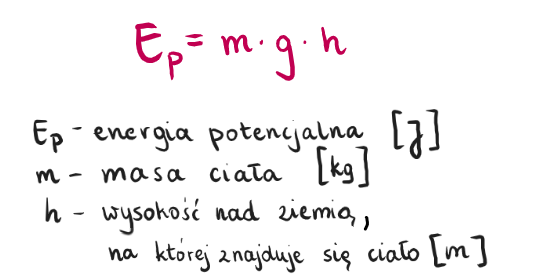Sprawdzian Z Fizyki Praca Moc Energia

Pamiętacie sprawdzian z fizyki? Ten moment grozy, kiedy kartka lądowała na ławce, a wasz mózg postanawiał nagle przejść na emeryturę?

Praca – ten wysiłek się opłaca… czy aby na pewno?

Mówią, że praca uszlachetnia. Pewnie tak. Ale czy naprawdę muszę obliczać pracę, jaką wykonuje Jaś, ciągnąc sanki pod górę? Serio? Jaś mógłby po prostu wziąć narty! Albo poprosić kolegę. Albo... zaczekać na odwilż. Prościej i mniej liczenia. Nie sądzicie?

Wiem, wiem, to fizyka. Musimy wiedzieć, ile energii Jaś spalił. Ale nie oszukujmy się. Kto z nas liczy kalorie, idąc na spacer? No dobra, może niektórzy. Ale większość po prostu idzie!

Praca na sprawdzianie a praca w życiu

Co więcej, ta praca z fizyki jakoś dziwnie różni się od tej "prawdziwej". Na sprawdzianie wszystko jest idealne. Żadnych strat energii. Żadnego tarcia (no, chyba że ktoś to specjalnie uwzględni). W życiu? Schody zaczynają się już przy próbie otwarcia słoika z ogórkami.

Moc – czyli kto szybciej zje pączka?

Kolejny hit: moc. Czyli jak szybko coś robimy. I od razu nasuwa się pytanie: po co się spieszyć? Szczególnie, jeśli chodzi o jedzenie pączków. Czy ważniejsze jest, kto zje pączka w 5 sekund, czy kto delektuje się nim przez 5 minut? Moim zdaniem zdecydowanie ta druga opcja. Smak > moc.

No dobra, rozumiem, że chodzi o wzory i obliczenia. Ale czy naprawdę potrzebujemy znać moc silnika kosiarki, żeby skosić trawnik? Wystarczy, że kosiarka działa, a trawa jest krótka. Amen.

Energia – czyli dlaczego nie mogę spać?

I na koniec – energia. To chyba najbardziej abstrakcyjne pojęcie. Energia kinetyczna, potencjalna, wewnętrzna... Czasami mam wrażenie, że mam tylko jedną: energię do narzekania na fizykę.

Pamiętam te zadania: "Oblicz energię kinetyczną lecącego jabłka". Serio? Czy naprawdę ktoś mierzył prędkość spadającego jabłka? Einstein miał ważniejsze rzeczy na głowie! A ja wolę zjeść to jabłko, niż liczyć jego energię.

"Sprawdzian z fizyki to jak gra. Tylko zasady są dziwne i nikt nie tłumaczy, jak wygrać."

Niby to wszystko ma praktyczne zastosowanie. Budowa mostów, elektrownie, rakiety kosmiczne. Fajnie. Ale czy naprawdę muszę wiedzieć, jak działa elektrownia jądrowa, żeby włączyć światło? Nie sądzę.

Podsumowując: sprawdzian z fizyki to wyzwanie. Ale życie jest jeszcze większym. I czasem lepiej po prostu cieszyć się chwilą, zamiast wszystko obliczać. A jeśli Jaś chce ciągnąć sanki pod górę, to niech ciągnie. I niech nikt mu nie przeszkadza! Tylko żeby potem zjadł porządny obiad, bo energia mu się przyda!