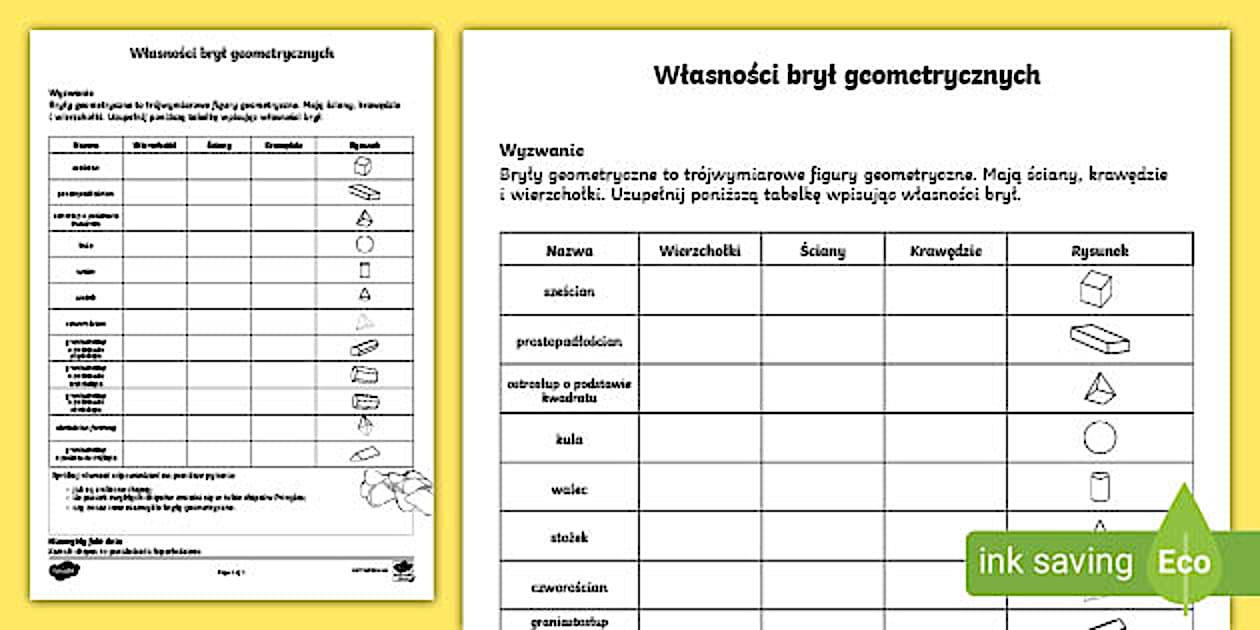
Sprawdzian Z Figur Cwiczenia Z Pomyslem Klasa 3

Edukacja matematyczna na etapie klasy 3 szkoły podstawowej stanowi fundament dla dalszego rozwoju umiejętności logicznego myślenia i rozwiązywania problemów. Właśnie w tym okresie dzieci poznają podstawowe figury geometryczne i uczą się je rozpoznawać. Sprawdzian z figur w klasie 3 nie musi być stresującym wydarzeniem. Można go potraktować jako kreatywne wyzwanie, które wzmocni wiedzę i zachęci do dalszej nauki.
Dlaczego Figury Geometryczne Są Ważne w Klasie 3?
Figury geometryczne, takie jak kwadrat, prostokąt, trójkąt i koło, są wszędzie wokół nas. Ucząc się je rozpoznawać i opisywać, dzieci rozwijają:
- Myślenie przestrzenne: Zdolność do wyobrażania sobie i manipulowania obiektami w przestrzeni.
- Umiejętności obserwacji: Zwracanie uwagi na detale i różnice w kształtach.
- Logiczne rozumowanie: Porównywanie i klasyfikowanie figur według ich właściwości.
- Słownictwo matematyczne: Posługiwanie się poprawnymi terminami związanymi z geometrią.
Dlatego sprawdzian z figur jest ważnym elementem oceny postępów ucznia w tym zakresie.
Pomysłowe Ćwiczenia na Sprawdzian z Figur
Tradycyjne sprawdziany często opierają się na suchym wkuwaniu definicji. Można jednak podejść do tego tematu kreatywnie, angażując uczniów w bardziej aktywne i interaktywne formy nauki. Oto kilka pomysłów:
1. Układanki z Figur
Przygotuj zestaw figur geometrycznych wyciętych z kolorowego papieru lub pianki. Poproś uczniów o układanie z nich różnych obrazków, np. domku, drzewa, robota. Następnie dzieci mogą opisywać, z jakich figur składa się ich praca, np. "Dom ma kwadratową podstawę i trójkątny dach". To ćwiczenie rozwija kreatywność i utrwala nazwy figur.
2. Polowanie na Figury w Otoczeniu
Wykorzystaj klasę lub otoczenie szkolne jako przestrzeń do poszukiwań. Poproś uczniów o znalezienie przedmiotów, które przypominają określone figury geometryczne. Na przykład: "Znajdź coś w kształcie koła" (zegar, talerz) lub "Znajdź coś w kształcie prostokąta" (książka, tablica). To ćwiczenie uczy zastosowania wiedzy w praktyce.
3. Rysowanie z Instrukcjami
Podaj instrukcje, które opisują, jakie figury i w jakiej kolejności należy narysować. Na przykład: "Narysuj duży kwadrat. W środku kwadratu narysuj małe koło. Na górze kwadratu dorysuj trójkąt". To ćwiczenie rozwija umiejętność czytania ze zrozumieniem i precyzję w rysowaniu.
4. Klasyfikacja Figur
Przygotuj zestaw figur o różnych kolorach, rozmiarach i kształtach. Poproś uczniów o pogrupowanie ich według określonych kryteriów, np. "Pogrupuj figury według kształtu" lub "Pogrupuj figury według koloru". To ćwiczenie rozwija umiejętność analizy i klasyfikacji.
5. Quiz z Zagadkami
Przygotuj quiz z zagadkami dotyczącymi figur geometrycznych. Na przykład: "Mam cztery boki równej długości i cztery kąty proste. Co to jestem?" (Kwadrat) lub "Mam trzy boki i trzy kąty. Co to jestem?" (Trójkąt). To ćwiczenie uczy skojarzeń i logicznego myślenia.
Real-World Examples and Data
Badania pokazują, że dzieci, które uczą się geometrii poprzez zabawę i interakcję, osiągają lepsze wyniki na późniejszych etapach edukacji. Na przykład, w krajach, gdzie kładzie się duży nacisk na edukację matematyczną opartą na praktycznych przykładach (np. Singapur), uczniowie osiągają jedne z najwyższych wyników w testach międzynarodowych.
Przykład: W jednym z badań przeprowadzonych w szkole podstawowej, dwie grupy uczniów uczyły się o figurach geometrycznych. Jedna grupa korzystała z tradycyjnych podręczników i ćwiczeń, a druga grupa uczestniczyła w zajęciach opartych na zabawach i grach. Po tygodniu obie grupy przeszły sprawdzian. Uczniowie z grupy, która uczyła się poprzez zabawę, uzyskali średnio o 15% wyższe wyniki.
Podsumowanie i Zachęta do Działania
Sprawdzian z figur w klasie 3 nie musi być powodem do stresu. Można go potraktować jako okazję do kreatywnego powtórzenia materiału i utrwalenia wiedzy. Wykorzystując pomysłowe ćwiczenia, gry i zabawy, można sprawić, że nauka geometrii stanie się dla dzieci przyjemna i efektywna. Pamiętajmy, że kluczem jest zaangażowanie i dostosowanie metod nauczania do indywidualnych potrzeb ucznia.
Zachęcamy nauczycieli i rodziców do eksperymentowania z różnymi formami nauki i do poszukiwania kreatywnych sposobów na zainteresowanie dzieci matematyką. Im więcej pozytywnych doświadczeń związanych z nauką, tym większa szansa na to, że dzieci polubią ten przedmiot i osiągną sukcesy w przyszłości.