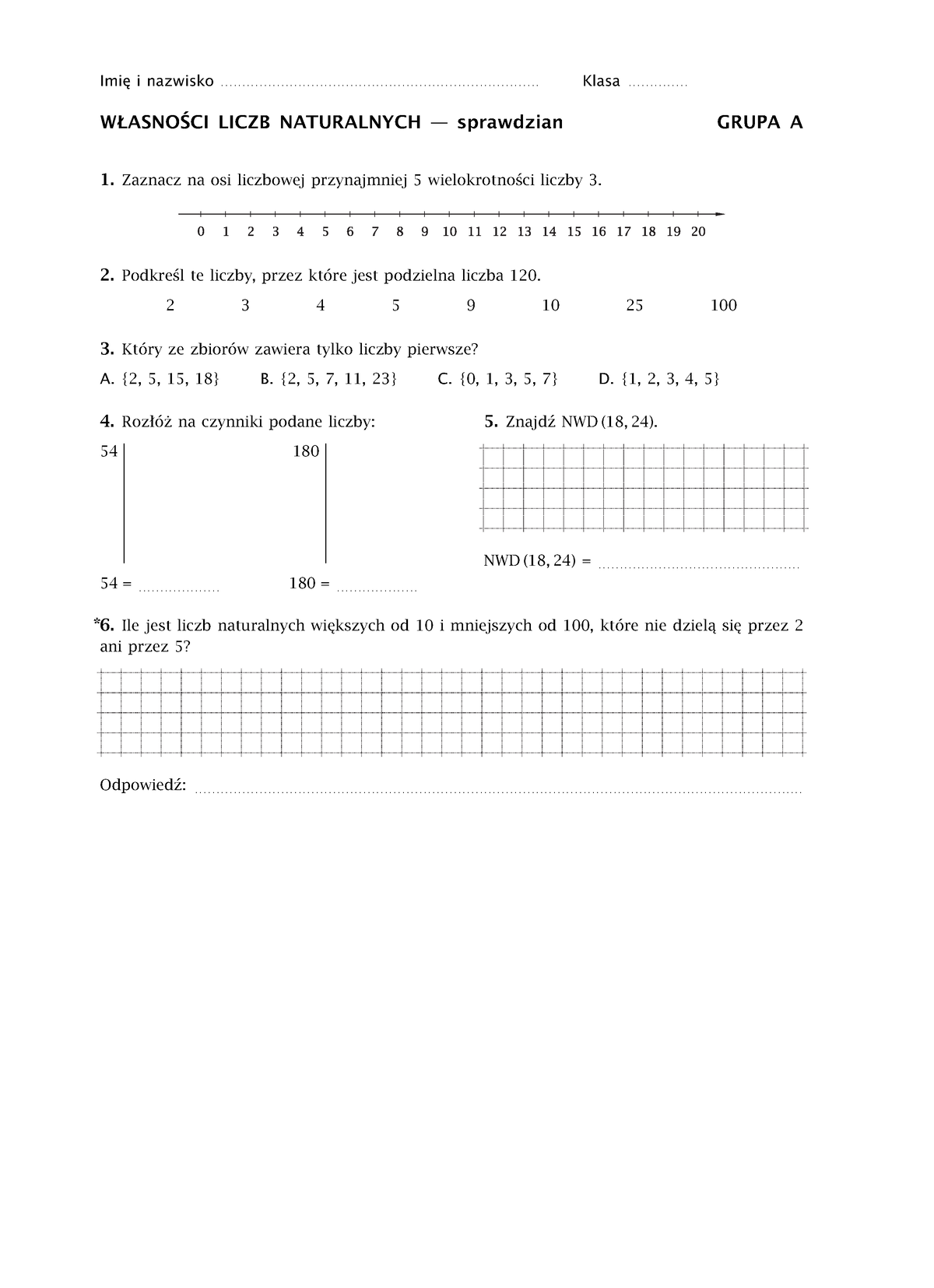
Sprawdzian Z Działu Własności Liczb Naturalnych Klasa 5

Hej Dzieciaki! Widzę, że zbliża się sprawdzian z własności liczb naturalnych w klasie 5 i macie kilka pytań. Spokojnie, postaram się wszystko wytłumaczyć najprościej jak się da. Gotowi? Zaczynamy!

Najpierw zajmijmy się dzielnikami i wielokrotnościami. Wyobraźcie sobie, że macie paczkę cukierków. Dzielnik to liczba, przez którą możecie podzielić te cukierki tak, żeby nikomu nie brakowało żadnego kawałka. Czyli, jeśli macie 12 cukierków, to możecie je podzielić na 1 osobę (każda dostanie 12), na 2 osoby (każda dostanie 6), na 3 osoby (każda dostanie 4), na 4 osoby (każda dostanie 3), na 6 osób (każda dostanie 2) i na 12 osób (każda dostanie 1). Zatem dzielniki liczby 12 to: 1, 2, 3, 4, 6 i 12.

Wielokrotność to z kolei liczba, która powstaje, gdy mnożymy naszą liczbę przez kolejne liczby naturalne. Czyli wielokrotności liczby 3 to: 3 (3x1), 6 (3x2), 9 (3x3), 12 (3x4), 15 (3x5) i tak dalej, aż do nieskończoności.

Żeby sprawdzić, czy dana liczba jest dzielnikiem innej liczby, po prostu dzielicie. Jeśli wynik jest liczbą całkowitą (bez ułamków), to znaczy, że ta liczba jest dzielnikiem.

Rozkład Liczby na Czynniki Pierwsze

Teraz przejdźmy do rozkładu liczby na czynniki pierwsze. Co to takiego? To rozbicie liczby na mniejsze kawałki, ale takie, których już nie da się podzielić na mniejsze, poza jedynką i samą sobą. Takie liczby nazywamy liczbami pierwszymi. Przykładami liczb pierwszych są: 2, 3, 5, 7, 11, 13, 17, 19 i tak dalej.

Weźmy na przykład liczbę 30. Jak ją rozłożyć na czynniki pierwsze?

1. Myślimy, przez jaką najmniejszą liczbę pierwszą dzieli się 30? Przez 2! 30 : 2 = 15
2. Teraz, przez jaką liczbę pierwszą dzieli się 15? Przez 3! 15 : 3 = 5
3. 5 dzieli się tylko przez 5. 5 : 5 = 1

Zatem rozkład liczby 30 na czynniki pierwsze to: 2 x 3 x 5.

Sprawdzamy, czy się zgadza: 2 x 3 x 5 = 30. Bingo!

Inny przykład: liczba 48.

1. 48 : 2 = 24
2. 24 : 2 = 12
3. 12 : 2 = 6
4. 6 : 2 = 3
5. 3 : 3 = 1

Rozkład liczby 48 na czynniki pierwsze to: 2 x 2 x 2 x 2 x 3. Możemy to zapisać krócej jako: 2⁴ x 3.

Cechy podzielności liczb

Żeby sprawdzić, czy liczba dzieli się przez inną, bez wykonywania dzielenia, możemy użyć cech podzielności. One bardzo ułatwiają życie!

• Podzielność przez 2: Liczba dzieli się przez 2, jeśli jej ostatnia cyfra to 0, 2, 4, 6 lub 8. Czyli liczba jest parzysta.
• Podzielność przez 3: Liczba dzieli się przez 3, jeśli suma jej cyfr dzieli się przez 3. Na przykład, liczba 123: 1 + 2 + 3 = 6. 6 dzieli się przez 3, więc 123 też dzieli się przez 3.
• Podzielność przez 4: Liczba dzieli się przez 4, jeśli liczba utworzona przez jej dwie ostatnie cyfry dzieli się przez 4. Na przykład, liczba 216: 16 dzieli się przez 4, więc 216 też dzieli się przez 4.
• Podzielność przez 5: Liczba dzieli się przez 5, jeśli jej ostatnia cyfra to 0 lub 5.
• Podzielność przez 9: Liczba dzieli się przez 9, jeśli suma jej cyfr dzieli się przez 9. Na przykład, liczba 819: 8 + 1 + 9 = 18. 18 dzieli się przez 9, więc 819 też dzieli się przez 9.
• Podzielność przez 10: Liczba dzieli się przez 10, jeśli jej ostatnia cyfra to 0.

Pamiętajcie, że cechy podzielności to tylko skróty. Jeśli nie jesteście pewni, zawsze możecie wykonać dzielenie.

Liczby pierwsze i liczby złożone

Już wspomnieliśmy o liczbach pierwszych. Przypomnijmy: liczba pierwsza to taka, która ma tylko dwa dzielniki: 1 i samą siebie. Przykłady: 2, 3, 5, 7, 11, 13.

Liczba złożona to taka, która ma więcej niż dwa dzielniki. Czyli można ją podzielić przez coś więcej niż tylko 1 i samą siebie. Przykłady: 4, 6, 8, 9, 10, 12.

Liczba 1 nie jest ani liczbą pierwszą, ani liczbą złożoną. To taki wyjątek.

NWD i NWW

NWD to Największy Wspólny Dzielnik. Czyli największa liczba, przez którą dzielą się dwie (lub więcej) liczby. NWW to Najmniejsza Wspólna Wielokrotność. Czyli najmniejsza liczba, która jest wielokrotnością dwóch (lub więcej) liczb.

Jak znaleźć NWD i NWW?

Przykład: Znajdź NWD i NWW liczb 12 i 18.

1. Rozkładamy liczby na czynniki pierwsze:

   • 12 = 2 x 2 x 3 = 2² x 3
   • 18 = 2 x 3 x 3 = 2 x 3²

2. NWD: Bierzemy tylko wspólne czynniki w najniższej potędze.

   • Wspólne czynniki to 2 i 3.
   • Najniższa potęga 2 to 2¹ (czyli po prostu 2).
   • Najniższa potęga 3 to 3¹ (czyli po prostu 3).
   • NWD(12, 18) = 2 x 3 = 6

3. NWW: Bierzemy wszystkie czynniki (wspólne i niewspólne) w najwyższej potędze.

   • Czynniki to 2 i 3.
   • Najwyższa potęga 2 to 2² (czyli 4).
   • Najwyższa potęga 3 to 3² (czyli 9).
   • NWW(12, 18) = 2² x 3² = 4 x 9 = 36

Praktyczne zastosowanie

To wszystko nie jest tylko dla sprawdzianu! Dzielniki, wielokrotności, NWD i NWW przydają się w życiu codziennym, na przykład:

• Dzielenie się słodyczami: Chcesz podzielić równo paczkę cukierków między kolegów. Potrzebujesz dzielników.
• Planowanie podróży: Autobusy linii A kursują co 15 minut, a autobusy linii B co 20 minut. Kiedy znowu pojadą razem z tego samego przystanku? Potrzebujesz NWW.
• Układanie kafelków: Masz kafelki o wymiarach 12 cm i 18 cm. Jaką najmniejszą kwadratową powierzchnię możesz nimi wyłożyć, żeby nie trzeba było żadnego docinać? Potrzebujesz NWW.

Kilka dodatkowych wskazówek na sprawdzian:

• Czytaj uważnie polecenia: Zwróć uwagę, o co dokładnie pytają.
• Pisz czytelnie: Żeby nauczyciel mógł bez problemu odczytać Twoje odpowiedzi.
• Sprawdzaj swoje obliczenia: Zawsze warto upewnić się, że nie popełniłeś żadnego błędu.
• Nie stresuj się: Pamiętaj, że sprawdzian to tylko okazja do sprawdzenia swojej wiedzy.

Pamiętajcie, że ćwiczenie czyni mistrza! Im więcej zadań rozwiążecie, tym lepiej zrozumiecie te wszystkie zagadnienia. Powodzenia na sprawdzianie!