Sprawdzian Ułamki Zwykłe Klasa 5

Rozumiem. Sprawdzian z ułamków zwykłych w klasie piątej... To może być stresujące! Sam pamiętam, jak w piątej klasie niektóre tematy wydawały się naprawdę trudne. Ale spokojnie, ułamki zwykłe wcale nie są takie straszne, jak się wydają. Pomyśl o nich jak o kawałkach pizzy! Zaraz pokażę, jak sobie z nimi poradzić.

Dlaczego ułamki zwykłe są ważne? Może się wydawać, że to tylko abstrakcyjne liczby, które trzeba zrozumieć na sprawdzian. Ale ułamki są wszędzie!

Gotowanie: Przepisy często wymagają użycia ułamków - np. pół szklanki mąki (1/2) albo ćwierć łyżeczki soli (1/4).
Podział: Kiedy dzielisz się czymś z przyjaciółmi - np. pizzą, ciastem, albo nawet obowiązkami domowymi - używasz ułamków.
Pomiar: Odmierzasz długość kawałka sznurka, szerokość kartki, a nawet czas – to wszystko ułamki!
Finanse: Rabat 25% to ułamek, który wpływa na to, ile zapłacisz.

Zrozumienie ułamków zwykłych to klucz do wielu codziennych sytuacji. To nie tylko teoria, ale praktyczna umiejętność, która przyda Ci się przez całe życie.

Czym są ułamki zwykłe?

Ułamek zwykły to nic innego jak część całości. Składa się z dwóch liczb oddzielonych kreską:

Licznik (góra): Mówi, ile części bierzemy.
Mianownik (dół): Mówi, na ile części podzielona jest całość.

Na przykład, ułamek 1/4 (czytamy: jedna czwarta) oznacza, że całość została podzielona na 4 równe części i bierzemy jedną z nich. Wyobraź sobie pizzę pokrojoną na 4 kawałki – 1/4 to jeden kawałek tej pizzy.

Rodzaje ułamków:

Ułamki właściwe: Licznik jest mniejszy niż mianownik (np. 2/5). Oznaczają one mniej niż całą jedność.
Ułamki niewłaściwe: Licznik jest większy lub równy mianownikowi (np. 5/2, 3/3). Oznaczają one całą jedność lub więcej niż całą jedność.
Liczby mieszane: Składają się z liczby całkowitej i ułamka właściwego (np. 1 1/2). Reprezentują to samo co ułamki niewłaściwe, ale w innej formie.

Działania na ułamkach – Krok po kroku

Teraz przejdźmy do konkretnych działań, które mogą pojawić się na sprawdzianie.

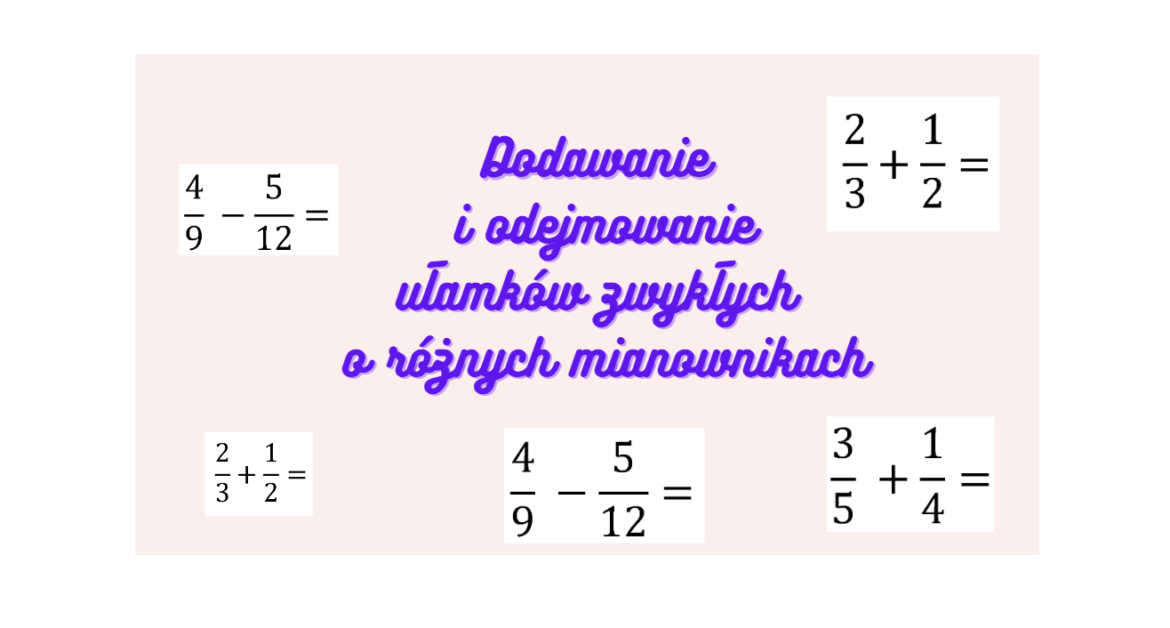
Sprowadzanie ułamków do wspólnego mianownika

To podstawa do porównywania i dodawania/odejmowania ułamków. Ułamki możemy porównywać i dodawać/odejmować tylko wtedy, gdy mają taki sam mianownik.

Jak to zrobić?

Znajdź wspólny mianownik: Najczęściej jest to najmniejsza wspólna wielokrotność (NWW) mianowników. Możesz ją znaleźć, wypisując wielokrotności każdego mianownika, aż znajdziesz taką samą liczbę.
Rozszerz ułamki: Pomnóż licznik i mianownik każdego ułamka przez taką liczbę, aby w mianowniku otrzymać wspólny mianownik.

Przykład: Sprowadź ułamki 1/3 i 1/4 do wspólnego mianownika.

NWW (3, 4) = 12

1/3 = (1 * 4) / (3 * 4) = 4/12

1/4 = (1 * 3) / (4 * 3) = 3/12

Dodawanie i odejmowanie ułamków

Kiedy ułamki mają już wspólny mianownik, dodawanie i odejmowanie staje się proste:

Dodaj lub odejmij liczniki: Mianownik pozostaje bez zmian.

Przykład: 4/12 + 3/12 = (4 + 3) / 12 = 7/12

Przykład: 5/8 - 1/8 = (5 - 1) / 8 = 4/8

Dodawanie i odejmowanie liczb mieszanych: Można robić na dwa sposoby:

Sposób 1: Zamień liczby mieszane na ułamki niewłaściwe, a następnie dodaj/odejmij.
Sposób 2: Dodaj/odejmij osobno części całkowite i ułamkowe (pamiętaj o sprowadzeniu ułamków do wspólnego mianownika). Jeśli część ułamkowa wyniku jest ułamkiem niewłaściwym, zamień ją na liczbę mieszaną i dodaj do części całkowitej.

Mnożenie ułamków

Mnożenie ułamków jest bardzo proste: Mnożymy licznik przez licznik, a mianownik przez mianownik.

Przykład: 2/3 * 1/2 = (2 * 1) / (3 * 2) = 2/6

Mnożenie ułamka przez liczbę całkowitą: Potraktuj liczbę całkowitą jako ułamek z mianownikiem 1 (np. 5 = 5/1), a następnie pomnóż jak zwykłe ułamki.

Mnożenie liczb mieszanych: Najpierw zamień liczby mieszane na ułamki niewłaściwe, a następnie pomnóż.

Dzielenie ułamków

Dzielenie ułamków to tak naprawdę mnożenie przez odwrotność drugiego ułamka.

Znajdź odwrotność drugiego ułamka: Zamień licznik z mianownikiem. Na przykład, odwrotnością ułamka 2/3 jest 3/2.
Pomnóż pierwszy ułamek przez odwrotność drugiego ułamka.

Przykład: 1/2 : 2/3 = 1/2 * 3/2 = 3/4

Dzielenie liczb mieszanych: Najpierw zamień liczby mieszane na ułamki niewłaściwe, a następnie dziel.

Upraszczanie ułamków

Upraszczanie (skracanie) ułamka polega na podzieleniu licznika i mianownika przez ten sam dzielnik różny od zera. Upraszczanie ułamka nie zmienia jego wartości, tylko zapisuje go w prostszej formie.

Jak to zrobić?

Znajdź największy wspólny dzielnik (NWD) licznika i mianownika.
Podziel licznik i mianownik przez NWD.

Przykład: Uprość ułamek 4/8.

NWD (4, 8) = 4

4/8 = (4 : 4) / (8 : 4) = 1/2

Typowe błędy i jak ich unikać

Oto kilka typowych błędów, które uczniowie popełniają podczas sprawdzianu z ułamków:

Zapominanie o sprowadzaniu do wspólnego mianownika przed dodawaniem/odejmowaniem.
Dodawanie/odejmowanie liczników i mianowników (np. 1/2 + 1/3 = 2/5 – BŁĄD!).
Brak upraszczania ułamków w wyniku.
Błędy w mnożeniu/dzieleniu, szczególnie przy liczbach mieszanych.
Pomylenie licznika z mianownikiem.

Pamiętaj o sprawdzeniu swoich obliczeń!

Przykładowe zadania i rozwiązania

Najlepszy sposób na opanowanie ułamków to ćwiczenia! Rozwiąż kilka przykładowych zadań:

Oblicz: 1/4 + 2/8 = ?
Oblicz: 3/5 - 1/10 = ?
Oblicz: 2/3 * 3/4 = ?
Oblicz: 1/2 : 1/4 = ?
Zamień 1 3/4 na ułamek niewłaściwy.
Zamień 7/3 na liczbę mieszaną.

Rozwiązania:

1/4 + 2/8 = 2/8 + 2/8 = 4/8 = 1/2
3/5 - 1/10 = 6/10 - 1/10 = 5/10 = 1/2
2/3 * 3/4 = 6/12 = 1/2
1/2 : 1/4 = 1/2 * 4/1 = 4/2 = 2
1 3/4 = (1 * 4 + 3) / 4 = 7/4
7/3 = 2 1/3

Co, jeśli i tak mam problem?

Nie martw się! Każdy uczy się w swoim tempie. Jeśli nadal masz trudności, spróbuj:

Poprosić o pomoc nauczyciela po lekcjach.
Poprosić o pomoc kolegę/koleżankę, który dobrze rozumie temat.
Poszukać dodatkowych materiałów online - jest mnóstwo stron i filmików z wyjaśnieniami.
Ćwiczyć, ćwiczyć, ćwiczyć! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz ułamki.
Pomyśl o ułamkach w kategoriach praktycznych, tak jak z pizzą, którą dzieli się z przyjaciółmi.

Pamiętaj, nauka to proces. Nie zrażaj się niepowodzeniami. Ważne, żeby próbować i się nie poddawać!

Sprawdzian z ułamków zwykłych w klasie piątej to ważny krok, ale nie koniec świata. Z odpowiednim przygotowaniem i nastawieniem dasz radę! Powodzenia!

Co zrobisz, żeby lepiej przygotować się do następnego sprawdzianu z ułamków? Czy znajdziesz dodatkowe zadania do rozwiązania, czy poprosisz kogoś o pomoc, czy skorzystasz z zasobów online? Wybierz swój sposób i zacznij działać już dziś!