Sprawdzian Twierdzenie Pitagorasa 1 Gimnazjum

Witajcie, przyszli mistrzowie Twierdzenia Pitagorasa! Przygotowujecie się do sprawdzianu? Świetnie! Razem przejdziemy przez najważniejsze zagadnienia. Pokażę Wam, jak krok po kroku rozwiązywać zadania. Zobaczycie, to wcale nie jest takie trudne!

Co to jest Twierdzenie Pitagorasa?

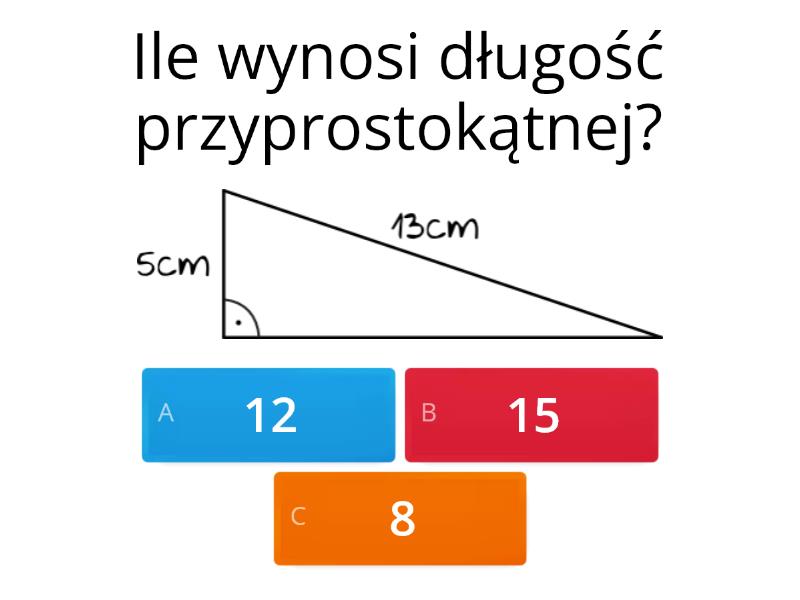
Twierdzenie Pitagorasa opisuje związek między bokami trójkąta prostokątnego. Zapamiętajcie, działa tylko dla trójkątów prostokątnych! Najdłuższy bok w takim trójkącie nazywamy przeciwprostokątną (c). Dwa krótsze boki to przyprostokątne (a i b).

Brzmienie twierdzenia: a² + b² = c². To znaczy, suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Wzór ten jest kluczem do sukcesu na sprawdzianie. Ćwiczcie jego zapamiętanie!

Jak stosować Twierdzenie Pitagorasa?

Mamy trójkąt prostokątny. Znamy długości dwóch boków i musimy obliczyć długość trzeciego. Wybieramy odpowiedni wzór. Podstawiamy dane do wzoru. Obliczamy!

Przykład: Przyprostokątne mają długości 3 cm i 4 cm. Oblicz długość przeciwprostokątnej. 3² + 4² = c². 9 + 16 = c². 25 = c². c = √25 = 5 cm. Zatem przeciwprostokątna ma długość 5 cm.

Zadania tekstowe

Często na sprawdzianie pojawiają się zadania tekstowe. Nie panikujcie! Najpierw przeczytajcie uważnie treść zadania. Zidentyfikujcie, co jest dane i czego szukacie. Narysujcie rysunek pomocniczy (trójkąt prostokątny!). Zastosujcie Twierdzenie Pitagorasa.

Przykład: Drabina o długości 5 metrów oparta jest o ścianę. Podstawa drabiny znajduje się 3 metry od ściany. Na jakiej wysokości sięga drabina na ścianie? Ściana i podłoga tworzą kąt prosty. Mamy trójkąt prostokątny. 3² + b² = 5². 9 + b² = 25. b² = 16. b = √16 = 4 metry. Drabina sięga na wysokość 4 metrów.

Podsumowanie

Pamiętajcie: Twierdzenie Pitagorasa dotyczy tylko trójkątów prostokątnych. Wzór: a² + b² = c², gdzie a i b to przyprostokątne, a c to przeciwprostokątna. Czytajcie uważnie zadania. Rysujcie rysunki pomocnicze. Ćwiczcie! Powodzenia na sprawdzianie!

Jesteście świetni i dacie radę! Trzymam kciuki!