Sprawdzian Symetrie Matematyka Z Plusem

Hej wszystkim! Zbliża się sprawdzian z symetrii i czujecie się lekko zagubieni? Bez obaw! Ten artykuł jest dla Was. Rozłożymy temat symetrii na czynniki pierwsze, tak żebyście podeszli do sprawdzianu z matematyki z plusem z pewnością siebie. Zaczynamy!

Czym w ogóle jest symetria?

Zacznijmy od podstaw. Symetria to nic innego jak harmonia, proporcjonalność i równowaga w wyglądzie jakiegoś obiektu. Mówiąc prościej, coś jest symetryczne, jeśli ma podobne lub identyczne części po obu stronach pewnej linii, punktu lub płaszczyzny.

Pomyślcie o ludzkiej twarzy. Idealnie (chociaż rzadko to się zdarza) powinna być symetryczna względem linii przechodzącej przez środek nosa. Lewa strona powinna być w miarę podobna do prawej. To jest właśnie symetria osiowa, ale o tym za chwilę.

Rodzaje symetrii - klucz do sukcesu na sprawdzianie!

Na sprawdzianie z matematyki z plusem prawdopodobnie spotkacie się z kilkoma rodzajami symetrii. Warto je dobrze znać i rozróżniać. Są to:

Symetria osiowa (zwierciadlana)

To chyba najpopularniejszy rodzaj symetrii. Wyobraźcie sobie, że macie kartkę papieru, rysujecie coś na niej, zginacie ją wzdłuż linii i odciskacie rysunek na drugą stronę. Linia zgięcia to oś symetrii. Obraz po jednej stronie osi jest lustrzanym odbiciem obrazu po drugiej stronie.

Definicja: Dwa punkty A i A' są symetryczne względem prostej (osi) *l*, jeśli prosta *l* jest prostopadła do odcinka AA' i przechodzi przez jego środek.

Przykłady z życia:

Motyl – jego skrzydła są symetryczne względem osi przechodzącej przez środek jego ciała.
Liść – wiele liści ma symetrię osiową.
Litera A, H, T, U, V, W, X, Y – jeśli narysujemy je starannie, zobaczymy, że mają oś symetrii (lub nawet kilka!).

Jak to rozpoznać na rysunku? Szukajcie linii, względem której rysunek wygląda jak odbicie w lustrze.

Symetria środkowa (punktowa)

Tutaj zamiast osi mamy środek symetrii, czyli punkt. Wyobraźcie sobie, że macie kartkę, rysujecie coś na niej, a następnie obracacie kartkę o 180 stopni wokół pewnego punktu. Jeśli po obrocie rysunek wygląda tak samo, to znaczy, że ma symetrię środkową względem tego punktu.

Definicja: Dwa punkty A i A' są symetryczne względem punktu S, jeśli punkt S jest środkiem odcinka AA'.

Przykłady z życia:

Znak drogowy "Ustąp pierwszeństwa" – ma symetrię środkową względem swojego środka.
Litera S, N, Z – jeśli obróćcie je o 180 stopni, wyglądają tak samo.
Okrąg – każdy punkt na środku okręgu jest jego środkiem symetrii.
Równoległobok – punkt przecięcia przekątnych jest jego środkiem symetrii.

Jak to rozpoznać na rysunku? Sprawdźcie, czy obracając rysunek o 180 stopni wokół danego punktu, otrzymacie ten sam rysunek.

Symetria obrotowa (wokół punktu)

To uogólnienie symetrii środkowej. Figura ma symetrię obrotową, jeśli istnieje punkt (środek obrotu), wokół którego można obrócić figurę o kąt mniejszy niż 360 stopni, tak aby figura pokryła się sama ze sobą.

Przykłady z życia:

Śnieżynka – ma symetrię obrotową. Można ją obrócić o 60 stopni (lub wielokrotność 60 stopni) wokół jej środka, a ona nadal będzie wyglądać tak samo.
Wiatrak – ma symetrię obrotową (zazwyczaj).
Kwiatek – wiele kwiatów ma symetrię obrotową.

Jak to rozpoznać na rysunku? Spróbujcie obracać rysunek wokół danego punktu i zobaczcie, czy po jakimś kącie obrotu rysunek wygląda tak samo.

Jak rozwiązywać zadania z symetrii na sprawdzianie?

Na sprawdzianie z matematyki z plusem możecie spodziewać się różnych typów zadań. Oto kilka wskazówek, jak je rozwiązywać:

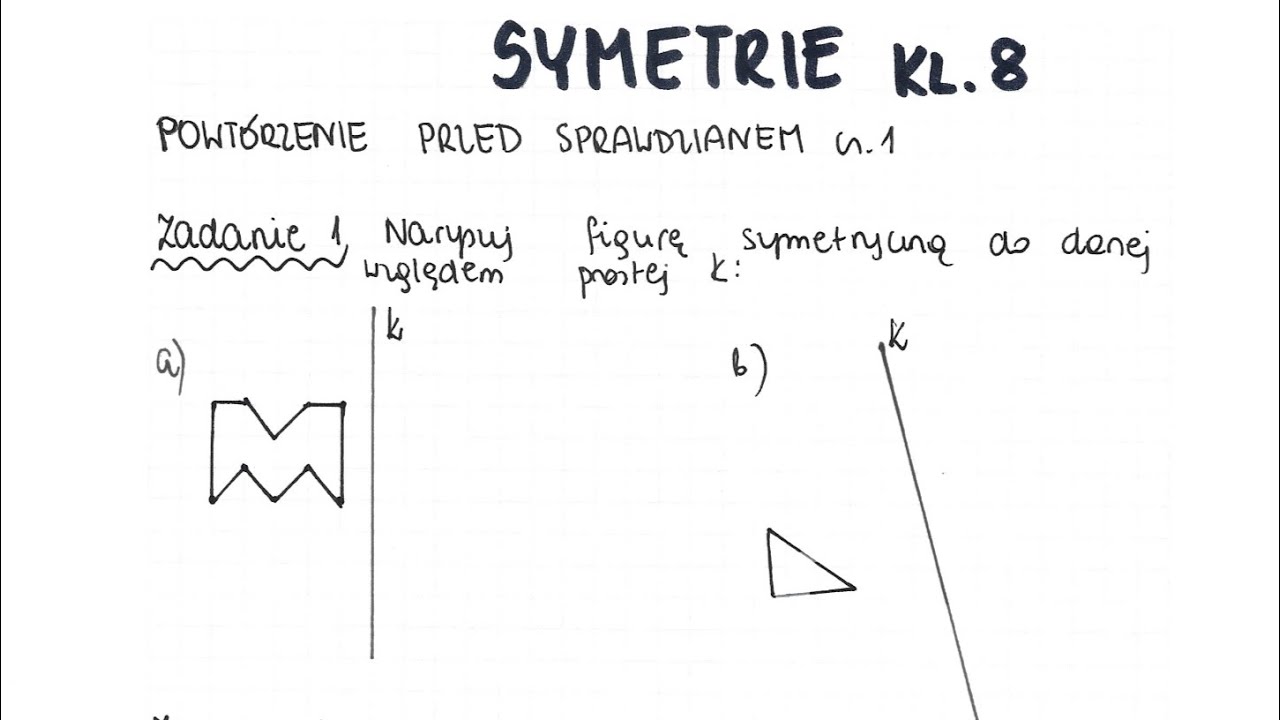
Konstrukcje symetryczne: Często trzeba będzie narysować figurę symetryczną do danej względem osi lub punktu. Pamiętajcie o tym, że odległość punktu od osi (lub środka) musi być taka sama jak odległość jego obrazu symetrycznego od tej osi (lub środka). Używajcie linijki i kątomierza, żeby zachować dokładność.
Określanie, czy figura ma oś/środek symetrii: Spróbujcie narysować linię (oś) lub zaznaczyć punkt (środek) i sprawdźcie, czy figura jest względem nich symetryczna. Czasami trzeba trochę pokombinować.
Zadania tekstowe: Przeczytajcie zadanie uważnie i spróbujcie wyobrazić sobie sytuację geometryczną. Narysujcie pomocniczy rysunek – to bardzo ułatwia rozwiązanie!

Kilka dodatkowych porad:

Ćwiczcie, ćwiczcie i jeszcze raz ćwiczcie! Rozwiążcie jak najwięcej zadań z podręcznika i zbioru zadań. Im więcej przykładów zobaczycie, tym łatwiej będzie Wam rozwiązywać zadania na sprawdzianie.
Uważajcie na szczegóły! Czasami drobny błąd w konstrukcji może zepsuć całe rozwiązanie.
Sprawdzajcie swoje odpowiedzi! Upewnijcie się, że figura, którą narysowaliście, jest rzeczywiście symetryczna do danej figury.

WAŻNE: Pamiętajcie, że figura może mieć więcej niż jedną oś symetrii (np. kwadrat ma 4 osie symetrii) lub środek symetrii (np. okrąg ma nieskończenie wiele środków symetrii – każdy punkt leżący w jego środku!).

Słówko o przekształceniach geometrycznych: Symetria osiowa i środkowa to przykłady przekształceń geometrycznych, które zachowują odległości i kąty. Innymi przykładami przekształceń geometrycznych są przesunięcie równoległe (translacja) i obrót.

Mamy nadzieję, że ten artykuł pomógł Wam zrozumieć zagadnienia związane z symetrią. Teraz spokojnie możecie podejść do sprawdzianu z matematyki z plusem i pokazać, na co Was stać! Powodzenia!