Sprawdzian Pole Figur Klasa 5

Czy czeka Cię sprawdzian z pól figur w klasie 5 i czujesz lekkie napięcie? Spokojnie! Ten artykuł jest stworzony właśnie dla Ciebie. Razem krok po kroku przejdziemy przez najważniejsze zagadnienia, abyś mógł/mogła z pewnością siebie podejść do tego wyzwania. Zapomnij o stresie – z nami pola figur staną się Twoimi sprzymierzeńcami!

Co Cię czeka na sprawdzianie?

Sprawdzian z pól figur w klasie 5 zazwyczaj skupia się na kilku podstawowych kształtach i ich wzorach na pole. Zrozumienie tych wzorów i umiejętność ich zastosowania to klucz do sukcesu. Na co warto zwrócić szczególną uwagę?

Figury, które musisz znać:

Kwadrat: Najprostszy z nich – wszystkie boki równe!
Prostokąt: Dwa boki krótsze i dwa dłuższe.
Równoległobok: Podobny do prostokąta, ale boki mogą być pochylone.
Trójkąt: Trzy boki i trzy kąty – wiele możliwości!
Trapez: Czworokąt z jedną parą boków równoległych.

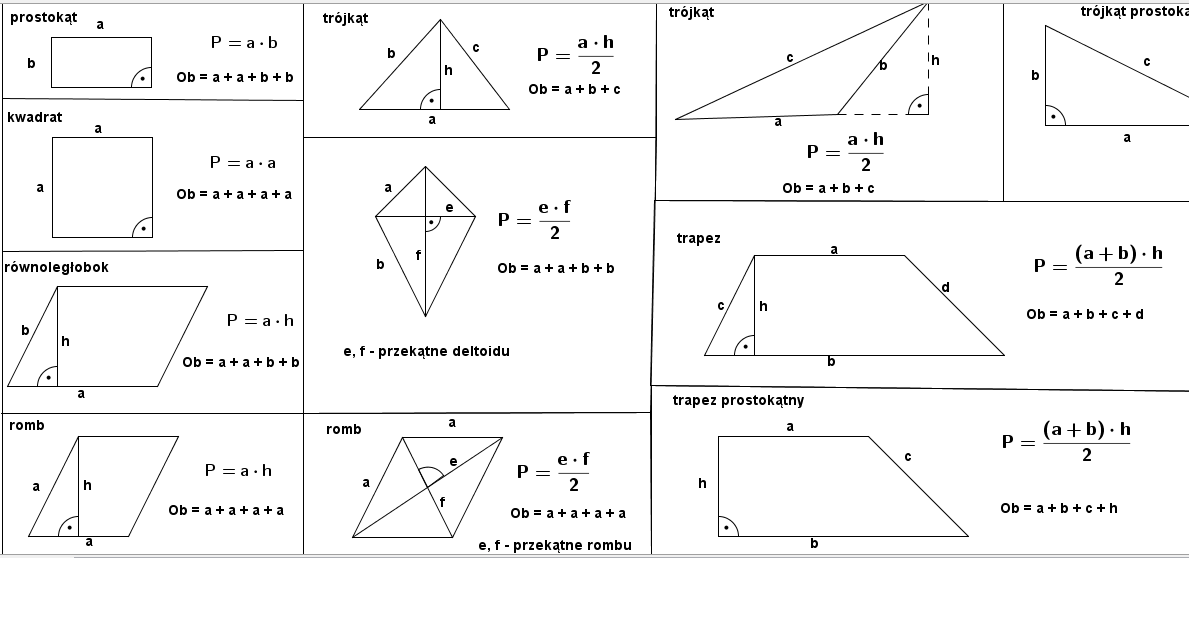
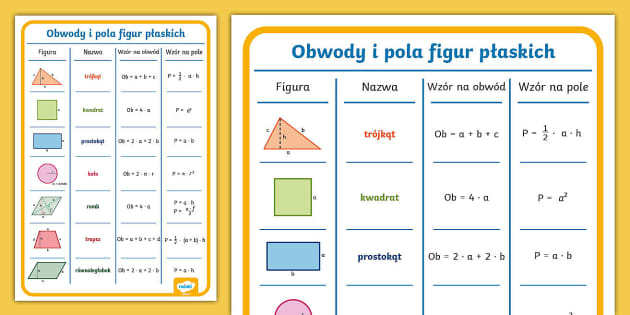
Wzory, które warto zapamiętać:

Kwadrat: Pole = bok * bok (a * a)
Prostokąt: Pole = bok * bok (a * b)
Równoległobok: Pole = podstawa * wysokość (a * h)
Trójkąt: Pole = (podstawa * wysokość) / 2 (a * h) / 2
Trapez: Pole = ((podstawa a + podstawa b) * wysokość) / 2 ((a + b) * h) / 2

Pamiętaj, że podstawa i wysokość w równoległoboku i trójkącie muszą być do siebie prostopadłe! To bardzo ważne, żeby nie pomylić ich z innymi bokami.

Jak się przygotować do sprawdzianu?

Najlepszym sposobem na przygotowanie jest systematyczna praca i rozwiązywanie zadań. Oto kilka wskazówek, które pomogą Ci skutecznie powtórzyć materiał:

Krok 1: Powtórz definicje i wzory.

Zanim zaczniesz rozwiązywać zadania, upewnij się, że dobrze rozumiesz definicje figur i znasz wzory na obliczanie ich pól. Zrób sobie kartkówkę i sprawdź, czy wszystko pamiętasz! Możesz nawet poprosić kogoś z rodziny, żeby Cię przepytał.

Krok 2: Rozwiązuj zadania krok po kroku.

Zacznij od prostych zadań, w których masz podane wszystkie potrzebne dane. Następnie przejdź do zadań bardziej złożonych, w których trzeba coś obliczyć wcześniej (np. wysokość trójkąta) lub wykorzystać kilka wzorów naraz. Nie poddawaj się, jeśli coś Ci nie wychodzi za pierwszym razem! Spróbuj jeszcze raz, a jeśli nadal masz problem, poproś o pomoc nauczyciela lub kolegę/koleżankę.

Krok 3: Zwróć uwagę na jednostki!

Jednostki są bardzo ważne! Jeśli masz podane długości boków w centymetrach (cm), to pole będzie wyrażone w centymetrach kwadratowych (cm²). Pamiętaj o tym i zawsze zapisuj jednostki w odpowiedzi.

Krok 4: Wizualizacja to podstawa!

Wyobraź sobie każdą figurę. Spróbuj narysować zadanie. Pomoże Ci to lepiej zrozumieć, co musisz obliczyć. Zaznacz na rysunku podstawę i wysokość. To naprawdę ułatwia sprawę!

Przykładowe zadania i ich rozwiązania

Żeby lepiej zrozumieć, jak stosować wzory, przeanalizujmy kilka przykładowych zadań:

Zadanie 1: Kwadrat

Oblicz pole kwadratu o boku długości 5 cm.

Rozwiązanie:

Wzór na pole kwadratu to P = a * a, gdzie a to długość boku. W tym przypadku a = 5 cm. Zatem P = 5 cm * 5 cm = 25 cm².

Odpowiedź: Pole kwadratu wynosi 25 cm².

Zadanie 2: Prostokąt

Oblicz pole prostokąta o bokach długości 8 cm i 3 cm.

Rozwiązanie:

Wzór na pole prostokąta to P = a * b, gdzie a i b to długości boków. W tym przypadku a = 8 cm i b = 3 cm. Zatem P = 8 cm * 3 cm = 24 cm².

Odpowiedź: Pole prostokąta wynosi 24 cm².

Zadanie 3: Równoległobok

Oblicz pole równoległoboku o podstawie długości 10 cm i wysokości opuszczonej na tę podstawę równej 4 cm.

Rozwiązanie:

Wzór na pole równoległoboku to P = a * h, gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę. W tym przypadku a = 10 cm i h = 4 cm. Zatem P = 10 cm * 4 cm = 40 cm².

Odpowiedź: Pole równoległoboku wynosi 40 cm².

Zadanie 4: Trójkąt

Oblicz pole trójkąta o podstawie długości 6 cm i wysokości opuszczonej na tę podstawę równej 7 cm.

Rozwiązanie:

Wzór na pole trójkąta to P = (a * h) / 2, gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę. W tym przypadku a = 6 cm i h = 7 cm. Zatem P = (6 cm * 7 cm) / 2 = 42 cm² / 2 = 21 cm².

Odpowiedź: Pole trójkąta wynosi 21 cm².

Zadanie 5: Trapez

Oblicz pole trapezu o podstawach długości 5 cm i 9 cm oraz wysokości równej 4 cm.

Rozwiązanie:

Wzór na pole trapezu to P = ((a + b) * h) / 2, gdzie a i b to długości podstaw, a h to wysokość. W tym przypadku a = 5 cm, b = 9 cm i h = 4 cm. Zatem P = ((5 cm + 9 cm) * 4 cm) / 2 = (14 cm * 4 cm) / 2 = 56 cm² / 2 = 28 cm².

Odpowiedź: Pole trapezu wynosi 28 cm².

Dodatkowe wskazówki

Czytaj uważnie treść zadania: Zwróć uwagę na to, co jest dane i co trzeba obliczyć. Czasami w treści zadania są ukryte dodatkowe informacje, które pomogą Ci w rozwiązaniu.
Sprawdzaj jednostki: Upewnij się, że wszystkie długości są podane w tych samych jednostkach (np. wszystkie w centymetrach). Jeśli nie, zamień je na te same jednostki przed rozpoczęciem obliczeń.
Rysuj schemat: Narysuj schemat figury, której pole masz obliczyć. Zaznacz na nim znane długości i kąty. To pomoże Ci lepiej zrozumieć zadanie i znaleźć właściwy wzór.
Sprawdzaj wynik: Po obliczeniu pola, sprawdź, czy wynik jest logiczny. Na przykład, pole kwadratu o boku 10 cm powinno być większe niż pole kwadratu o boku 5 cm.

Pamiętaj!

Matematyka to nie tylko wzory, ale przede wszystkim logiczne myślenie. Staraj się zrozumieć, dlaczego dany wzór działa i jak go stosować w różnych sytuacjach. Nie ucz się na pamięć – zrozum! To najlepszy sposób na sukces na sprawdzianie.

Powodzenia na sprawdzianie! Jesteśmy pewni, że dzięki temu artykułowi dasz radę! Pamiętaj, że najważniejsze to spokój i koncentracja. Przejrzyj zadania na spokojnie, zastosuj poznane wzory i uwierz w siebie!

Po sprawdzianie, niezależnie od wyniku, przeanalizuj swoje błędy i postaraj się je zrozumieć. To najlepszy sposób na naukę i rozwój. A przede wszystkim – nie zrażaj się! Matematyka może być naprawdę fascynująca, a każdy sprawdzian to kolejna okazja, żeby się czegoś nauczyć.