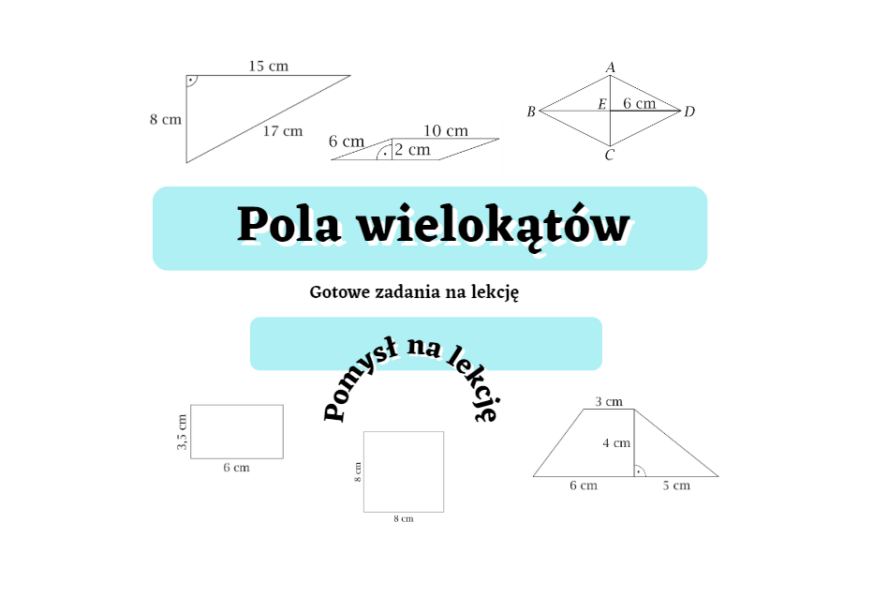
Sprawdzian Pola Wielokątów Klasa 6

Zapewne trafiłeś tutaj, ponieważ zbliża się sprawdzian z pól wielokątów w klasie 6. Rozumiem Twoje obawy! Matematyka, a zwłaszcza geometria, potrafi być wymagająca. Pamiętaj, że nie jesteś sam. Wielu uczniów ma trudności z tym tematem, a kluczem do sukcesu jest zrozumienie podstaw i regularne ćwiczenia.

Przygotowanie do tego sprawdzianu to nie tylko nauczenie się wzorów na pamięć. Chodzi o zrozumienie, *dlaczego* te wzory działają i jak je praktycznie zastosować. Wierzę, że z odpowiednim podejściem i pomocą, dasz radę!

Po co nam w ogóle te pola?

Może wydawać Ci się, że liczenie pól to tylko nudna teoria. Ale pomyśl o tym inaczej! Pola wielokątów otaczają nas z każdej strony:

• Pokój, w którym siedzisz ma powierzchnię – to pole prostokąta! Musisz to wiedzieć, np. kupując nową wykładzinę.
• Ogródek, który pielęgnujesz ma kształt trapezu, prostokąta lub innego wielokąta. Liczenie pól pomoże Ci obliczyć, ile trawy potrzebujesz.
• Planowanie remontu kuchni wymaga obliczenia powierzchni płytek.

To tylko kilka przykładów. Zrozumienie pól wielokątów to praktyczna umiejętność, która przydaje się w życiu codziennym! Nie uczysz się tego tylko na sprawdzian, ale nabywasz wiedzę, którą wykorzystasz w przyszłości.

Co musisz umieć?

Na sprawdzianie z pól wielokątów w klasie 6 najczęściej pojawiają się zadania dotyczące obliczania pól następujących figur:

1. Kwadrat

Kwadrat to najprostsza figura. Ma cztery równe boki i cztery kąty proste. Jego pole obliczamy, mnożąc długość boku przez siebie:

Pole kwadratu = a * a = a²

Gdzie 'a' to długość boku kwadratu.

Przykład: Kwadrat ma bok długości 5 cm. Jego pole to 5 cm * 5 cm = 25 cm².

2. Prostokąt

Prostokąt ma dwie pary równych boków i cztery kąty proste. Jego pole obliczamy, mnożąc długość jednego boku przez długość drugiego:

Pole prostokąta = a * b

Gdzie 'a' i 'b' to długości boków prostokąta.

Przykład: Prostokąt ma boki długości 8 cm i 3 cm. Jego pole to 8 cm * 3 cm = 24 cm².

3. Równoległobok

Równoległobok ma dwie pary równoległych boków. Jego pole obliczamy, mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę:

Pole równoległoboku = a * h

Gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę.

Pamiętaj! Wysokość musi być prostopadła do podstawy.

Przykład: Równoległobok ma podstawę długości 10 cm i wysokość opuszczoną na tę podstawę długości 4 cm. Jego pole to 10 cm * 4 cm = 40 cm².

4. Romb

Romb to szczególny przypadek równoległoboku. Ma wszystkie boki równe. Można więc obliczyć jego pole, tak jak pole równoległoboku: a * h. Ale romb ma również przekątne, które przecinają się pod kątem prostym. Możemy więc skorzystać z innego wzoru:

Pole rombu = (d₁ * d₂) / 2

Gdzie 'd₁' i 'd₂' to długości przekątnych rombu.

Przykład: Romb ma przekątne długości 6 cm i 8 cm. Jego pole to (6 cm * 8 cm) / 2 = 24 cm².

5. Trójkąt

Pole trójkąta obliczamy, mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę i dzieląc wynik przez 2:

Pole trójkąta = (a * h) / 2

Gdzie 'a' to długość podstawy, a 'h' to wysokość opuszczona na tę podstawę.

Pamiętaj! Wysokość musi być prostopadła do podstawy.

Przykład: Trójkąt ma podstawę długości 7 cm i wysokość opuszczoną na tę podstawę długości 5 cm. Jego pole to (7 cm * 5 cm) / 2 = 17,5 cm².

6. Trapez

Trapez ma dwie podstawy (równoległe do siebie) i dwie ramiona. Jego pole obliczamy, dodając długości podstaw, mnożąc sumę przez wysokość i dzieląc wynik przez 2:

Pole trapezu = ((a + b) * h) / 2

Gdzie 'a' i 'b' to długości podstaw, a 'h' to wysokość trapezu (odległość między podstawami).

Przykład: Trapez ma podstawy długości 5 cm i 9 cm oraz wysokość 4 cm. Jego pole to ((5 cm + 9 cm) * 4 cm) / 2 = 28 cm².

Typowe zadania na sprawdzianie

Na sprawdzianie możesz spodziewać się różnych typów zadań. Oto kilka przykładów:

• Obliczanie pola figury, mając podane długości boków/podstaw/wysokości/przekątnych.
• Obliczanie długości boku/podstawy/wysokości, mając podane pole i inne wymiary figury.
• Porównywanie pól dwóch figur.
• Zadania tekstowe, w których trzeba wyodrębnić informacje potrzebne do obliczenia pola.
• Dzielenie figury na mniejsze, prostsze figury i obliczanie pola każdej z nich, a następnie sumowanie pól.

Jak się przygotować?

Najlepszym sposobem na przygotowanie do sprawdzianu jest:

• Powtórzenie teorii – upewnij się, że znasz wzory na pola wszystkich figur.
• Rozwiązywanie zadań – im więcej zadań rozwiążesz, tym lepiej zrozumiesz, jak stosować wzory w praktyce. Korzystaj z podręcznika, zeszytu ćwiczeń i internetu.
• Analiza błędów – jeśli popełnisz błąd, postaraj się zrozumieć, dlaczego to się stało. Zapytaj nauczyciela lub kolegów o pomoc.
• Praca w grupie – wspólnie z innymi uczniami możecie rozwiązywać zadania, tłumaczyć sobie trudne zagadnienia i wzajemnie się motywować.
• Odpoczynek – pamiętaj o regularnym odpoczynku. Przemęczony umysł trudniej przyswaja wiedzę.

Częste błędy i jak ich unikać

Wielu uczniów popełnia podobne błędy na sprawdzianach z pól wielokątów. Oto kilka z nich i wskazówki, jak ich unikać:

• Pomylenie wzorów – Upewnij się, że znasz wzory na pamięć i wiesz, kiedy który zastosować. Dobrym sposobem jest wypisanie wszystkich wzorów na kartce i porównywanie ich.
• Nieuważne czytanie treści zadania – Zawsze dokładnie czytaj treść zadania. Zwróć uwagę na jednostki miar i na to, co jest szukane. Podkreśl najważniejsze informacje.
• Zapominanie o jednostkach – Pamiętaj o podawaniu jednostek pola (np. cm², m²).
• Błędy rachunkowe – Sprawdzaj swoje obliczenia. Możesz użyć kalkulatora, ale pamiętaj, że na sprawdzianie może go nie być.
• Niezrozumienie pojęcia wysokości – Pamiętaj, że wysokość musi być *prostopadła* do podstawy. Często w zadaniach podawana jest długość boku, który nie jest wysokością.

Alternatywne punkty widzenia

Niektórzy uważają, że nauka pól wielokątów jest bezcelowa, ponieważ w dzisiejszych czasach wszystko można obliczyć za pomocą komputerów i specjalnych programów. Jednak zrozumienie zasad geometrii pozwala na krytyczne myślenie i rozwiązywanie problemów w różnych dziedzinach życia. Komputer jest tylko narzędziem, a Ty musisz wiedzieć, jak go użyć i czy wynik, który otrzymujesz, jest sensowny. Poza tym, liczenie pól rozwija wyobraźnię przestrzenną, co jest przydatne w wielu zawodach, np. architekta, projektanta, inżyniera.

Pamiętaj o pozytywnym nastawieniu!

Wiara w siebie to podstawa! Nie zrażaj się, jeśli coś Ci nie wychodzi. Każdy uczeń uczy się w swoim tempie. Najważniejsze to nie poddawać się i regularnie pracować. Wykorzystaj ten czas na zrozumienie materiału, a nie tylko na jego zapamiętanie. Zrozumienie to klucz do sukcesu.

Mam nadzieję, że ten artykuł pomógł Ci w przygotowaniu do sprawdzianu z pól wielokątów. Powodzenia!

Czy po przeczytaniu tego artykułu czujesz się pewniej w obliczaniu pól wielokątów? Jakie konkretne działania podejmiesz, aby jeszcze lepiej przygotować się do sprawdzianu?