Sprawdzian Pola Figur Klasa 6

Zastanawiasz się, jak skutecznie przygotować się do sprawdzianu z pól figur w klasie 6? A może jesteś rodzicem, który chce pomóc swojemu dziecku w zrozumieniu tego zagadnienia? Ten artykuł jest właśnie dla Ciebie! Skupimy się na najważniejszych aspektach, dzięki którym opanowanie obliczania pól figur stanie się prostsze i przyjemniejsze. Przygotuj się na solidną dawkę wiedzy, praktycznych wskazówek i przykładów, które pomogą Ci zabłysnąć na sprawdzianie!

Wstęp do Świata Pól Figur

Pola figur to jedno z kluczowych zagadnień w geometrii. Zrozumienie, jak obliczać pola różnych kształtów, jest niezbędne nie tylko do zaliczenia sprawdzianu, ale również do rozwiązywania praktycznych problemów w życiu codziennym. Pomyśl o malowaniu pokoju, obliczaniu powierzchni trawnika, czy planowaniu ogrodu – we wszystkich tych sytuacjach znajomość pól figur jest nieoceniona.

Dlaczego Pola Figur Są Ważne?

Praktyczne Zastosowania: Jak wspomniano, wiedza o polach figur przydaje się w wielu sytuacjach życiowych.
Podstawa Geometrii: Rozumienie pól figur stanowi fundament do dalszej nauki geometrii, w tym objętości brył.
Rozwój Myślenia Logicznego: Obliczanie pól figur wymaga logicznego myślenia i rozwiązywania problemów.

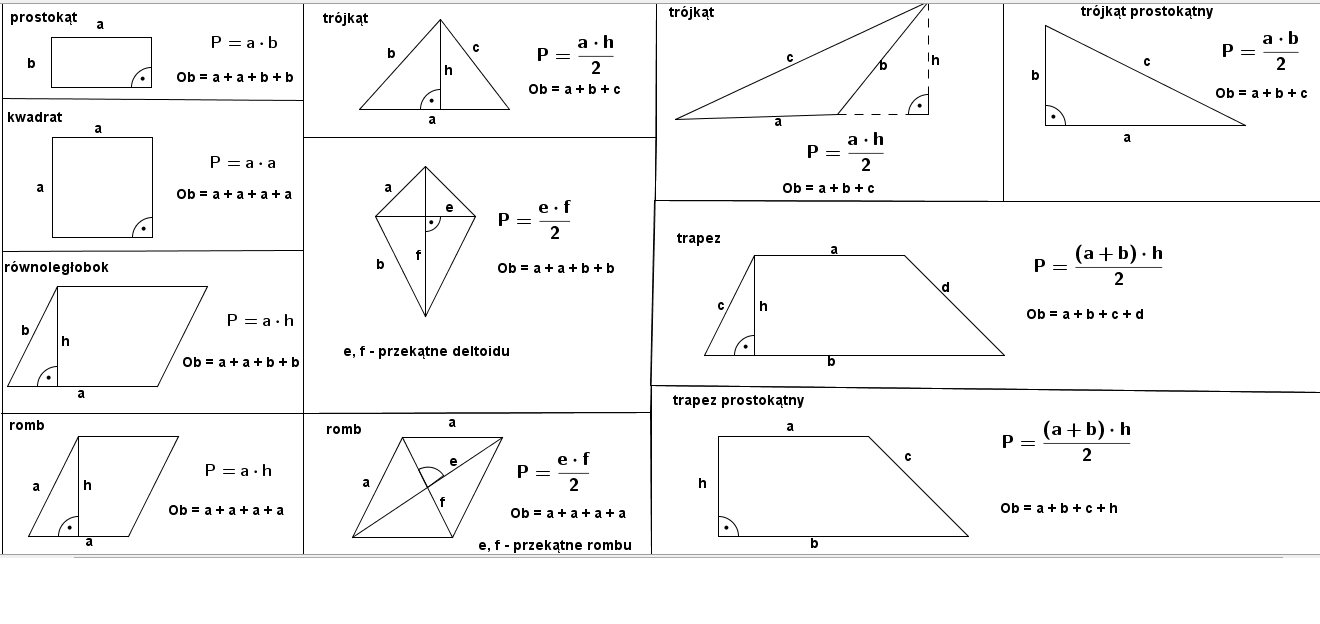
Podstawowe Figury i Wzory

Zacznijmy od przypomnienia sobie wzorów na pola podstawowych figur, które najczęściej pojawiają się na sprawdzianach w klasie 6. Pamiętaj, że znajomość wzorów to podstawa sukcesu!

Kwadrat

Kwadrat to figura, która ma wszystkie boki równe. Pole kwadratu obliczamy, mnożąc długość boku przez siebie.

Wzór: P = a * a = a²

Gdzie: a – długość boku kwadratu

Przykład: Jeśli bok kwadratu ma długość 5 cm, to jego pole wynosi 5 cm * 5 cm = 25 cm².

Prostokąt

Prostokąt ma boki parami równe. Pole prostokąta obliczamy, mnożąc długość jednego boku przez długość drugiego boku.

Wzór: P = a * b

Gdzie: a – długość jednego boku, b – długość drugiego boku

Przykład: Jeśli jeden bok prostokąta ma długość 8 cm, a drugi 4 cm, to jego pole wynosi 8 cm * 4 cm = 32 cm².

Trójkąt

Obliczanie pola trójkąta jest nieco bardziej skomplikowane, ale z odpowiednim wzorem staje się proste. Najczęściej korzystamy ze wzoru, w którym potrzebujemy długości podstawy i wysokości.

Wzór: P = (a * h) / 2

Gdzie: a – długość podstawy trójkąta, h – wysokość trójkąta (odcinek prostopadły do podstawy, łączący podstawę z wierzchołkiem)

Przykład: Jeśli podstawa trójkąta ma długość 6 cm, a wysokość 5 cm, to jego pole wynosi (6 cm * 5 cm) / 2 = 15 cm².

Równoległobok

Równoległobok to czworokąt, który ma dwie pary boków równoległych. Pole równoległoboku obliczamy, mnożąc długość podstawy przez wysokość opuszczoną na tę podstawę.

Wzór: P = a * h

Gdzie: a – długość podstawy równoległoboku, h – wysokość równoległoboku (odcinek prostopadły do podstawy, łączący podstawę z przeciwległym bokiem)

Przykład: Jeśli podstawa równoległoboku ma długość 7 cm, a wysokość 3 cm, to jego pole wynosi 7 cm * 3 cm = 21 cm².

Romb

Romb to równoległobok, który ma wszystkie boki równe. Możemy obliczyć jego pole tak samo jak równoległoboku, ale mamy też inny wzór, wykorzystujący długości przekątnych.

Wzór 1: P = a * h (tak jak równoległobok)

Wzór 2: P = (d₁ * d₂) / 2

Gdzie: a – długość boku rombu, h – wysokość rombu, d₁ – długość jednej przekątnej, d₂ – długość drugiej przekątnej

Przykład: Jeśli przekątne rombu mają długości 8 cm i 6 cm, to jego pole wynosi (8 cm * 6 cm) / 2 = 24 cm².

Trapez

Trapez to czworokąt, który ma przynajmniej jedną parę boków równoległych. Boki równoległe nazywamy podstawami trapezu. Pole trapezu obliczamy, dodając długości podstaw, mnożąc przez wysokość i dzieląc przez 2.

Wzór: P = ((a + b) * h) / 2

Gdzie: a – długość jednej podstawy trapezu, b – długość drugiej podstawy trapezu, h – wysokość trapezu (odcinek prostopadły do podstaw, łączący obie podstawy)

Przykład: Jeśli podstawy trapezu mają długości 5 cm i 9 cm, a wysokość 4 cm, to jego pole wynosi ((5 cm + 9 cm) * 4 cm) / 2 = 28 cm².

Praktyczne Wskazówki i Triki

Znajomość wzorów to dopiero początek. Ważne jest również, aby potrafić zastosować je w praktyce. Oto kilka wskazówek, które pomogą Ci rozwiązywać zadania ze sprawdzianu:

Zrozum Treść Zadania: Zanim zaczniesz liczyć, dokładnie przeczytaj zadanie! Upewnij się, że rozumiesz, o co pytają i jakie dane masz podane.
Narysuj Rysunek Pomocniczy: Rysunek pomoże Ci zwizualizować problem i zidentyfikować potrzebne dane.
Wybierz Odpowiedni Wzór: Zastanów się, jaki wzór jest najbardziej odpowiedni do danej figury i danych w zadaniu.
Pamiętaj o Jednostkach: Zawsze zapisuj jednostki (np. cm², m²) przy wyniku!
Sprawdź Wynik: Po obliczeniu pola, sprawdź, czy wynik jest sensowny. Czy pole figury może być ujemne? Czy pole bardzo małej figury może być ogromne?

Zadania z życia wzięte

Sprawdźmy, jak możemy wykorzystać wiedzę o polach figur w praktycznych sytuacjach:

Zadanie 1: Dywan w Pokoju

Asia chce kupić dywan do swojego pokoju, który ma kształt prostokąta o wymiarach 3 m na 4 m. Ile metrów kwadratowych dywanu potrzebuje Asia?

Rozwiązanie:

Pokój ma kształt prostokąta, więc używamy wzoru na pole prostokąta: P = a * b. W tym przypadku a = 3 m, b = 4 m. Zatem P = 3 m * 4 m = 12 m². Asia potrzebuje 12 metrów kwadratowych dywanu.

Zadanie 2: Ogródek w Kształcie Trójkąta

Pan Kowalski ma ogródek w kształcie trójkąta. Podstawa trójkąta ma długość 10 m, a wysokość opuszczona na tę podstawę ma długość 8 m. Jakie jest pole tego ogródka?

Rozwiązanie:

Ogródek ma kształt trójkąta, więc używamy wzoru na pole trójkąta: P = (a * h) / 2. W tym przypadku a = 10 m, h = 8 m. Zatem P = (10 m * 8 m) / 2 = 40 m². Pole ogródka wynosi 40 metrów kwadratowych.

Zadanie 3: Dach w Kształcie Trapezu

Dach domu ma kształt trapezu. Długości podstaw trapezu wynoszą 6 m i 8 m, a wysokość trapezu wynosi 3 m. Jakie jest pole powierzchni dachu?

Rozwiązanie:

Dach ma kształt trapezu, więc używamy wzoru na pole trapezu: P = ((a + b) * h) / 2. W tym przypadku a = 6 m, b = 8 m, h = 3 m. Zatem P = ((6 m + 8 m) * 3 m) / 2 = 21 m². Pole powierzchni dachu wynosi 21 metrów kwadratowych.

Częste Błędy i Jak Ich Unikać

Podczas rozwiązywania zadań z pól figur, uczniowie często popełniają te same błędy. Oto kilka z nich i sposoby, jak ich unikać:

Pomylenie Wzorów: Ucz się wzorów na pamięć i regularnie powtarzaj. Możesz przygotować sobie kartkę ze wzorami i mieć ją zawsze pod ręką podczas rozwiązywania zadań.
Złe Podstawienie Danych: Upewnij się, że podstawiasz odpowiednie wartości do wzoru. Narysuj rysunek i zaznacz na nim dane, żeby łatwiej było je zidentyfikować.
Zapominanie o Jednostkach: Zawsze pamiętaj o zapisywaniu jednostek! Jeśli wynik podasz bez jednostki, nauczyciel może obniżyć ocenę.
Błędy w Obliczeniach: Uważnie wykonuj obliczenia. Jeśli masz trudności z liczeniem w pamięci, użyj kalkulatora.
Brak Sprawdzenia Wyniku: Po obliczeniu pola, sprawdź, czy wynik jest sensowny. Zastanów się, czy pole figury może być ujemne, czy jest zbyt duże lub zbyt małe w stosunku do wymiarów figury.

Dodatkowe Materiały i Ćwiczenia

Oprócz tego artykułu, warto skorzystać z innych materiałów, które pomogą Ci w przygotowaniu do sprawdzianu. Możesz poszukać ćwiczeń w podręczniku, zeszycie ćwiczeń, lub w internecie. Im więcej ćwiczysz, tym lepiej!

Podręcznik: Przejrzyj rozdział o polach figur i rozwiąż wszystkie zadania.
Zeszyt Ćwiczeń: Zeszyt ćwiczeń zawiera dodatkowe zadania, które pomogą Ci utrwalić wiedzę.
Internet: W internecie znajdziesz wiele stron z zadaniami z geometrii. Możesz również poszukać filmików instruktażowych, które tłumaczą, jak obliczać pola figur.
Korepetycje: Jeśli masz trudności z geometrią, możesz poprosić o pomoc korepetytora.

Podsumowanie i Zachęta do Dalszej Pracy

Gratulacje! Dotarliśmy do końca artykułu. Mam nadzieję, że teraz czujesz się pewniej w temacie obliczania pól figur. Pamiętaj, że kluczem do sukcesu jest regularna nauka, rozwiązywanie zadań i korzystanie z różnych źródeł wiedzy. Nie zrażaj się trudnościami – każda przeszkoda to szansa na rozwój!

Życzę Ci powodzenia na sprawdzianie! Pamiętaj, że wiedza o polach figur to nie tylko sprawdzian, ale również umiejętność, która przyda Ci się w życiu. Baw się dobrze, odkrywając fascynujący świat geometrii!

Powodzenia!