Sprawdzian Pola Figur Klasa 5 Nowa Era

Czy Twój uczeń klasy 5 przygotowuje się do sprawdzianu z pól figur, a Ty czujesz lekką panikę? Spokojnie! Ten artykuł jest dla Ciebie – rodzica, opiekuna lub nauczyciela, który pragnie wesprzeć młodego matematyka w opanowaniu tego zagadnienia. Skupimy się na materiale zawartym w podręcznikach i zeszytach ćwiczeń wydawnictwa Nowa Era, ale przedstawimy go w sposób przystępny, praktyczny i pełen przydatnych wskazówek.

Wiemy, że matematyka, zwłaszcza w szkole podstawowej, bywa postrzegana jako trudna i abstrakcyjna. Chcemy to zmienić! Naszym celem jest pokazanie, że obliczanie pól figur może być fascynującą przygodą, a zrozumienie zasad – kluczem do sukcesu na sprawdzianie i w dalszej edukacji.

Czym jest Pole Figury i Dlaczego Jest Ważne?

Pole figury to, najprościej mówiąc, miara powierzchni, jaką zajmuje dana figura na płaszczyźnie. Wyobraź sobie, że malujesz ścianę. Pole figury to ilość farby, której potrzebujesz, żeby ją całą pokryć. Zrozumienie tego pojęcia jest fundamentem do dalszej nauki geometrii i matematyki.

Dlaczego jest to takie ważne?

Praktyczne zastosowanie: Obliczanie powierzchni pokoju przy remoncie, obliczanie zużycia materiału przy szyciu, planowanie ogrodu – to tylko niektóre z przykładów z życia codziennego.
Kolejne etapy edukacji: Wiedza o polach figur jest niezbędna w geometrii, trygonometrii i analizie matematycznej w późniejszych klasach i na studiach.
Rozwijanie logicznego myślenia: Obliczanie pól figur wymaga logicznego myślenia, analizowania danych i stosowania odpowiednich wzorów.

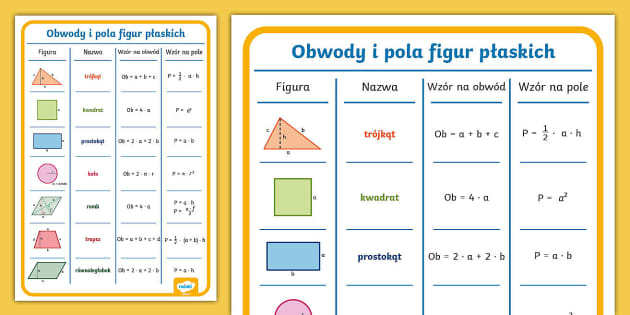
Figury, Które Pojawiają się na Sprawdzianie – Nowa Era Klasa 5

Podręczniki i zeszyty ćwiczeń Nowej Ery dla klasy 5 zazwyczaj koncentrują się na kilku podstawowych figurach. Znamy je dobrze:

Kwadrat
Prostokąt
Równoległobok
Romb
Trójkąt (różne rodzaje)
Trapez

Omówimy każdą z tych figur, przedstawiając wzory na obliczanie ich pól i dając praktyczne przykłady.

Kwadrat i Prostokąt – Podstawy Geometrii

Kwadrat: To czworokąt, który ma wszystkie boki równe i wszystkie kąty proste. Pole kwadratu obliczamy, mnożąc długość boku przez samą siebie (a * a = a²). Przykład: Kwadrat ma bok długości 5 cm. Jego pole wynosi 5 cm * 5 cm = 25 cm².

Prostokąt: To czworokąt, który ma wszystkie kąty proste, ale boki nie muszą być równe. Pole prostokąta obliczamy, mnożąc długość jednego boku (a) przez długość drugiego boku (b) (a * b). Przykład: Prostokąt ma boki długości 7 cm i 3 cm. Jego pole wynosi 7 cm * 3 cm = 21 cm².

Pamiętajmy o jednostkach! Zawsze podajemy pole w jednostkach kwadratowych (cm², m², km² itd.).

Równoległobok i Romb – Trochę Więcej Wyzwań

Równoległobok: To czworokąt, który ma dwie pary boków równoległych. Pole równoległoboku obliczamy, mnożąc długość podstawy (a) przez wysokość (h) opuszczoną na tę podstawę (a * h). Wysokość to odległość między dwiema równoległymi podstawami! Przykład: Równoległobok ma podstawę długości 8 cm i wysokość opuszczoną na tę podstawę długości 4 cm. Jego pole wynosi 8 cm * 4 cm = 32 cm².

Romb: To równoległobok, który ma wszystkie boki równe. Możemy obliczyć jego pole tak samo jak pole równoległoboku (a * h), ale romb ma jeszcze jedną specjalną metodę. Pole rombu możemy również obliczyć, mnożąc długości jego przekątnych (e i f) i dzieląc wynik przez 2 ((e * f) / 2). Przykład: Romb ma przekątne długości 6 cm i 10 cm. Jego pole wynosi (6 cm * 10 cm) / 2 = 30 cm².

Trójkąt – Podstawa Geometrii

Trójkąt: To figura, która ma trzy boki i trzy kąty. Pole trójkąta obliczamy, mnożąc długość podstawy (a) przez wysokość (h) opuszczoną na tę podstawę i dzieląc wynik przez 2 ((a * h) / 2). Wysokość trójkąta to odległość od wierzchołka do podstawy (lub jej przedłużenia) prostopadła do tej podstawy. Przykład: Trójkąt ma podstawę długości 9 cm i wysokość opuszczoną na tę podstawę długości 6 cm. Jego pole wynosi (9 cm * 6 cm) / 2 = 27 cm².

Ważne! W trójkącie prostokątnym, dwa boki tworzące kąt prosty są jednocześnie podstawą i wysokością.

Trapez – Ostatni Krok

Trapez: To czworokąt, który ma co najmniej jedną parę boków równoległych (zwanych podstawami). Pole trapezu obliczamy, dodając długości podstaw (a i b), mnożąc wynik przez wysokość (h) (odległość między podstawami) i dzieląc wszystko przez 2 (((a + b) * h) / 2). Przykład: Trapez ma podstawy długości 5 cm i 7 cm oraz wysokość 4 cm. Jego pole wynosi ((5 cm + 7 cm) * 4 cm) / 2 = 24 cm².

Jak Skutecznie Przygotować się do Sprawdzianu? – Porady i Wskazówki

Oto kilka praktycznych wskazówek, które pomogą Twojemu dziecku w przygotowaniach:

Powtórz wzory: Stwórz listę wszystkich wzorów na pola figur i upewnij się, że uczeń je rozumie i pamięta. Można użyć fiszek, aplikacji mobilnych lub po prostu przepisywać wzory kilka razy.
Rozwiąż zadania: Im więcej zadań rozwiąże uczeń, tym lepiej zrozumie zasady i nabierze wprawy. Zacznij od prostych zadań z podręcznika i zeszytu ćwiczeń, a następnie przejdź do trudniejszych.
Zrozumienie, a nie wkuwanie: Najważniejsze jest zrozumienie, dlaczego dany wzór działa, a nie tylko bezmyślne wkuwanie go na pamięć. Spróbuj wyjaśnić wzory w sposób obrazowy, używając przykładów z życia codziennego.
Rysuj! Zawsze rysuj figury, o których mowa w zadaniu. To pomoże uczniowi lepiej zrozumieć problem i zidentyfikować potrzebne dane.
Sprawdzaj jednostki: Zwróć uwagę na to, żeby uczeń zawsze podawał wynik w odpowiednich jednostkach kwadratowych (cm², m², km² itd.).
Praca z podręcznikiem Nowej Ery: Skup się na zadaniach i przykładach zawartych w podręczniku i zeszycie ćwiczeń Nowej Ery. Sprawdzian prawdopodobnie będzie oparty na tym materiale.
Ćwiczenia online: Skorzystaj z dostępnych online zasobów i generatorów zadań z geometrii. Wiele stron oferuje interaktywne ćwiczenia, które mogą być bardzo pomocne.
Przerwy! Regularne przerwy podczas nauki są bardzo ważne. Pozwalają mózgowi odpocząć i lepiej przyswajać informacje.
Pozytywne nastawienie: Zachęcaj ucznia i chwal go za postępy. Pozytywne nastawienie to połowa sukcesu!

Przykładowe Zadania i Rozwiązania – Zbliżamy Się do Metodyki Nowej Ery

Oto kilka przykładowych zadań, które mogą pojawić się na sprawdzianie, wraz z rozwiązaniami:

Zadanie 1: Oblicz pole kwadratu o boku długości 8 cm.
Rozwiązanie: Pole kwadratu = a² = 8 cm * 8 cm = 64 cm²
Zadanie 2: Oblicz pole prostokąta o bokach długości 12 cm i 5 cm.
Rozwiązanie: Pole prostokąta = a * b = 12 cm * 5 cm = 60 cm²
Zadanie 3: Oblicz pole trójkąta o podstawie długości 10 cm i wysokości opuszczonej na tę podstawę długości 7 cm.
Rozwiązanie: Pole trójkąta = (a * h) / 2 = (10 cm * 7 cm) / 2 = 35 cm²
Zadanie 4: Oblicz pole trapezu o podstawach długości 6 cm i 9 cm oraz wysokości 4 cm.
Rozwiązanie: Pole trapezu = ((a + b) * h) / 2 = ((6 cm + 9 cm) * 4 cm) / 2 = 30 cm²
Zadanie 5: Oblicz pole rombu, którego przekątne mają długości 8 cm i 12 cm.
Rozwiązanie: Pole rombu = (e * f) / 2 = (8 cm * 12 cm) / 2 = 48 cm²

Wskazówka: Zwróć uwagę na to, żeby uczeń zapisywał jednostki miar przy każdym etapie obliczeń. To pomoże uniknąć błędów.

Dodatkowe Materiały i Zasoby

Oprócz podręcznika i zeszytu ćwiczeń Nowej Ery, warto skorzystać z dodatkowych materiałów edukacyjnych:

Strony internetowe: Istnieje wiele stron internetowych oferujących darmowe materiały do nauki matematyki, w tym zadania, testy i filmy edukacyjne.
Aplikacje mobilne: W App Store i Google Play można znaleźć aplikacje mobilne do nauki geometrii, które są interaktywne i angażujące.
Książki z zadaniami: Można kupić dodatkowe książki z zadaniami z geometrii, które oferują więcej ćwiczeń i wyzwań.
Korepetycje: Jeśli uczeń ma duże trudności z opanowaniem materiału, warto rozważyć korepetycje z matematyki.

Podsumowanie – Klucz do Sukcesu

Przygotowanie do sprawdzianu z pól figur w klasie 5 wymaga systematyczności, zrozumienia zasad i praktyki. Pamiętaj, że najważniejsze jest, żeby uczeń zrozumiał, dlaczego dany wzór działa, a nie tylko bezmyślnie wkuwał go na pamięć. Wykorzystaj materiały zawarte w podręcznikach i zeszytach ćwiczeń Nowej Ery, a także dodatkowe zasoby edukacyjne. Wspieraj ucznia, chwal go za postępy i twórz pozytywną atmosferę podczas nauki.

Mamy nadzieję, że ten artykuł był dla Ciebie pomocny. Życzymy powodzenia na sprawdzianie!