Sprawdzian Pola Figur Klasa 5

Zbliża się sprawdzian z pól figur w klasie 5 i czujesz lekkie napięcie? To zupełnie normalne! Wielu uczniów ma podobne odczucia przed sprawdzianem. Pamiętaj, że praktyka czyni mistrza, a odpowiednie przygotowanie to klucz do sukcesu. Ten artykuł pomoże Ci uporządkować wiedzę i poczuć się pewniej. Zrozumienie pól figur to nie tylko kolejny temat w szkole – ma on realny wpływ na Twoje codzienne życie.

Dlaczego pola figur są ważne?

Możesz się zastanawiać, po co właściwie uczyć się o polach figur. Odpowiedź jest prosta: pola figur otaczają nas wszędzie!

Remont pokoju: Obliczając ilość potrzebnej farby do pomalowania ściany, korzystasz z wiedzy o polu prostokąta.
Zakupy: Porównując powierzchnię dwóch pizz o różnych cenach, możesz ocenić, która oferta jest bardziej opłacalna.
Ogród: Planując rabatki kwiatowe, potrzebujesz wiedzieć, ile miejsca zajmie każda roślina.
Szycie: Krojąc materiał na ubranie, obliczasz powierzchnię poszczególnych elementów.

Jak widzisz, umiejętność obliczania pól figur przydaje się w wielu sytuacjach życiowych. To nie tylko teoria, ale przede wszystkim praktyczne narzędzie.

Podstawowe figury i ich pola

Spójrzmy teraz na podstawowe figury, których pola będziesz musiał znać na sprawdzianie:

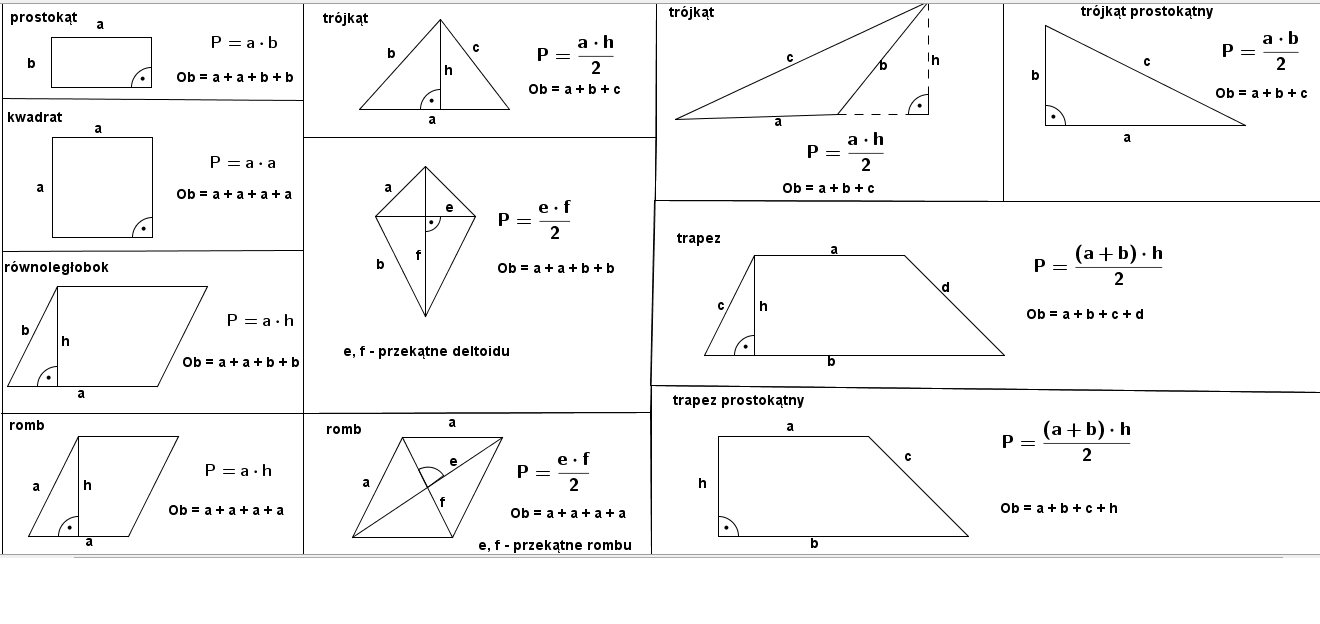
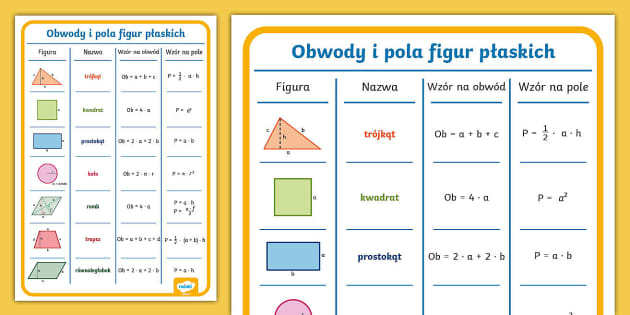
Prostokąt

Prostokąt to figura, która ma cztery kąty proste i przeciwległe boki równej długości. Jego pole obliczamy, mnożąc długość jednego boku (a) przez długość drugiego boku (b):

Pole prostokąta: P = a * b

Przykład: Prostokąt ma boki długości 5 cm i 8 cm. Jego pole wynosi 5 cm * 8 cm = 40 cm².

Kwadrat

Kwadrat to szczególny przypadek prostokąta, w którym wszystkie boki są równe. Oznaczamy długość boku kwadratu jako a. Jego pole obliczamy:

Pole kwadratu: P = a * a = a²

Przykład: Kwadrat ma bok długości 6 cm. Jego pole wynosi 6 cm * 6 cm = 36 cm².

Równoległobok

Równoległobok ma dwie pary boków równoległych. Jego pole obliczamy, mnożąc długość podstawy (a) przez wysokość (h) opuszczoną na tę podstawę:

Pole równoległoboku: P = a * h

Przykład: Równoległobok ma podstawę długości 10 cm i wysokość opuszczoną na tę podstawę równą 4 cm. Jego pole wynosi 10 cm * 4 cm = 40 cm².

Trójkąt

Trójkąt to figura o trzech bokach. Jego pole obliczamy, mnożąc długość podstawy (a) przez wysokość (h) opuszczoną na tę podstawę, a następnie dzieląc wynik przez 2:

Pole trójkąta: P = (a * h) / 2

Przykład: Trójkąt ma podstawę długości 7 cm i wysokość opuszczoną na tę podstawę równą 5 cm. Jego pole wynosi (7 cm * 5 cm) / 2 = 17.5 cm².

Trapez

Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych (zwanych podstawami). Jego pole obliczamy, dodając długości podstaw (a i b), mnożąc sumę przez wysokość (h), a następnie dzieląc wynik przez 2:

Pole trapezu: P = ((a + b) * h) / 2

Przykład: Trapez ma podstawy długości 6 cm i 8 cm, a wysokość równą 3 cm. Jego pole wynosi ((6 cm + 8 cm) * 3 cm) / 2 = 21 cm².

Wskazówki i triki

Oto kilka wskazówek, które pomogą Ci lepiej przygotować się do sprawdzianu:

Zapamiętaj wzory: Zapisz wzory na kartce i powtarzaj je regularnie. Możesz też spróbować wymyślić rymowanki, które pomogą Ci je zapamiętać.
Rysuj figury: Zawsze rysuj figury, jeśli treść zadania tego nie robi. Pomoże Ci to lepiej zrozumieć zadanie i zidentyfikować potrzebne dane.
Podstawiaj wartości: Po narysowaniu figury, zapisz wartości, które znasz, na rysunku. To ułatwi podstawianie do wzoru.
Sprawdzaj jednostki: Upewnij się, że wszystkie wymiary są podane w tych samych jednostkach. Jeśli nie, zamień je przed obliczeniami. Pamiętaj, że pole wyrażamy w jednostkach kwadratowych (np. cm², m²).
Ćwicz, ćwicz, ćwicz: Rozwiąż jak najwięcej zadań. Im więcej ćwiczysz, tym lepiej zrozumiesz zasady i łatwiej będzie Ci radzić sobie z trudniejszymi zadaniami.
Korzystaj z zasobów: Skorzystaj z podręcznika, zeszytu ćwiczeń, internetu. Poszukaj dodatkowych zadań i przykładów.

Czego unikać?

Unikaj następujących błędów:

Pomylenie wzorów: Upewnij się, że znasz odpowiedni wzór dla każdej figury.
Błędne podstawianie: Sprawdź, czy poprawnie podstawiasz wartości do wzoru.
Zapominanie o jednostkach: Zawsze podawaj jednostki pola (np. cm², m²).
Brak rysunku pomocniczego: Rysunek może znacznie ułatwić rozwiązanie zadania.
Brak sprawdzenia wyniku: Po obliczeniu pola, sprawdź, czy wynik jest realistyczny.

Przykładowe zadanie

Rozważmy następujące zadanie: Oblicz pole trapezu, którego podstawy mają długości 8 cm i 12 cm, a wysokość wynosi 5 cm.

Wzór: Przypomnij sobie wzór na pole trapezu: P = ((a + b) * h) / 2
Podstawianie: Podstawiamy dane do wzoru: P = ((8 cm + 12 cm) * 5 cm) / 2
Obliczenia: Wykonujemy obliczenia: P = (20 cm * 5 cm) / 2 = 100 cm² / 2 = 50 cm²
Odpowiedź: Pole trapezu wynosi 50 cm².

Co jeśli nie rozumiem?

Nie bój się pytać! Jeśli czegoś nie rozumiesz, zapytaj nauczyciela, rodzica, starszego brata lub siostrę, kolegę lub koleżankę z klasy. Możesz również poszukać wyjaśnień w internecie. Istnieje wiele filmów i stron internetowych, które tłumaczą zagadnienia związane z polami figur w prosty i zrozumiały sposób. Pamiętaj, że nie ma głupich pytań!

Alternatywne podejścia

Możesz spotkać się z opiniami, że nauka matematyki, w tym pól figur, jest trudna i nudna. Niektórzy uważają, że lepiej skupić się na innych przedmiotach, które bardziej interesują. Jednak, jak już wspomnieliśmy, wiedza o polach figur jest praktyczna i przydatna w życiu codziennym. Ponadto, rozwiązywanie zadań matematycznych rozwija logiczne myślenie i umiejętność rozwiązywania problemów, co przydaje się w wielu dziedzinach życia.

Podejście rozwiązaniowe

Zamiast skupiać się na trudnościach, spróbuj znaleźć rozwiązania. Podziel materiał na mniejsze części, ucz się stopniowo, rób regularne przerwy. Znajdź sposób, który najlepiej Ci odpowiada. Może to być nauka w grupie, korzystanie z aplikacji edukacyjnych, oglądanie filmów instruktażowych, czy rozwiązywanie zadań online. Pamiętaj, że każdy uczy się w swoim tempie!

Kluczem do sukcesu jest pozytywne nastawienie i wiara we własne możliwości. Pamiętaj, że każdy, nawet najtrudniejszy problem, można rozwiązać, jeśli podejdzie się do niego z odpowiednim nastawieniem i przygotowaniem.

Podsumowanie

Przygotowanie do sprawdzianu z pól figur w klasie 5 wymaga przede wszystkim zrozumienia podstawowych wzorów i regularnej praktyki. Pamiętaj o rysowaniu figur, sprawdzaniu jednostek i unikaniu typowych błędów. Jeśli masz trudności, nie bój się pytać o pomoc. Wykorzystaj dostępne zasoby i znajdź sposób nauki, który najlepiej Ci odpowiada. Pamiętaj, że umiejętność obliczania pól figur przydaje się w wielu sytuacjach życiowych i rozwija logiczne myślenie.

Życzymy Ci powodzenia na sprawdzianie! Dasz radę!

Czy jesteś gotów/gotowa na sprawdzian? Może warto rozwiązać jeszcze kilka zadań na rozgrzewkę?