Sprawdzian Online Z Funkcji Kwadratow 1 Liceum

Sprawdzian Online z Funkcji Kwadratowej dla Liceum (Klasa 1) to, najprościej mówiąc, test sprawdzający Twoją wiedzę na temat funkcji kwadratowych. Nie panikuj! Funkcja kwadratowa to po prostu pewien rodzaj równania, które opisuje parabole, czyli charakterystyczne "uśmiechnięte" lub "smutne" krzywe. Zrozumienie funkcji kwadratowej jest kluczowe w matematyce licealnej i ma zastosowanie w wielu dziedzinach, od fizyki (np. obliczanie toru lotu) po ekonomię (np. modelowanie kosztów).

Ten sprawdzian ma na celu sprawdzenie, czy rozumiesz podstawowe pojęcia związane z funkcją kwadratową, takie jak: postać ogólna, kanoniczna i iloczynowa, współczynniki, miejsca zerowe, wierzchołek paraboli, oś symetrii oraz umiejętność rozwiązywania zadań z ich użyciem.

Krok po kroku: Rozwiązywanie zadań z funkcji kwadratowej

Poniżej znajdziesz uproszczony przewodnik, który pomoże Ci zrozumieć, jak rozwiązywać typowe zadania, jakie mogą pojawić się na sprawdzianie:

1. Rozpoznawanie postaci funkcji kwadratowej

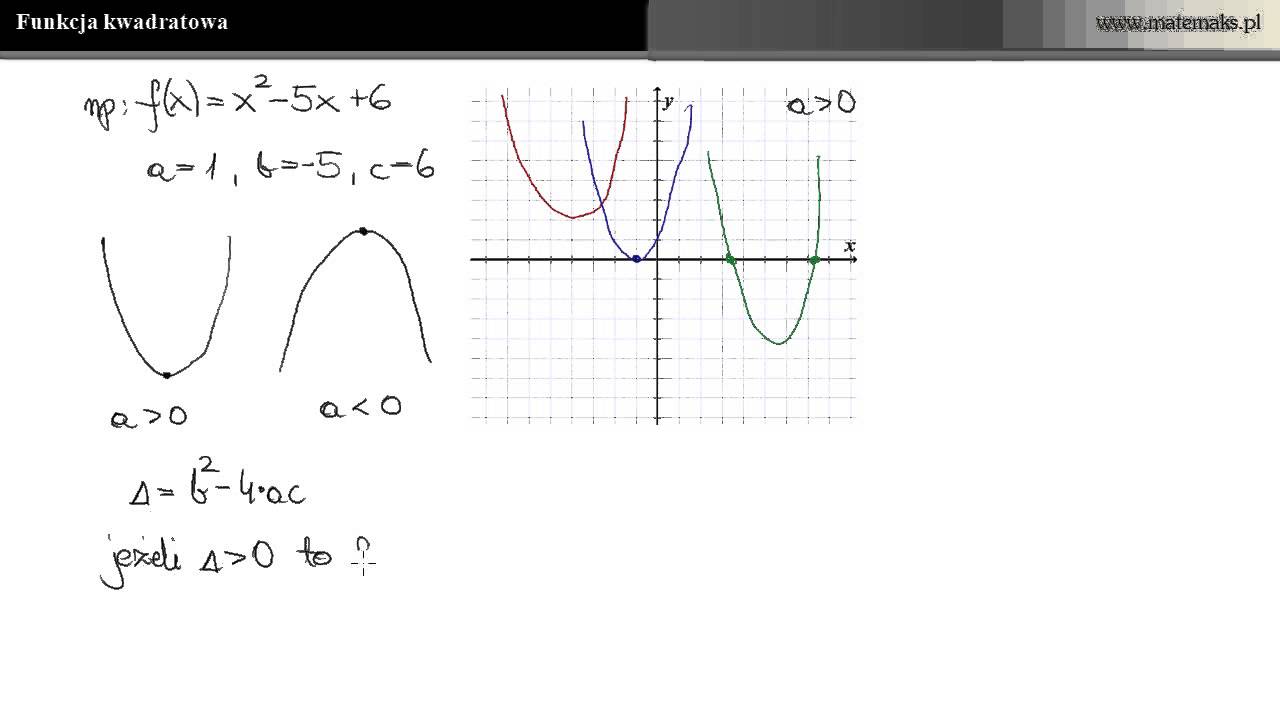
Funkcja kwadratowa może być zapisana w trzech głównych postaciach:

Postać ogólna: f(x) = ax² + bx + c, gdzie a, b, c to współczynniki liczbowe, a a ≠ 0.
Postać kanoniczna: f(x) = a(x - p)² + q, gdzie (p, q) to współrzędne wierzchołka paraboli.
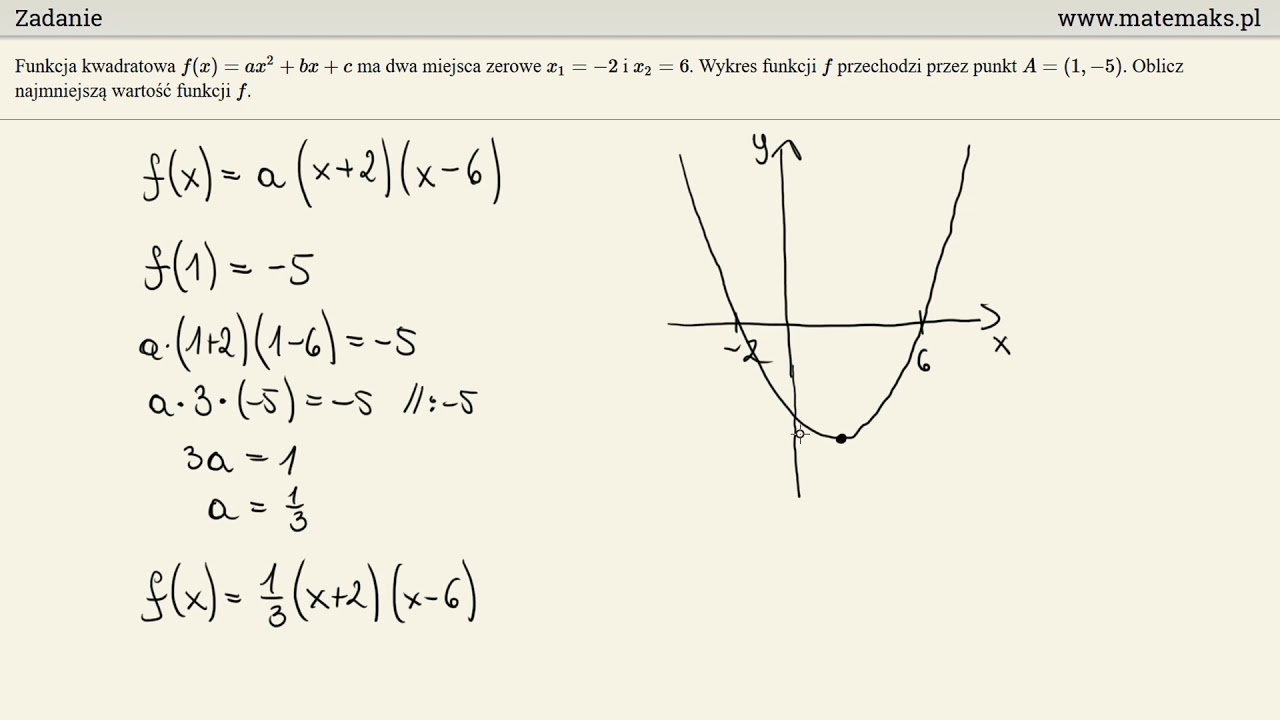
Postać iloczynowa: f(x) = a(x - x₁) (x - x₂), gdzie x₁ i x₂ to miejsca zerowe funkcji.

Przykład: Mamy funkcję f(x) = 2x² + 4x - 6. Jest to postać ogólna. Aby ją zamienić na postać kanoniczną, musimy obliczyć współrzędne wierzchołka (p, q).

2. Obliczanie wierzchołka paraboli

Wierzchołek paraboli to punkt, w którym funkcja osiąga wartość minimalną (dla a > 0) lub maksymalną (dla a < 0). Jego współrzędne obliczamy ze wzorów:

p = -b / 2a
q = -Δ / 4a, gdzie Δ = b² - 4ac (delta)

Przykład: Dla funkcji f(x) = 2x² + 4x - 6:

a = 2, b = 4, c = -6
p = -4 / (2 * 2) = -1
Δ = 4² - 4 * 2 * (-6) = 16 + 48 = 64
q = -64 / (4 * 2) = -8

Zatem wierzchołek paraboli ma współrzędne (-1, -8). Postać kanoniczna to: f(x) = 2(x + 1)² - 8.

3. Obliczanie miejsc zerowych

Miejsca zerowe to punkty, w których funkcja przecina oś x, czyli f(x) = 0. Obliczamy je, rozwiązując równanie kwadratowe:

Obliczamy Δ = b² - 4ac
Jeśli Δ > 0, mamy dwa miejsca zerowe: x₁ = (-b - √Δ) / 2a i x₂ = (-b + √Δ) / 2a
Jeśli Δ = 0, mamy jedno miejsce zerowe: x = -b / 2a
Jeśli Δ < 0, funkcja nie ma miejsc zerowych

Przykład: Dla funkcji f(x) = 2x² + 4x - 6 (wiemy, że Δ = 64):

x₁ = (-4 - √64) / (2 * 2) = (-4 - 8) / 4 = -3
x₂ = (-4 + √64) / (2 * 2) = (-4 + 8) / 4 = 1

Zatem miejsca zerowe to x₁ = -3 i x₂ = 1. Postać iloczynowa to: f(x) = 2(x + 3)(x - 1).

4. Określanie osi symetrii

Oś symetrii to pionowa linia przechodząca przez wierzchołek paraboli. Jej równanie to: x = p, gdzie p to współrzędna x wierzchołka.

Przykład: Dla funkcji f(x) = 2x² + 4x - 6 oś symetrii to x = -1.

5. Rysowanie wykresu

Aby narysować wykres funkcji kwadratowej, potrzebujemy:

Wierzchołek paraboli
Miejsca zerowe (jeśli istnieją)
Kilka dodatkowych punktów (np. dla x = 0, aby znaleźć punkt przecięcia z osią y)

Zaznacz te punkty na układzie współrzędnych i narysuj gładką krzywą przechodzącą przez te punkty, pamiętając o kształcie paraboli.

Praktyczne wskazówki na sprawdzian

Zacznij od prostych zadań. Rozgrzej się, rozwiązując zadania, w których po prostu trzeba zastosować wzór.
Zrozum polecenie. Upewnij się, że dokładnie wiesz, czego dotyczy zadanie. Czy masz znaleźć wierzchołek, miejsca zerowe, czy narysować wykres?
Sprawdzaj obliczenia. Błędy rachunkowe to najczęstsza przyczyna złych odpowiedzi.
Używaj kalkulatora (jeśli jest dozwolony). Ułatwi to obliczenia, szczególnie przy trudniejszych liczbach.
Nie panikuj! Nawet jeśli nie wiesz, jak rozwiązać dane zadanie, spróbuj coś napisać. Często dostaje się punkty za próbę rozwiązania.
Przejrzyj odpowiedzi. Jeśli masz czas, sprawdź wszystkie odpowiedzi, aby upewnić się, że nie popełniłeś żadnych błędów.

Pamiętaj, że praktyka czyni mistrza! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz funkcję kwadratową i tym pewniej będziesz się czuł na sprawdzianie.