Sprawdzian Matematyka Klasa 6 Ulamki Dziesietne

Hej szóstoklasisto! Przed Tobą ważny sprawdzian z ułamków dziesiętnych? Nie martw się! Ten artykuł pomoże Ci się do niego przygotować i zdobyć jak najlepszą ocenę. Skupimy się na najważniejszych zagadnieniach, rozwiążemy przykładowe zadania i damy Ci praktyczne wskazówki.

Czym są Ułamki Dziesiętne?

Ułamki dziesiętne to po prostu sposób zapisu liczb, które są częściami całości. Zapisujemy je za pomocą cyfr i przecinka (w Polsce). To tak, jakbyśmy dzielili pizzę na 10, 100, 1000 kawałków i chcieli zapisać, ile kawałków zjedliśmy!

Przykłady:

0,5 – to połowa (czyli 5/10)
0,25 – to ćwierć (czyli 25/100)
1,75 – to jeden i trzy czwarte (czyli 1 i 75/100)

Pamiętaj! Każda cyfra po przecinku ma swoje znaczenie: pierwsza cyfra to dziesiąte części, druga to setne części, trzecia to tysięczne części i tak dalej.

Działania na Ułamkach Dziesiętnych: Klucz do Sukcesu

Sprawdzian z matematyki najczęściej sprawdza Twoją umiejętność wykonywania działań. Zobaczmy, jak to robić poprawnie:

Dodawanie i Odejmowanie

Najważniejsze to wyrównać przecinki! Napisz liczby jedna pod drugą, tak aby przecinki były w jednej kolumnie. Następnie dodaj lub odejmij tak, jak zwykłe liczby. Przecinek w wyniku będzie w tym samym miejscu, co w dodawanych/odejmowanych liczbach.

Przykład:

2,35 + 1,8 = ?

   2,35
+  1,80  (dopisałem zero, żeby wyrównać ilość cyfr po przecinku)
-------
   4,15

Zatem 2,35 + 1,8 = 4,15

Pamiętaj! Jeśli brakuje cyfr po przecinku, możesz dopisać zera.

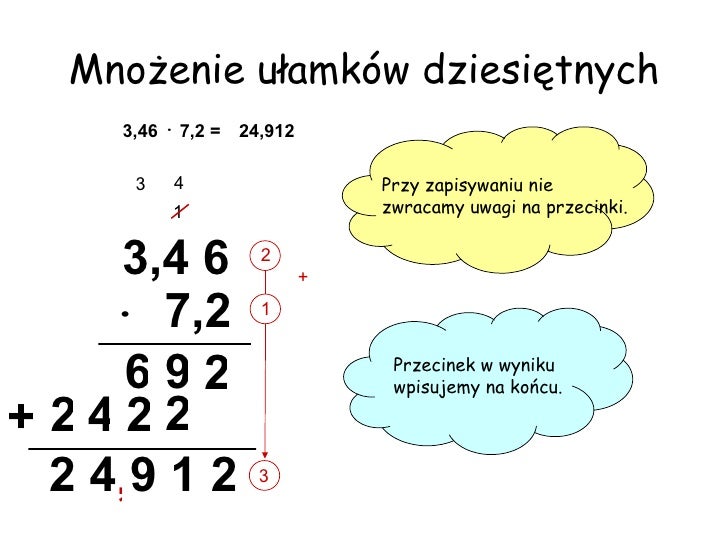
Mnożenie

Mnożymy tak, jakby przecinków nie było! Następnie liczymy, ile łącznie cyfr znajduje się po przecinku w obu mnożonych liczbach. W wyniku przesuwamy przecinek o tyle samo miejsc w lewo.

Przykład:

3,2 x 1,5 = ?

Najpierw mnożymy 32 x 15 = 480

Łącznie w 3,2 i 1,5 mamy 2 cyfry po przecinku (jedna w 3,2 i jedna w 1,5).

Przesuwamy przecinek w 480 o dwa miejsca w lewo: 4,80

Zatem 3,2 x 1,5 = 4,8

Dzielenie

Jeżeli dzielimy ułamek dziesiętny przez liczbę naturalną, dzielimy tak jak zwykłe liczby, a przecinek w wyniku wpisujemy, gdy skończymy dzielenie części całkowitej.

Przykład:

6,4 : 2 = 3,2

Jeżeli dzielimy przez ułamek dziesiętny, musimy przesunąć przecinek w dzielnej i dzielniku o tyle samo miejsc w prawo, aby dzielnik był liczbą naturalną. Potem dzielimy jak zwykle.

Przykład:

1,2 : 0,4 = ?

Przesuwamy przecinki o jedno miejsce w prawo: 12 : 4 = 3

Zatem 1,2 : 0,4 = 3

Zamiana Ułamków Zwykłych na Dziesiętne i Odwrotnie

Czasami trzeba zamienić ułamek zwykły na dziesiętny i odwrotnie. Oto jak to zrobić:

Ułamek Zwykły na Dziesiętny

Najprościej jest rozszerzyć (lub skrócić) ułamek zwykły tak, aby w mianowniku było 10, 100, 1000 itd. Następnie zapisujemy ułamek w postaci dziesiętnej.

Przykład:

1/2 = 5/10 = 0,5

3/4 = 75/100 = 0,75

Jeśli nie da się łatwo rozszerzyć ułamka, możemy podzielić licznik przez mianownik.

Ułamek Dziesiętny na Zwykły

Zapisujemy ułamek dziesiętny jako ułamek zwykły z mianownikiem 10, 100, 1000 itd. w zależności od liczby cyfr po przecinku. Następnie skracamy ułamek, jeśli to możliwe.

Przykład:

0,25 = 25/100 = 1/4

1,5 = 15/10 = 3/2 = 1 1/2

Przykładowe Zadania ze Sprawdzianu (i ich rozwiązania!)

Zobaczmy, jak możemy wykorzystać tę wiedzę w praktyce:

Zadanie: Oblicz: 2,7 + 3,15 = ?
Rozwiązanie: Wyrównujemy przecinki: 2,70 + 3,15 = 5,85
Zadanie: Oblicz: 4,8 - 1,25 = ?
Rozwiązanie: Wyrównujemy przecinki: 4,80 - 1,25 = 3,55
Zadanie: Oblicz: 2,5 x 1,2 = ?
Rozwiązanie: Mnożymy 25 x 12 = 300. Mamy łącznie 2 cyfry po przecinku, więc przesuwamy przecinek o 2 miejsca w lewo: 3,00 = 3
Zadanie: Oblicz: 7,2 : 0,8 = ?
Rozwiązanie: Przesuwamy przecinki o jedno miejsce w prawo: 72 : 8 = 9
Zadanie: Zamień 3/5 na ułamek dziesiętny.
Rozwiązanie: Rozszerzamy ułamek: 3/5 = 6/10 = 0,6

Wskazówki na Sprawdzian

Przed sprawdzianem: Powtórz wszystkie zagadnienia, rozwiąż kilka zadań treningowych.
Podczas sprawdzianu: Czytaj uważnie polecenia, pisz wyraźnie, sprawdzaj swoje obliczenia.
Nie panikuj! Jeśli nie wiesz, jak rozwiązać zadanie, spróbuj je przeanalizować i poszukać podobnych przykładów w zeszycie.

Pamiętaj! Regularna praca i powtarzanie materiału to klucz do sukcesu na sprawdzianie z matematyki. Powodzenia!

Mamy nadzieję, że ten artykuł okazał się pomocny! Teraz jesteś lepiej przygotowany do sprawdzianu z ułamków dziesiętnych. Trzymamy kciuki! Dasz radę!