Sprawdzian Matematyka Klasa 6 Liczby Naturalne I Ułamki

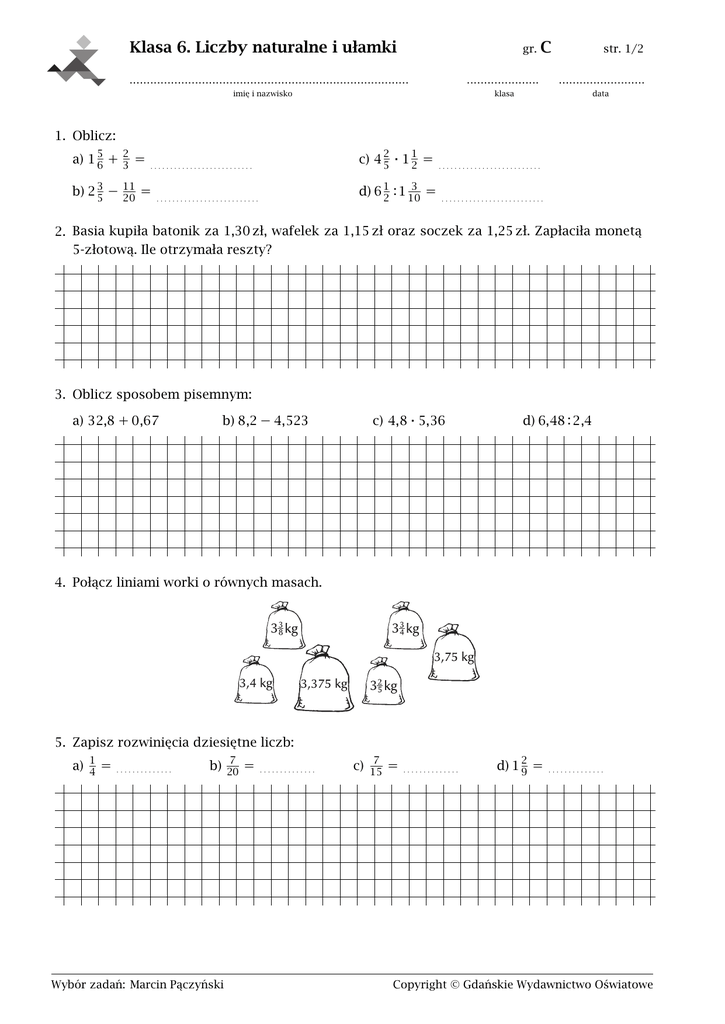
Cześć wszystkim uczniom klasy 6! Widzę, że zbliża się sprawdzian z liczb naturalnych i ułamków. Bez obaw, postaram się wam wszystko wytłumaczyć krok po kroku, żebyście czuli się pewnie i dobrze napisali.

Zacznijmy od podstaw, czyli od liczb naturalnych. Liczby naturalne to po prostu liczby, którymi liczymy, zaczynając od 1. Czyli: 1, 2, 3, 4, 5 i tak dalej, w nieskończoność! Zero nie jest liczbą naturalną.

Działania na liczbach naturalnych

Znamy cztery podstawowe działania: dodawanie, odejmowanie, mnożenie i dzielenie.

Dodawanie: To łączenie liczb. Np. 2 + 3 = 5. Pamiętajcie o pisemnym dodawaniu, jeśli liczby są duże. Ustawiamy liczby jedna pod drugą, tak żeby jedności były pod jednościami, dziesiątki pod dziesiątkami, i tak dalej. Potem dodajemy kolumnami, zaczynając od prawej strony. Jeśli suma w kolumnie jest większa niż 9, przenosimy dziesiątkę do następnej kolumny.
Odejmowanie: To zabieranie jednej liczby od drugiej. Np. 5 - 2 = 3. Podobnie jak przy dodawaniu, przy dużych liczbach odejmujemy pisemnie. Ustawiamy liczby jedna pod drugą (większa na górze), tak samo jak przy dodawaniu. Odejmujemy kolumnami, zaczynając od prawej strony. Jeśli cyfra na górze jest mniejsza niż cyfra na dole, pożyczamy dziesiątkę z następnej kolumny.
Mnożenie: To dodawanie tej samej liczby wiele razy. Np. 3 * 4 = 12 (czyli 3 + 3 + 3 + 3). Mnożenie pisemne wymaga trochę praktyki. Ustawiamy liczby jedna pod drugą. Mnożymy każdą cyfrę dolnej liczby przez każdą cyfrę górnej liczby. Zapisujemy wyniki, przesuwając je za każdym razem o jedno miejsce w lewo. Na koniec dodajemy te wyniki.
Dzielenie: To dzielenie jednej liczby na równe części. Np. 12 / 3 = 4. Dzielenie pisemne, zwane też dzieleniem długim, też wymaga wprawy. Ustawiamy liczby tak, żeby dzielna była wewnątrz "domku", a dzielnik na zewnątrz. Patrzymy, ile razy dzielnik mieści się w pierwszej cyfrze (lub pierwszych cyfrach) dzielnej. Zapisujemy wynik na górze, nad dzielną. Mnożymy ten wynik przez dzielnik i odejmujemy od części dzielnej. Spisujemy następną cyfrę dzielnej i powtarzamy proces.

Kolejność wykonywania działań

Pamiętajcie o kolejności wykonywania działań! Najpierw robimy działania w nawiasach, potem mnożenie i dzielenie (od lewej do prawej), a na końcu dodawanie i odejmowanie (również od lewej do prawej). Zapamiętajcie to sobie jako "Nawiasy, Mnożenie/Dzielenie, Dodawanie/Odejmowanie".

Ułamki

Teraz przejdźmy do ułamków. Ułamek składa się z licznika (liczba na górze) i mianownika (liczba na dole). Mianownik mówi nam, na ile części podzieliliśmy całość, a licznik mówi nam, ile tych części bierzemy. Np. 1/2 (jedna druga) oznacza, że całość podzieliliśmy na dwie równe części i bierzemy jedną z nich.

Rodzaje ułamków

Mamy różne rodzaje ułamków:

Ułamki właściwe: Licznik jest mniejszy od mianownika. Np. 2/5.
Ułamki niewłaściwe: Licznik jest większy lub równy mianownikowi. Np. 5/3 lub 3/3.
Liczby mieszane: Składają się z liczby całkowitej i ułamka właściwego. Np. 1 2/3 (jeden i dwie trzecie).

Zamiana ułamków

Ważne jest, żeby umieć zamieniać ułamki niewłaściwe na liczby mieszane i odwrotnie.

Ułamek niewłaściwy na liczbę mieszaną: Dzielimy licznik przez mianownik. Wynik dzielenia to liczba całkowita, a reszta z dzielenia to licznik ułamka. Mianownik pozostaje bez zmian. Np. 7/3 = 2 1/3 (bo 7 podzielone przez 3 to 2 reszty 1).
Liczba mieszana na ułamek niewłaściwy: Mnożymy liczbę całkowitą przez mianownik, dodajemy licznik i zapisujemy to jako licznik nowego ułamka. Mianownik pozostaje bez zmian. Np. 1 2/5 = 7/5 (bo 1 * 5 + 2 = 7).

Rozszerzanie i skracanie ułamków

Rozszerzanie ułamka to mnożenie licznika i mianownika przez tę samą liczbę. Skracanie ułamka to dzielenie licznika i mianownika przez tę samą liczbę. Oba te działania nie zmieniają wartości ułamka, tylko jego wygląd.

Np. 1/2 rozszerzone przez 2 to 2/4. 4/6 skrócone przez 2 to 2/3.

Skracamy ułamki, żeby doprowadzić je do najprostszej postaci. Szukamy największego wspólnego dzielnika (NWD) licznika i mianownika i dzielimy przez niego obie liczby.

Działania na ułamkach

Dodawanie i odejmowanie ułamków: Możemy dodawać i odejmować tylko ułamki o tych samych mianownikach. Jeśli mianowniki są różne, musimy najpierw sprowadzić ułamki do wspólnego mianownika. Najłatwiej znaleźć najmniejszą wspólną wielokrotność (NWW) mianowników i użyć jej jako wspólny mianownik.

Np. 1/2 + 1/3. NWW dla 2 i 3 to 6. Więc 1/2 = 3/6, a 1/3 = 2/6. Teraz możemy dodać: 3/6 + 2/6 = 5/6.
Mnożenie ułamków: Mnożymy licznik przez licznik, a mianownik przez mianownik. Np. 1/2 * 2/3 = 2/6. Warto sprawdzić, czy przed pomnożeniem można coś skrócić.
Dzielenie ułamków: Dzielenie ułamków to mnożenie przez odwrotność drugiego ułamka. Odwrotność ułamka to zamiana licznika z mianownikiem. Np. odwrotność 2/3 to 3/2.

Np. 1/2 : 2/3 = 1/2 * 3/2 = 3/4.

Porównywanie ułamków

Aby porównać ułamki, najłatwiej sprowadzić je do wspólnego mianownika. Potem porównujemy liczniki. Ułamek z większym licznikiem jest większy.

Np. Czy 2/3 jest większe czy mniejsze od 3/5? Wspólny mianownik to 15. 2/3 = 10/15, a 3/5 = 9/15. Więc 2/3 > 3/5.

Pamiętaj o ćwiczeniach!

Najważniejsze to ćwiczyć, ćwiczyć i jeszcze raz ćwiczyć! Rozwiązuj zadania z podręcznika, zeszytu ćwiczeń, a także znajdź dodatkowe zadania w Internecie. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz te zagadnienia i tym pewniej będziesz się czuł na sprawdzianie.

Przykładowe zadania

Oblicz: (12 + 8) * 3 – 5 * 4
Oblicz pisemnie: 345 + 678, 987 – 234, 45 * 23, 765 : 5
Zamień ułamek niewłaściwy na liczbę mieszaną: 11/4
Zamień liczbę mieszaną na ułamek niewłaściwy: 2 1/3
Skróć ułamek: 12/18
Rozszerz ułamek: 2/5 przez 3
Oblicz: 1/4 + 2/4, 3/5 – 1/5, 1/2 + 1/3, 2/3 – 1/4, 1/2 * 3/4, 2/5 : 1/2
Porównaj ułamki: 1/3 i 2/5

Spróbuj rozwiązać te zadania. Jeśli masz z czymś problem, wróć do wyjaśnień powyżej lub poproś o pomoc nauczyciela albo kogoś z rodziny.

Co jeszcze warto powtórzyć?

Dzielniki i wielokrotności: Warto przypomnieć sobie, co to są dzielniki i wielokrotności liczb. Dzielnik to liczba, przez którą można podzielić daną liczbę bez reszty. Wielokrotność to liczba, która jest wynikiem pomnożenia danej liczby przez inną liczbę naturalną.
Cechy podzielności: Znajomość cech podzielności przez 2, 3, 4, 5, 9 i 10 bardzo ułatwia dzielenie i skracanie ułamków.
Zadania tekstowe: Na sprawdzianie mogą pojawić się zadania tekstowe, które wymagają zastosowania wiedzy o liczbach naturalnych i ułamkach w praktyce. Czytaj uważnie treść zadania, wypisz dane i zastanów się, jakie działania musisz wykonać, żeby rozwiązać zadanie.

Wskazówki na sprawdzian

Przeczytaj uważnie wszystkie zadania.
Zacznij od zadań, które wydają Ci się najłatwiejsze.
Nie spędzaj zbyt dużo czasu nad jednym zadaniem. Jeśli nie wiesz, jak je rozwiązać, przejdź do następnego i wróć do niego później.
Sprawdź swoje odpowiedzi. Upewnij się, że nie popełniłeś żadnych błędów rachunkowych.
Pisz czytelnie. Nauczyciel musi móc przeczytać Twoje odpowiedzi.
Bądź pewny siebie! Wierzę w Ciebie!

Pamiętajcie, matematyka wcale nie musi być straszna! Wystarczy trochę wysiłku i systematycznej pracy. Trzymam za Was kciuki i życzę powodzenia na sprawdzianie!

Dodatkowe materiały

Jeśli potrzebujecie więcej materiałów do nauki, poszukajcie w Internecie. Jest mnóstwo stron internetowych i filmów edukacyjnych, które mogą Wam pomóc w zrozumieniu liczb naturalnych i ułamków. Możecie też poprosić nauczyciela o dodatkowe zadania lub wyjaśnienia.

Życzę Wam owocnej nauki i wspaniałych wyników! Pamiętajcie, że najważniejsze to się nie poddawać i wierzyć w siebie!