Sprawdzian Klasa 7 Ulamki Zwykle I Dziesietne

Czy zbliża się sprawdzian z ułamków w klasie 7? Stresujesz się? Spokojnie! Ten artykuł jest dla Ciebie. Przygotowaliśmy kompleksowy przewodnik, który pomoże Ci opanować ułamki zwykłe i dziesiętne, zrozumieć ich zastosowanie i przede wszystkim – napisać sprawdzian na szóstkę! Skupimy się na praktycznych przykładach i wyjaśnieniach, aby matematyka przestała być straszna, a stała się zrozumiała.

Co Cię Czeka na Sprawdzianie?

Sprawdziany z ułamków w klasie 7 zwykle obejmują następujące zagadnienia:

Zamiana ułamków zwykłych na dziesiętne i odwrotnie: Czy wiesz, jak zapisać ¹/₄ jako 0,25 i odwrotnie?
Porównywanie ułamków: Który ułamek jest większy: ²/₅ czy ³/₇?
Działania na ułamkach zwykłych: Dodawanie, odejmowanie, mnożenie i dzielenie ułamków.
Działania na ułamkach dziesiętnych: Dodawanie, odejmowanie, mnożenie i dzielenie ułamków dziesiętnych.
Ułamki jako część całości: Zadania tekstowe wykorzystujące ułamki do opisywania części jakiejś wielkości.
Zaokrąglanie ułamków dziesiętnych: Umiejętność zaokrąglania do określonego miejsca po przecinku.
Ułamki w kontekście praktycznym: Rozwiązywanie problemów z życia codziennego, w których występują ułamki.

Zrozumienie tych punktów jest kluczowe do sukcesu na sprawdzianie. Pokażemy Ci, jak to zrobić krok po kroku!

Zamiana Ułamków Zwykłych na Dziesiętne i Odwrotnie

Z Ułamka Zwykłego na Dziesiętny

Najprostszy sposób to podzielić licznik przez mianownik. Na przykład:

¹/₂ = 1 : 2 = 0,5
³/₄ = 3 : 4 = 0,75

Czasami ułamek ma w mianowniku 10, 100, 1000… Wtedy zamiana jest jeszcze prostsza:

⁷/₁₀ = 0,7
²³/₁₀₀ = 0,23
¹⁵⁹/₁₀₀₀ = 0,159

Jeśli mianownik nie jest potęgą dziesiątki, spróbuj go do niej sprowadzić (jeśli to możliwe). Na przykład, ¹/₅ można pomnożyć licznik i mianownik przez 2, otrzymując ²/₁₀ = 0,2.

Z Ułamka Dziesiętnego na Zwykły

Zapisujemy ułamek dziesiętny jako ułamek, w którym licznik to liczba bez przecinka, a mianownik to 10, 100, 1000… w zależności od liczby miejsc po przecinku. Następnie upraszczamy ułamek, dzieląc licznik i mianownik przez ich największy wspólny dzielnik.

0,5 = ⁵/₁₀ = ¹/₂
0,25 = ²⁵/₁₀₀ = ¹/₄
0,125 = ¹²⁵/₁₀₀₀ = ¹/₈

Pamiętaj o upraszczaniu ułamków! Nauczyciele często wymagają, aby wynik był podany w najprostszej postaci.

Porównywanie Ułamków

Porównywanie ułamków może być proste lub trochę trudniejsze, w zależności od sytuacji.

Ułamki o Tym Samym Mianowniku

Jeśli ułamki mają ten sam mianownik, większy jest ten, który ma większy licznik. Na przykład:

³/₇ > ²/₇ (bo 3 > 2)
⁵/₁₁ < ⁸/₁₁ (bo 5 < 8)

Ułamki o Różnych Mianownikach

Jeśli ułamki mają różne mianowniki, musimy sprowadzić je do wspólnego mianownika. Najczęściej szukamy najmniejszej wspólnej wielokrotności (NWW) mianowników.

Przykład: Porównaj ²/₅ i ³/₇.

NWW(5, 7) = 35
²/₅ = ^{(2 * 7)}/_{(5 * 7)} = ¹⁴/₃₅
³/₇ = ^{(3 * 5)}/_{(7 * 5)} = ¹⁵/₃₅
Ponieważ ¹⁵/₃₅ > ¹⁴/₃₅, to ³/₇ > ²/₅.

Można też zamienić ułamki na dziesiętne i porównać liczby po przecinku.

Działania na Ułamkach Zwykłych

Dodawanie i Odejmowanie

Podobnie jak przy porównywaniu, musimy sprowadzić ułamki do wspólnego mianownika. Następnie dodajemy lub odejmujemy liczniki, a mianownik pozostaje bez zmian.

Przykłady:

¹/₄ + ²/₄ = ³/₄
⁵/₆ - ¹/₆ = ⁴/₆ = ²/₃ (pamiętaj o uproszczeniu!)

Jeśli mianowniki są różne:

¹/₃ + ¹/₄ = ^{(1 * 4)}/_{(3 * 4)} + ^{(1 * 3)}/_{(4 * 3)} = ⁴/₁₂ + ³/₁₂ = ⁷/₁₂

Mnożenie

Mnożenie ułamków jest proste: mnożymy licznik przez licznik, a mianownik przez mianownik.

Przykłady:

¹/₂ * ²/₃ = ^{(1 * 2)}/_{(2 * 3)} = ²/₆ = ¹/₃
³/₅ * ¹/₄ = ^{(3 * 1)}/_{(5 * 4)} = ³/₂₀

Często można skrócić ułamki przed mnożeniem, co ułatwia obliczenia. Spójrz na przykład pierwszy: ¹/₂ * ²/₃. Można skrócić 2 w liczniku i mianowniku, co daje od razu ¹/₃.

Dzielenie

Dzielenie ułamków polega na pomnożeniu pierwszego ułamka przez odwrotność drugiego. Odwrotność ułamka to zamiana licznika z mianownikiem.

Przykłady:

¹/₂ : ¹/₃ = ¹/₂ * ³/₁ = ³/₂ = 1¹/₂
²/₅ : ³/₄ = ²/₅ * ⁴/₃ = ⁸/₁₅

Pamiętaj, że dzielenie to mnożenie przez odwrotność!

Działania na Ułamkach Dziesiętnych

Działania na ułamkach dziesiętnych przypominają działania na liczbach całkowitych, ale trzeba uważać na przecinek.

Dodawanie i Odejmowanie

Ustaw ułamki tak, aby przecinek był pod przecinkiem. Dodaj lub odejmij cyfry w kolumnach, zaczynając od prawej strony. Przecinek w wyniku będzie w tym samym miejscu, co w dodawanych/odejmowanych ułamkach.

Przykłady:

2,5 + 1,3 = 3,8
4,7 - 2,1 = 2,6
3,15 + 1,8 = 4,95 (pamiętaj o dopisaniu zera, aby wyrównać liczbę miejsc po przecinku)

Mnożenie

Mnożymy ułamki dziesiętne jak liczby całkowite, ignorując przecinek na początku. Następnie w wyniku oddzielamy tyle miejsc po przecinku, ile łącznie jest w mnożonych liczbach.

Przykłady:

2,5 * 1,2 = 3,00 (25 * 12 = 300, łącznie dwa miejsca po przecinku w 2,5 i 1,2, więc wynik to 3,00 = 3)
0,3 * 0,4 = 0,12 (3 * 4 = 12, łącznie dwa miejsca po przecinku w 0,3 i 0,4, więc wynik to 0,12)

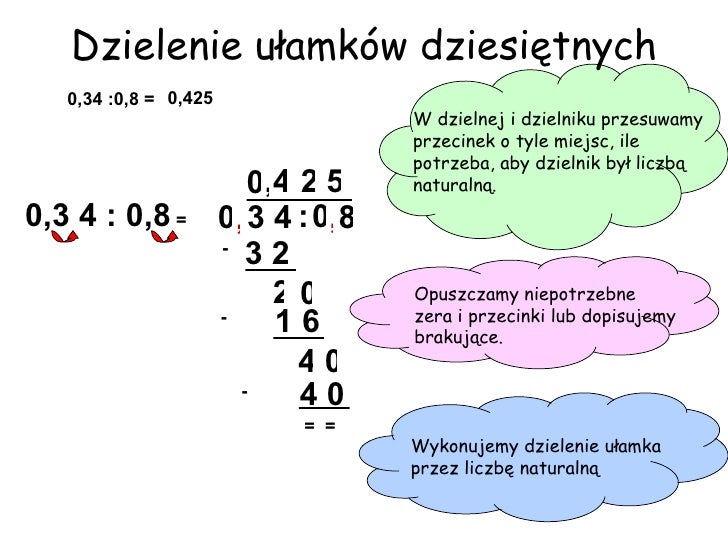
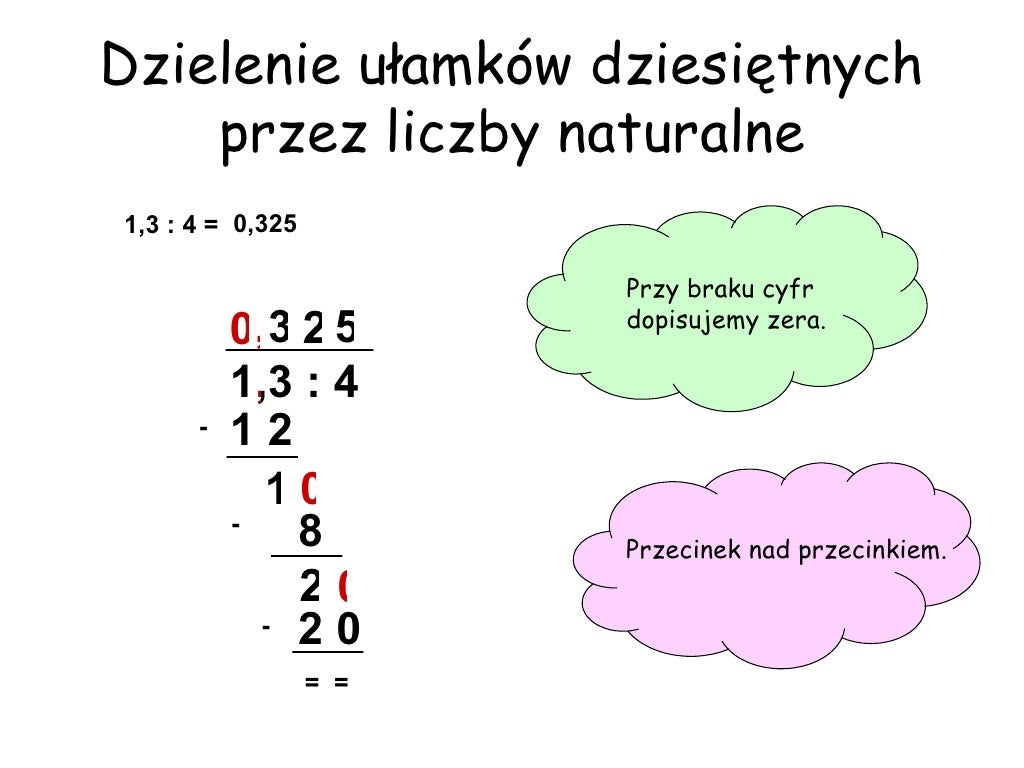
Dzielenie

Dzielenie ułamków dziesiętnych jest trochę bardziej skomplikowane. Jeśli dzielnik jest liczbą dziesiętną, musimy przesunąć przecinek w dzielniku i dzielnej o tyle samo miejsc w prawo, aby dzielnik stał się liczbą całkowitą. Następnie dzielimy jak zwykłe liczby.

Przykład: 4,8 : 1,2

Przesuwamy przecinek w 4,8 i 1,2 o jedno miejsce w prawo, otrzymując 48 : 12.
48 : 12 = 4

Przykład: 3,6 : 0,09

Przesuwamy przecinek w 3,6 i 0,09 o dwa miejsca w prawo, otrzymując 360 : 9.
360 : 9 = 40

Ułamki jako Część Całości

Wiele zadań tekstowych dotyczy ułamków jako części całości. W takich zadaniach musimy zrozumieć, co reprezentuje ułamek i jak go użyć do obliczenia pewnej wielkości.

Przykład: W klasie jest 30 uczniów. ²/₅ to dziewczęta. Ile jest dziewcząt w klasie?

Rozwiązanie: Obliczamy ²/₅ z 30, czyli (²/₅) * 30 = (2 * 30) / 5 = 60 / 5 = 12. W klasie jest 12 dziewcząt.

Przykład: Książka ma 200 stron. Janek przeczytał ³/₄ książki. Ile stron mu zostało do przeczytania?

Obliczamy ile stron Janek przeczytał: (³/₄) * 200 = 150
Odejmujemy przeczytane strony od całkowitej liczby stron: 200 - 150 = 50
Janek ma do przeczytania 50 stron.

Zaokrąglanie Ułamków Dziesiętnych

Zaokrąglanie ułamków dziesiętnych polega na przybliżeniu liczby do określonej dokładności. Zwykle zaokrąglamy do pełnych jednostek, dziesiątek, setnych, itp.

Zasady zaokrąglania:

Jeśli cyfra, która następuje po cyfrze, do której zaokrąglamy, jest mniejsza niż 5, to cyfrę, do której zaokrąglamy, zostawiamy bez zmian.
Jeśli cyfra, która następuje po cyfrze, do której zaokrąglamy, jest większa lub równa 5, to cyfrę, do której zaokrąglamy, zwiększamy o 1.

Przykłady:

3,1415 zaokrąglone do dwóch miejsc po przecinku to 3,14.
3,1415 zaokrąglone do jednego miejsca po przecinku to 3,1.
3,1415 zaokrąglone do pełnej liczby to 3.
4,789 zaokrąglone do dwóch miejsc po przecinku to 4,79.
4,789 zaokrąglone do jednego miejsca po przecinku to 4,8.

Ułamki w Kontekście Praktycznym

Ułamki są wszędzie! W przepisach kulinarnych, podczas mierzenia, obliczania rabatów w sklepie… Umiejętność operowania ułamkami przydaje się w życiu codziennym.

Przykłady:

Gotowanie: Przepis wymaga ¹/₂ szklanki mąki. Masz tylko ¹/₄ szklanki. Ile jeszcze musisz dodać?
Zakupy: Bluza kosztuje 80 zł. Jest przeceniona o 20%. Ile zapłacisz za bluzę? (20% to ¹/₅)
Mierzenie: Masz deskę o długości 1,5 metra. Musisz ją podzielić na 3 równe części. Jak długa będzie każda część?
Podróże: Przejechałeś ²/₃ trasy. Zostało Ci 100 km. Jaka jest długość całej trasy?

Podsumowanie i Wskazówki

Ułamki mogą wydawać się trudne, ale z odpowiednim podejściem i praktyką stają się zrozumiałe i łatwe. Kluczem do sukcesu jest:

Zrozumienie definicji ułamka i jego związku z całością.
Ćwiczenie zamiany ułamków zwykłych na dziesiętne i odwrotnie.
Opanowanie działań na ułamkach.
Rozwiązywanie zadań tekstowych, aby zobaczyć, jak ułamki działają w praktyce.
Nie bój się pytać! Jeśli czegoś nie rozumiesz, zapytaj nauczyciela, kolegę lub poszukaj informacji w internecie.

Pamiętaj, matematyka to umiejętność, którą można wyćwiczyć. Im więcej ćwiczysz, tym lepiej będziesz radzić sobie z ułamkami i innymi zagadnieniami matematycznymi. Powodzenia na sprawdzianie! Wierzymy w Ciebie!