Sprawdzian Klasa 5 Ułamki Zwykłe

Zbliża się sprawdzian z ułamków zwykłych w 5 klasie? Wiem, jak bardzo stresujące może być to dla Ciebie. Ułamki, choć wydają się proste, potrafią przysporzyć sporo trudności. Pamiętaj, że nie jesteś sam! Wielu uczniów ma podobne obawy. Spróbujmy wspólnie przez to przejść.

Dlaczego ułamki zwykłe są takie ważne?

Możesz się zastanawiać, po co w ogóle uczymy się o ułamkach zwykłych. Czy to tylko teoria, która nie ma zastosowania w życiu? Nic bardziej mylnego! Ułamki są wszędzie wokół nas:

• Przepisy kulinarne: Potrzebujesz połowę szklanki mąki? To ułamek!
• Podział pizzy: Kto dostanie 1/4 pizzy? Kolejny ułamek!
• Mierzenie czasu: Pół godziny, kwadrans – znowu ułamki!
• Zakupy: Połowa ceny? Rabat 1/3? Ułamki pomagają oszczędzać!

Zrozumienie ułamków pozwala lepiej radzić sobie w codziennych sytuacjach i rozwija umiejętność logicznego myślenia. To podstawa do dalszej nauki matematyki, w tym ułamków dziesiętnych i procentów.

Najczęstsze problemy z ułamkami zwykłymi

Zanim przejdziemy do rozwiązań, warto zidentyfikować, co sprawia Ci najwięcej trudności. Do najczęstszych problemów należą:

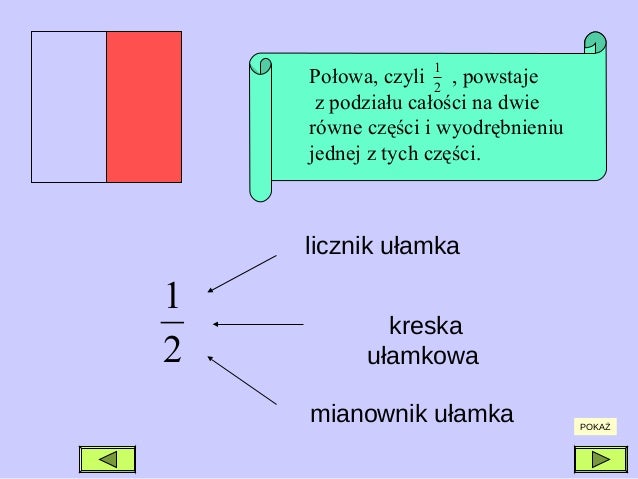
• Rozumienie definicji: Co to jest licznik, a co mianownik? Jak je zapamiętać?
• Sprowadzanie do wspólnego mianownika: Skąd się biorą te liczby? Dlaczego to robimy?
• Dodawanie i odejmowanie: Kiedy mogę dodawać/odejmować ułamki bezpośrednio?
• Mnożenie i dzielenie: Co się dzieje z licznikiem i mianownikiem?
• Upraszczanie ułamków: Jak znaleźć największy wspólny dzielnik?
• Porównywanie ułamków: Który ułamek jest większy?
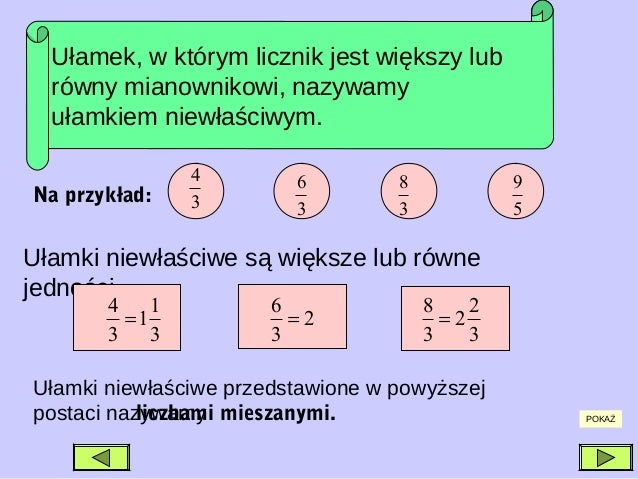
• Zamiana ułamków niewłaściwych na liczby mieszane: Co to w ogóle jest liczba mieszana?

Wiele osób uważa, że ułamki to tylko wzory do zapamiętania. To prawda, wzory są ważne, ale ważniejsze jest zrozumienie, co się za nimi kryje. Wtedy łatwiej je zapamiętać i zastosować w praktyce.

Jak przygotować się do sprawdzianu z ułamków zwykłych?

Oto kilka sprawdzonych metod, które pomogą Ci dobrze przygotować się do sprawdzianu:

1. Zrozumienie podstawowych pojęć

Upewnij się, że rozumiesz, co oznaczają następujące pojęcia:

• Licznik: Mówi, ile części całości bierzemy.
• Mianownik: Mówi, na ile części dzielimy całość.
• Ułamek właściwy: Licznik jest mniejszy od mianownika (np. 1/2, 3/4).
• Ułamek niewłaściwy: Licznik jest większy lub równy mianownikowi (np. 5/3, 7/7).
• Liczba mieszana: Składa się z liczby całkowitej i ułamka właściwego (np. 1 1/2, 2 3/4).

Pamiętaj o wizualizacji! Wyobraź sobie pizzę podzieloną na kawałki. Licznik to liczba kawałków, które zjadasz, a mianownik to liczba wszystkich kawałków.

2. Sprowadzanie do wspólnego mianownika

To kluczowa umiejętność przy dodawaniu i odejmowaniu ułamków. Co to znaczy "wspólny mianownik"? To mianownik, który jest wielokrotnością obu (lub więcej) mianowników ułamków, które chcemy dodać lub odjąć. Najprościej jest znaleźć najmniejszą wspólną wielokrotność (NWW) mianowników.

Przykład: Chcemy dodać 1/2 + 1/3. NWW liczb 2 i 3 to 6. Musimy więc sprowadzić oba ułamki do mianownika 6:

• 1/2 = 3/6 (bo 1 * 3 = 3, 2 * 3 = 6)
• 1/3 = 2/6 (bo 1 * 2 = 2, 3 * 2 = 6)

Teraz możemy dodać: 3/6 + 2/6 = 5/6.

3. Dodawanie i odejmowanie ułamków

Jeśli ułamki mają wspólny mianownik, wystarczy dodać (lub odjąć) liczniki, a mianownik pozostawić bez zmian.

Przykład: 2/5 + 1/5 = 3/5

Jeśli ułamki nie mają wspólnego mianownika, musimy je najpierw sprowadzić do wspólnego mianownika, a następnie dodać lub odjąć liczniki.

4. Mnożenie i dzielenie ułamków

Mnożenie ułamków jest proste: mnożymy licznik przez licznik i mianownik przez mianownik.

Przykład: 1/2 * 2/3 = (1 * 2) / (2 * 3) = 2/6 = 1/3 (po uproszczeniu)

Dzielenie ułamków to mnożenie przez odwrotność drugiego ułamka. Odwrotność ułamka to zamiana licznika z mianownikiem.

Przykład: 1/2 : 2/3 = 1/2 * 3/2 = (1 * 3) / (2 * 2) = 3/4

5. Upraszczanie ułamków

Upraszczanie ułamków polega na podzieleniu licznika i mianownika przez ten sam dzielnik. Chcemy znaleźć jak największy dzielnik, aby otrzymać ułamek w najprostszej postaci.

Przykład: 4/8 można uprościć, dzieląc licznik i mianownik przez 4. 4/8 = 1/2.

Upraszczaj ułamki zawsze, gdy to możliwe! To ułatwi dalsze obliczenia i zmniejszy ryzyko pomyłki.

6. Zamiana ułamków niewłaściwych na liczby mieszane i odwrotnie

Ułamek niewłaściwy (np. 5/3) możemy zamienić na liczbę mieszaną (1 2/3) poprzez podzielenie licznika przez mianownik. Wynik dzielenia to liczba całkowita, a reszta to licznik ułamka właściwego.

Przykład: 5/3 = 1 reszty 2, więc 5/3 = 1 2/3.

Aby zamienić liczbę mieszaną na ułamek niewłaściwy, mnożymy liczbę całkowitą przez mianownik ułamka i dodajemy do licznika. Mianownik pozostaje bez zmian.

Przykład: 1 2/3 = (1 * 3 + 2) / 3 = 5/3.

7. Ćwiczenia, ćwiczenia i jeszcze raz ćwiczenia!

Najlepszym sposobem na opanowanie ułamków jest rozwiązywanie zadań. Im więcej zadań zrobisz, tym lepiej zrozumiesz zasady i unikniesz błędów na sprawdzianie. Skorzystaj z podręcznika, zeszytu ćwiczeń, a także z zasobów internetowych. Poproś nauczyciela o dodatkowe zadania, jeśli czujesz, że potrzebujesz więcej praktyki.

8. Praca z błędem

Nie zrażaj się, jeśli popełniasz błędy! Analizuj swoje błędy i staraj się zrozumieć, dlaczego je popełniłeś. To najlepszy sposób na naukę. Zapisz sobie, jakie błędy najczęściej popełniasz, i skup się na tych zagadnieniach. Możesz poprosić kolegę lub nauczyciela o pomoc w zrozumieniu błędów.

9. Odpoczynek i relaks

Pamiętaj o regularnych przerwach podczas nauki. Wychodź na spacer, posłuchaj muzyki, zrób coś, co lubisz. Przemęczony mózg nie przyswaja wiedzy. Dzień przed sprawdzianem zrelaksuj się i dobrze wyśpij. Stres może pogorszyć Twoje wyniki.

Kontrargumenty: "Ułamki są nudne i trudne!"

To prawda, że dla niektórych ułamki mogą wydawać się nudne i trudne. Ale spróbuj spojrzeć na nie z innej strony. Potraktuj je jako łamigłówki do rozwiązania. Każde zadanie to wyzwanie, a rozwiązanie to satysfakcja. Zauważ, że rozumienie ułamków otwiera drzwi do bardziej zaawansowanej matematyki i pozwala lepiej zrozumieć świat wokół nas. A trudności? Każdy z nas je ma! Nie poddawaj się, proś o pomoc i ćwicz, a zobaczysz, że ułamki staną się dla Ciebie coraz łatwiejsze.

Przykładowe zadania na sprawdzian z ułamków zwykłych

Oto kilka przykładów zadań, które mogą pojawić się na sprawdzianie:

• Sprowadź ułamki 2/3 i 1/4 do wspólnego mianownika.
• Oblicz: 1/2 + 1/3 - 1/6.
• Oblicz: 2/5 * 3/4.
• Oblicz: 1/3 : 2/5.
• Uprość ułamek 12/18.
• Zamień ułamek niewłaściwy 7/3 na liczbę mieszaną.
• Zamień liczbę mieszaną 2 1/4 na ułamek niewłaściwy.
• Który ułamek jest większy: 3/5 czy 2/3?
• Mama upiekła ciasto i podzieliła je na 12 kawałków. Tomek zjadł 3 kawałki, a Kasia 4 kawałki. Jaką część ciasta zjedli Tomek i Kasia razem?

Rozwiązując te zadania, upewnij się, że rozumiesz każdy krok i potrafisz go wytłumaczyć. To pomoże Ci utrwalić wiedzę i zwiększyć pewność siebie przed sprawdzianem.

Pamiętaj!

• Bądź systematyczny w nauce. Nie zostawiaj wszystkiego na ostatnią chwilę.
• Nie bój się pytać. Jeśli czegoś nie rozumiesz, zapytaj nauczyciela, rodzica lub kolegę.
• Wierz w siebie. Jesteś w stanie nauczyć się ułamków zwykłych!

Powodzenia na sprawdzianie! Pamiętaj, że wynik sprawdzianu nie definiuje Ciebie jako osoby. Liczy się to, ile pracy włożyłeś w naukę i ile się nauczyłeś.

Jak czujesz się teraz, po przeczytaniu tego artykułu? Czy wiesz, od czego zaczniesz przygotowania do sprawdzianu?