Sprawdzian Klasa 5 Pola Figur

Czy Twój uczeń klasy 5 zbliża się do sprawdzianu z pól figur i czujesz, że zaczyna się stresować? To absolutnie normalne! Geometria, a w szczególności obliczanie pól, potrafi sprawić trudność, zwłaszcza na tak wczesnym etapie edukacji. Pamiętaj, że kluczem do sukcesu jest zrozumienie, a nie tylko zapamiętywanie wzorów.
Ten artykuł powstał, aby pomóc uczniom klasy 5 opanować zagadnienia związane z polami figur i podejść do sprawdzianu z pewnością siebie. Znajdziesz tutaj praktyczne wskazówki, przykłady i proste wyjaśnienia, które pomogą zrozumieć podstawy geometrii.
Zrozumienie Podstaw: Czym Jest Pole?
Zanim przejdziemy do konkretnych figur, ważne jest, aby zrozumieć, czym w ogóle jest pole. Wyobraź sobie, że malujesz pokój. Pole to ilość farby, której potrzebujesz, aby pokryć całą podłogę. Inaczej mówiąc, pole to miara powierzchni, jaką zajmuje dana figura.
Pole mierzymy w jednostkach kwadratowych, takich jak centymetry kwadratowe (cm²) lub metry kwadratowe (m²). To ważne, żeby o tym pamiętać, podając wynik!
Pola Podstawowych Figur: Prostokąt i Kwadrat
Zaczynamy od figur, które uczniowie poznają jako pierwsze. Prostokąt i kwadrat to fundament geometrii!
Prostokąt: Długość razy Szerokość
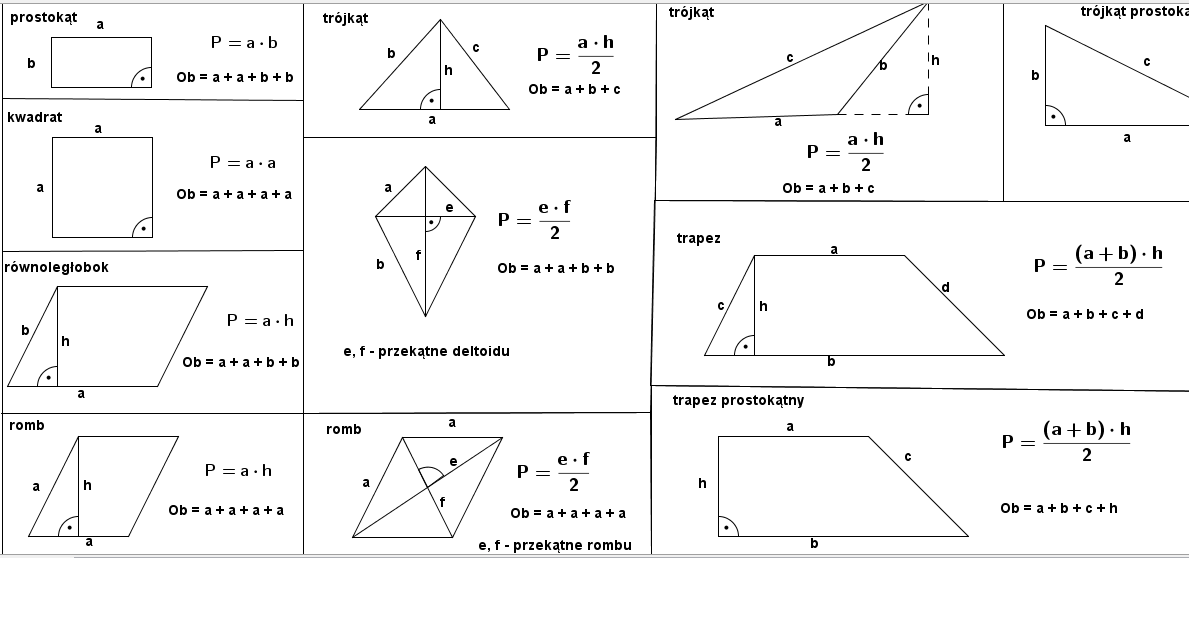
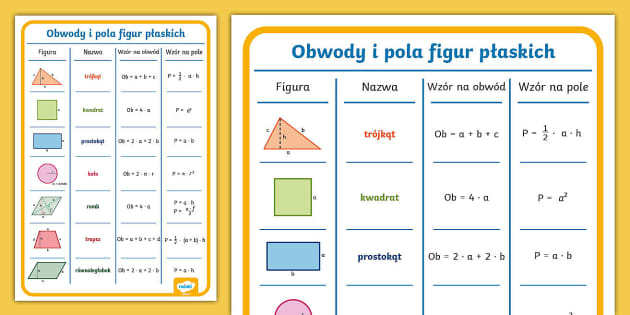
Pole prostokąta obliczamy, mnożąc jego długość (a) przez szerokość (b). Czyli:
Pole prostokąta = a * b
Przykład: Prostokąt ma długość 5 cm i szerokość 3 cm. Jego pole wynosi 5 cm * 3 cm = 15 cm².
Praktyczna wskazówka: Zawsze upewnij się, że długość i szerokość są podane w tej samej jednostce! Jeśli jedna jest w centymetrach, a druga w metrach, najpierw trzeba je zamienić.
Kwadrat: Bok razy Bok
Kwadrat to szczególny rodzaj prostokąta, w którym wszystkie boki są równe. Dlatego pole kwadratu obliczamy, mnożąc długość jego boku (a) przez samą siebie. Czyli:
Pole kwadratu = a * a = a²
Przykład: Kwadrat ma bok o długości 4 cm. Jego pole wynosi 4 cm * 4 cm = 16 cm².
Praktyczna wskazówka: Zapamiętaj, że kwadrat ma wszystkie boki równe. To znacznie ułatwia obliczenia!
Pole Trójkąta: Połowa Podstawy Razy Wysokość
Obliczanie pola trójkąta to kolejny ważny element. Tutaj wkracza pojęcie wysokości, czyli odcinka prostopadłego do podstawy i łączącego ją z wierzchołkiem trójkąta.
Pole trójkąta = (podstawa * wysokość) / 2 = (a * h) / 2
Gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę.
Przykład: Trójkąt ma podstawę o długości 6 cm i wysokość opuszczoną na tę podstawę o długości 4 cm. Jego pole wynosi (6 cm * 4 cm) / 2 = 12 cm².
Praktyczna wskazówka: Czasem wysokość trójkąta może leżeć poza jego obrysem! Nie daj się tym zmylić. Ważne, żeby była prostopadła do podstawy.
Pole Równoległoboku: Podstawa Razy Wysokość
Równoległobok to figura, która na pierwszy rzut oka może wydawać się trudna, ale zasada obliczania pola jest prosta, podobna do prostokąta.
Pole równoległoboku = podstawa * wysokość = a * h
Gdzie a to długość podstawy, a h to wysokość opuszczona na tę podstawę.
Przykład: Równoległobok ma podstawę o długości 8 cm i wysokość opuszczoną na tę podstawę o długości 5 cm. Jego pole wynosi 8 cm * 5 cm = 40 cm².
Praktyczna wskazówka: Zauważ, że wysokość równoległoboku to odległość między podstawą a bokiem do niej równoległym. Nie myl jej z długością boku!
Pole Rombu: Dwa Sposoby
Romb, czyli równoległobok, który ma wszystkie boki równe, można obliczyć na dwa sposoby.
Sposób 1: Podstawa Razy Wysokość
Tak jak w przypadku równoległoboku:
Pole rombu = podstawa * wysokość = a * h
Sposób 2: Połowa Iloczynu Przekątnych
Romb ma dwie przekątne (d1 i d2), które przecinają się pod kątem prostym. Wzór na pole rombu wykorzystujący przekątne to:
Pole rombu = (d1 * d2) / 2
Przykład: Romb ma przekątne o długości 6 cm i 8 cm. Jego pole wynosi (6 cm * 8 cm) / 2 = 24 cm².
Praktyczna wskazówka: Wybierz sposób obliczania pola rombu, który jest najłatwiejszy w danej sytuacji. Jeśli znasz podstawę i wysokość, użyj pierwszego wzoru. Jeśli znasz przekątne, użyj drugiego.
Pole Trapezu: Średnia Długość Podstaw Razy Wysokość
Trapez to czworokąt, który ma co najmniej jedną parę boków równoległych (podstaw). Obliczanie jego pola wymaga znajomości długości obu podstaw (a i b) oraz wysokości (h).
Pole trapezu = ((a + b) / 2) * h
Czyli dodajemy długości podstaw, dzielimy przez 2 (obliczamy średnią długość) i mnożymy przez wysokość.
Przykład: Trapez ma podstawy o długości 5 cm i 7 cm oraz wysokość 4 cm. Jego pole wynosi ((5 cm + 7 cm) / 2) * 4 cm = 24 cm².
Praktyczna wskazówka: Pamiętaj, że wysokość trapezu to odległość między jego podstawami.
Powtórka i Ćwiczenia: Klucz do Sukcesu
Po opanowaniu teorii, najważniejsze są ćwiczenia! Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zasady i wzory.
Polecam:
- Rozwiązywanie zadań z podręcznika.
- Szukanie dodatkowych ćwiczeń w Internecie.
- Powtarzanie wzorów na głos, żeby je zapamiętać.
- Praca z kartkami, na których narysowane są figury geometryczne i wyznaczanie pól.
Pamiętaj, że regularna praca jest ważniejsza niż jednorazowe "zakuwanie" przed sprawdzianem. Krótkie, ale systematyczne sesje nauki przyniosą lepsze efekty.
Strategie na Sprawdzian: Jak Zyskać Pewność Siebie?
Na sam sprawdzian warto przygotować się mentalnie i strategicznie:
- Przeczytaj uważnie treść każdego zadania. Zrozumienie, co dokładnie trzeba obliczyć, to połowa sukcesu!
- Wypisz dane podane w zadaniu. Ułatwi to dobór odpowiedniego wzoru.
- Narysuj figurę, jeśli nie jest podana w zadaniu. Pomaga to wizualizować problem.
- Sprawdzaj jednostki! Upewnij się, że wszystkie wymiary są podane w tej samej jednostce.
- Sprawdzaj obliczenia! Nie wstydź się użyć kalkulatora, żeby uniknąć prostych błędów rachunkowych.
- Nie panikuj! Jeśli nie wiesz, jak rozwiązać zadanie, przejdź do następnego i wróć do niego później.
Pamiętaj, że sprawdzian to tylko jeden element oceny. Nie stresuj się za bardzo! Najważniejsze, żebyś zrozumiał materiał i umiał go zastosować w praktyce. Powodzenia!
A jeśli czujesz, że nadal potrzebujesz pomocy, nie krępuj się prosić o nią nauczyciela lub rodziców. Oni na pewno chętnie Ci pomogą!