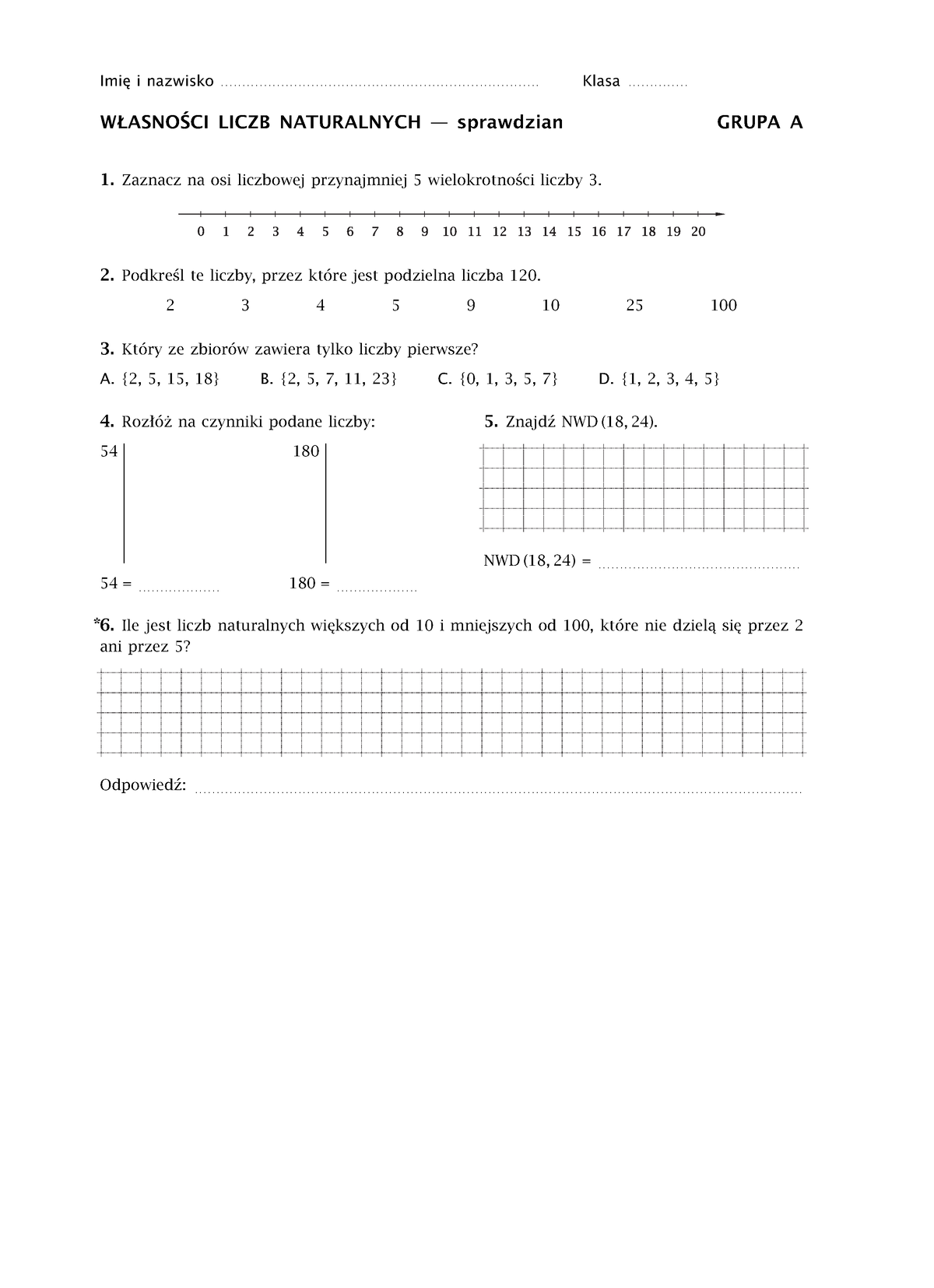
Sprawdzian Klasa 5 Matematyka Własności Liczb Naturalnych

Okej, rozumiem. Oto artykuł o własnościach liczb naturalnych, napisany w języku polskim, prostym językiem, bez tytułu, z użyciem jednej sekcji H2 i maksymalnie czterech, unikając tabel i o minimalnej długości 1000 słów.

Liczby naturalne to takie, których używamy do liczenia. Zaczynamy od 1, potem jest 2, 3, 4, 5 i tak dalej w nieskończoność. Zero czasami też się do nich zalicza, ale to zależy od tego, kto o tym mówi. Na sprawdzianie u Ciebie pewnie będzie napisane, czy zero traktujesz jako liczbę naturalną, czy nie. Ważne jest, żeby o tym pamiętać!

Dzielenie i podzielność to ważne pojęcia. Jak dzielisz jedną liczbę przez drugą i wychodzi Ci liczba całkowita (bez żadnych ułamków po przecinku), to mówimy, że pierwsza liczba jest podzielna przez drugą. Na przykład, 12 jest podzielne przez 3, bo 12 podzielone przez 3 to 4. Ale 12 nie jest podzielne przez 5, bo 12 podzielone przez 5 to 2 i jeszcze trochę (2,4).

Są pewne proste zasady, które pomagają sprawdzić, czy liczba jest podzielna przez inne liczby. To się przydaje na sprawdzianie!

Podzielność przez 2: Liczba jest podzielna przez 2, jeśli kończy się na 0, 2, 4, 6 lub 8. Czyli, jeśli ostatnia cyfra jest parzysta. Przykłady: 12, 34, 126, 1000 są podzielne przez 2. 11, 23, 125 nie są podzielne przez 2.
Podzielność przez 5: Liczba jest podzielna przez 5, jeśli kończy się na 0 lub 5. Przykłady: 25, 130, 1005 są podzielne przez 5. 12, 34, 126 nie są podzielne przez 5.
Podzielność przez 10: Liczba jest podzielna przez 10, jeśli kończy się na 0. Przykłady: 30, 140, 2000 są podzielne przez 10. 25, 135, 1001 nie są podzielne przez 10.
Podzielność przez 3: Liczba jest podzielna przez 3, jeśli suma jej cyfr jest podzielna przez 3. To brzmi trochę skomplikowanie, ale jest proste. Weźmy liczbę 123. Suma cyfr to 1 + 2 + 3 = 6. 6 jest podzielne przez 3, więc 123 też jest podzielne przez 3. Inny przykład: 456. Suma cyfr to 4 + 5 + 6 = 15. 15 jest podzielne przez 3, więc 456 też jest podzielne przez 3. A co z 124? Suma cyfr to 1 + 2 + 4 = 7. 7 nie jest podzielne przez 3, więc 124 też nie jest podzielne przez 3.
Podzielność przez 9: Podobnie jak z 3, liczba jest podzielna przez 9, jeśli suma jej cyfr jest podzielna przez 9. Na przykład: 81. Suma cyfr to 8 + 1 = 9. 9 jest podzielne przez 9, więc 81 też jest podzielne przez 9. Inny przykład: 126. Suma cyfr to 1 + 2 + 6 = 9. 9 jest podzielne przez 9, więc 126 też jest podzielne przez 9. A co z 100? Suma cyfr to 1 + 0 + 0 = 1. 1 nie jest podzielne przez 9, więc 100 też nie jest podzielne przez 9.

Liczby pierwsze i złożone to też bardzo ważne. Liczba pierwsza to taka liczba, która dzieli się tylko przez 1 i samą siebie. Na przykład: 2, 3, 5, 7, 11, 13, 17, 19... Liczba 1 nie jest liczbą pierwszą. Liczba złożona to taka liczba, która ma więcej niż dwa dzielniki (czyli dzieli się nie tylko przez 1 i samą siebie, ale też przez inne liczby). Na przykład: 4, 6, 8, 9, 10, 12...

Rozkład na czynniki pierwsze to rozpisanie liczby złożonej na iloczyn liczb pierwszych. Na przykład, rozkład liczby 12 na czynniki pierwsze to 2 x 2 x 3 (bo 2 x 2 x 3 = 12). Inny przykład: 30 = 2 x 3 x 5. Rozkładanie na czynniki pierwsze pomaga znaleźć największy wspólny dzielnik (NWD) i najmniejszą wspólną wielokrotność (NWW).

Największy Wspólny Dzielnik (NWD) i Najmniejsza Wspólna Wielokrotność (NWW)

NWD to największa liczba, która dzieli dwie (albo więcej) liczby bez reszty. Na przykład, NWD liczb 12 i 18 to 6, bo 6 jest największą liczbą, która dzieli zarówno 12 (12/6=2) jak i 18 (18/6=3).

Jak znaleźć NWD? Można wypisać wszystkie dzielniki każdej liczby i znaleźć największy wspólny. Na przykład:

Dzielniki liczby 12: 1, 2, 3, 4, 6, 12
Dzielniki liczby 18: 1, 2, 3, 6, 9, 18

Wspólne dzielniki to: 1, 2, 3, 6. Największy z nich to 6, więc NWD(12, 18) = 6.

Ale jest lepszy sposób, używając rozkładu na czynniki pierwsze:

Rozłóż obie liczby na czynniki pierwsze.
Wypisz wspólne czynniki pierwsze z najmniejszą potęgą, w jakiej występują.
Pomnóż te wspólne czynniki.

Na przykład, dla liczb 12 i 18:

12 = 2 x 2 x 3 = 2² x 3
18 = 2 x 3 x 3 = 2 x 3²

Wspólne czynniki to 2 i 3. Najmniejsza potęga 2 to 2¹ (czyli po prostu 2). Najmniejsza potęga 3 to 3¹ (czyli po prostu 3). Zatem NWD(12, 18) = 2 x 3 = 6.

NWW to najmniejsza liczba, która jest podzielna przez dwie (albo więcej) liczby. Na przykład, NWW liczb 6 i 8 to 24, bo 24 jest najmniejszą liczbą, która dzieli się zarówno przez 6 (24/6=4) jak i przez 8 (24/8=3).

Jak znaleźć NWW? Można wypisywać wielokrotności każdej liczby aż znajdziesz wspólną. Na przykład:

Wielokrotności liczby 6: 6, 12, 18, 24, 30, 36...
Wielokrotności liczby 8: 8, 16, 24, 32, 40...

Najmniejsza wspólna wielokrotność to 24, więc NWW(6, 8) = 24.

Ale znowu, jest lepszy sposób, używając rozkładu na czynniki pierwsze:

Rozłóż obie liczby na czynniki pierwsze.
Wypisz wszystkie czynniki pierwsze (wspólne i niewspólne) z największą potęgą, w jakiej występują.
Pomnóż te czynniki.

Na przykład, dla liczb 6 i 8:

6 = 2 x 3
8 = 2 x 2 x 2 = 2³

Wszystkie czynniki to 2 i 3. Największa potęga 2 to 2³ (czyli 8). Największa potęga 3 to 3¹ (czyli 3). Zatem NWW(6, 8) = 2³ x 3 = 8 x 3 = 24.

Pamiętaj, że musisz dokładnie przeczytać zadanie na sprawdzianie. Zwróć uwagę, o co pytają – czy o podzielność, czy o liczby pierwsze, czy o NWD, czy o NWW. Dobrze jest najpierw napisać sobie na kartce wszystkie dane z zadania i to, co musisz obliczyć.

Kilka dodatkowych przykładów:

Znajdź NWD(24, 36).
- 24 = 2 x 2 x 2 x 3 = 2³ x 3
- 36 = 2 x 2 x 3 x 3 = 2² x 3²
- Wspólne czynniki: 2 i 3. Najmniejsze potęgi: 2² i 3¹. NWD(24, 36) = 2² x 3 = 4 x 3 = 12.
Znajdź NWW(15, 20).
- 15 = 3 x 5
- 20 = 2 x 2 x 5 = 2² x 5
- Wszystkie czynniki: 2, 3 i 5. Największe potęgi: 2², 3¹ i 5¹. NWW(15, 20) = 2² x 3 x 5 = 4 x 3 x 5 = 60.
Czy liczba 345 jest podzielna przez 3?
- Suma cyfr: 3 + 4 + 5 = 12. 12 jest podzielne przez 3, więc 345 też jest podzielne przez 3.
Czy liczba 128 jest liczbą pierwszą?
- Nie, bo dzieli się przez 2, 4, 8, 16, 32, 64 i 128 (oprócz 1).

Pamiętaj o ćwiczeniach! Im więcej zadań zrobisz, tym lepiej zrozumiesz te zasady i tym łatwiej będzie Ci na sprawdzianie. Poproś nauczyciela o dodatkowe zadania, albo poszukaj ich w internecie. Powodzenia!