Sprawdzian Klasa 5 Matematyka Ułamki Dziesiętne

Czy zbliża się sprawdzian z ułamków dziesiętnych w klasie 5? Nie martw się! Ten artykuł jest stworzony specjalnie dla Ciebie, aby pomóc Ci zrozumieć i opanować ten temat. Skupimy się na najważniejszych zagadnieniach, które pojawiają się na sprawdzianach i pokażemy Ci, jak krok po kroku rozwiązywać zadania. Celem jest, abyś podszedł do sprawdzianu pewny siebie i gotowy na sukces!

Co to są ułamki dziesiętne i dlaczego są ważne?

Ułamki dziesiętne to sposób zapisu liczb, które są mniejsze od jedności (ale mogą być też większe, jeśli połączymy je z liczbami całkowitymi). Wykorzystują one przecinek, który oddziela część całkowitą od części ułamkowej. Na przykład, 2,5 to ułamek dziesiętny, gdzie 2 to część całkowita, a 5 to część ułamkowa.

Dlaczego ułamki dziesiętne są takie ważne? Używamy ich na co dzień! Spotykamy je w sklepach (ceny produktów), w przepisach kulinarnych (ilość składników), podczas mierzenia długości (np. w centymetrach) i w wielu innych sytuacjach. Zrozumienie ułamków dziesiętnych jest kluczowe do radzenia sobie w życiu i w dalszej edukacji matematycznej.

Najważniejsze zagadnienia na sprawdzianie

Na sprawdzianie z ułamków dziesiętnych w klasie 5 najczęściej pojawiają się następujące tematy:

Zapisywanie ułamków zwykłych jako dziesiętnych i odwrotnie. Na przykład, jak zamienić 1/2 na 0,5?
Porównywanie ułamków dziesiętnych. Który ułamek jest większy: 0,7 czy 0,75?
Dodawanie i odejmowanie ułamków dziesiętnych. Pamiętaj o właściwym ustawianiu przecinków!
Mnożenie i dzielenie ułamków dziesiętnych przez 10, 100, 1000. Jak to wpływa na położenie przecinka?
Rozwiązywanie zadań tekstowych z wykorzystaniem ułamków dziesiętnych.

Jak zamieniać ułamki zwykłe na dziesiętne i odwrotnie?

Z ułamka zwykłego na dziesiętny: Spróbuj rozszerzyć ułamek zwykły tak, aby w mianowniku (czyli na dole) mieć 10, 100 lub 1000. Na przykład:

Przykład: 1/2 = 5/10 = 0,5

Jeśli nie da się rozszerzyć, możesz podzielić licznik (górną część) przez mianownik. Użyj kalkulatora, jeśli to dozwolone na sprawdzianie.

Z ułamka dziesiętnego na zwykły: Zapisz ułamek dziesiętny jako ułamek o mianowniku 10, 100, 1000 itd., a następnie go uprość. Na przykład:

Przykład: 0,25 = 25/100 = 1/4

Porównywanie ułamków dziesiętnych

Porównując ułamki dziesiętne, zacznij od porównania części całkowitych. Jeśli są takie same, porównaj cyfry po przecinku, zaczynając od tej najbliższej przecinka.

Przykład: 0,7 i 0,75. Części całkowite są równe (0). Pierwsza cyfra po przecinku jest taka sama (7). Ale 0,75 ma jeszcze jedną cyfrę (5), więc jest większy: 0,75 > 0,7

Dodawanie i odejmowanie ułamków dziesiętnych

Najważniejsze to ustawić przecinki jeden pod drugim. Dodaj lub odejmij liczby tak jak zwykle, a przecinek w wyniku umieść w tym samym miejscu.

Przykład: 2,3 + 1,45 = ? Ustaw to tak:

       2,30
    + 1,45
    -------
       3,75

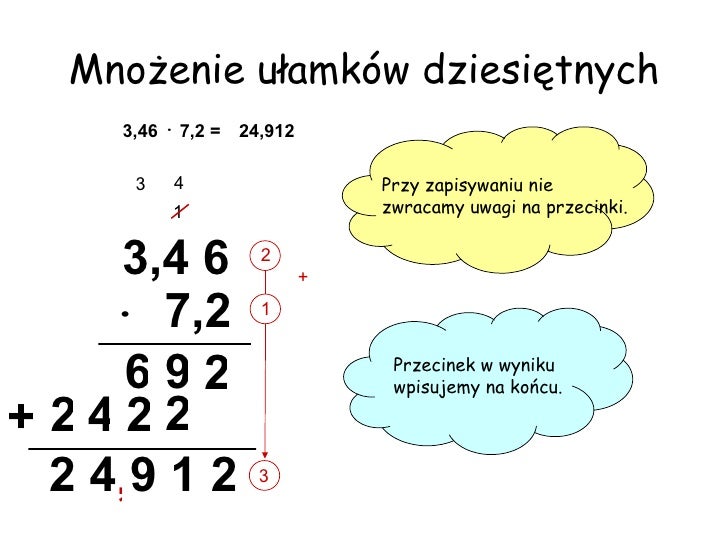
Mnożenie i dzielenie przez 10, 100, 1000

Mnożąc ułamek dziesiętny przez 10, 100 lub 1000, przesuwamy przecinek w prawo o odpowiednią liczbę miejsc (tyle, ile jest zer w liczbie, przez którą mnożymy). Dzieląc, przesuwamy przecinek w lewo.

Przykłady:

2,5 * 10 = 25
2,5 * 100 = 250
2,5 / 10 = 0,25
2,5 / 100 = 0,025

Zadania tekstowe – jak je rozwiązywać?

Czytaj uważnie treść zadania. Zastanów się, o co pytają. Wybierz odpowiednie działania (dodawanie, odejmowanie, mnożenie lub dzielenie). Wykonaj obliczenia i sprawdź, czy odpowiedź ma sens.

Przykład: Ania kupiła 2,5 kg jabłek po 3,20 zł za kilogram. Ile zapłaciła?

Rozwiązanie: Mnożymy 2,5 * 3,20 = 8 zł. Odpowiedź: Ania zapłaciła 8 zł.

Jak przygotować się do sprawdzianu?

Powtórz teorię. Przejrzyj podręcznik i zeszyt.
Rozwiąż zadania. Im więcej, tym lepiej! Zacznij od łatwiejszych, a potem przejdź do trudniejszych.
Poproś o pomoc. Jeśli masz pytania, zapytaj nauczyciela, rodziców lub kolegów.
Odpocznij. Nie ucz się do późnej nocy. Wyśpij się, żeby być wypoczętym na sprawdzianie.

Pamiętaj, wierzymy w Ciebie! Z odpowiednim przygotowaniem i nastawieniem dasz radę świetnie napisać sprawdzian z ułamków dziesiętnych. Powodzenia!