Sprawdzian Klasa 4 Ulamki Zwykle

Rozumiem, że zbliża się sprawdzian z ułamków zwykłych w klasie 4. Pewnie czujesz lekką presję, a może nawet stres? To zupełnie normalne! Ułamki na początku mogą wydawać się trochę zagmatwane, ale z odpowiednim podejściem i odrobiną praktyki, na pewno sobie poradzisz. Ten artykuł ma Ci w tym pomóc. Postaramy się wszystko wyjaśnić krok po kroku, tak abyś zrozumiał/a, o co w tych ułamkach chodzi i bez problemu rozwiązał/a zadania na sprawdzianie.

Ułamki Zwykłe – Dlaczego Są Takie Ważne?

Możesz sobie pomyśleć: "Po co mi te ułamki? Kiedy ja ich użyję w prawdziwym życiu?". Odpowiedź brzmi: często! Wyobraź sobie, że dzielisz pizzę ze znajomymi. Każdy dostaje kawałek, czyli ułamek całej pizzy. Albo kiedy mama piecze ciasto i mówi, żeby wsypać pół szklanki mąki – to też ułamek! Ułamki są wszędzie wokół nas, w życiu codziennym, w przepisach kulinarnych, przy mierzeniu, w sporcie (np. czas w ułamkach sekundy).

Zrozumienie ułamków pomaga również w innych dziedzinach matematyki. Bez ułamków trudno poradzić sobie z procentami, proporcjami, czy nawet bardziej zaawansowanymi zagadnieniami. To podstawa, na której buduje się dalsza wiedza matematyczna.

Czym Właściwie Jest Ułamek Zwykły?

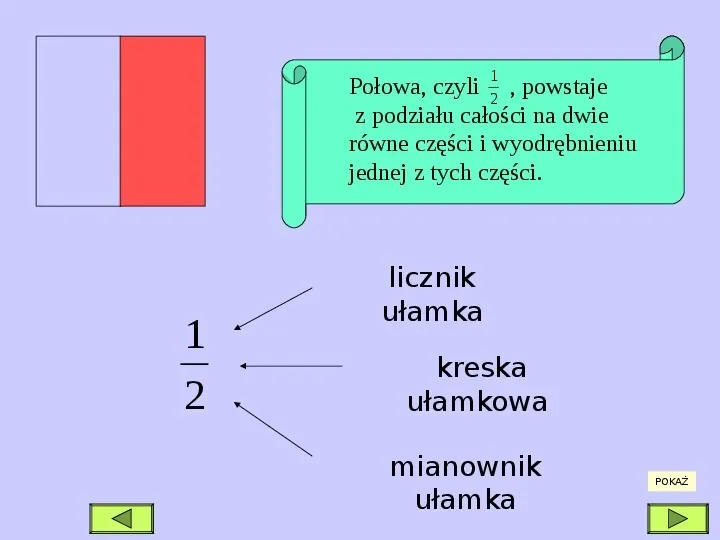
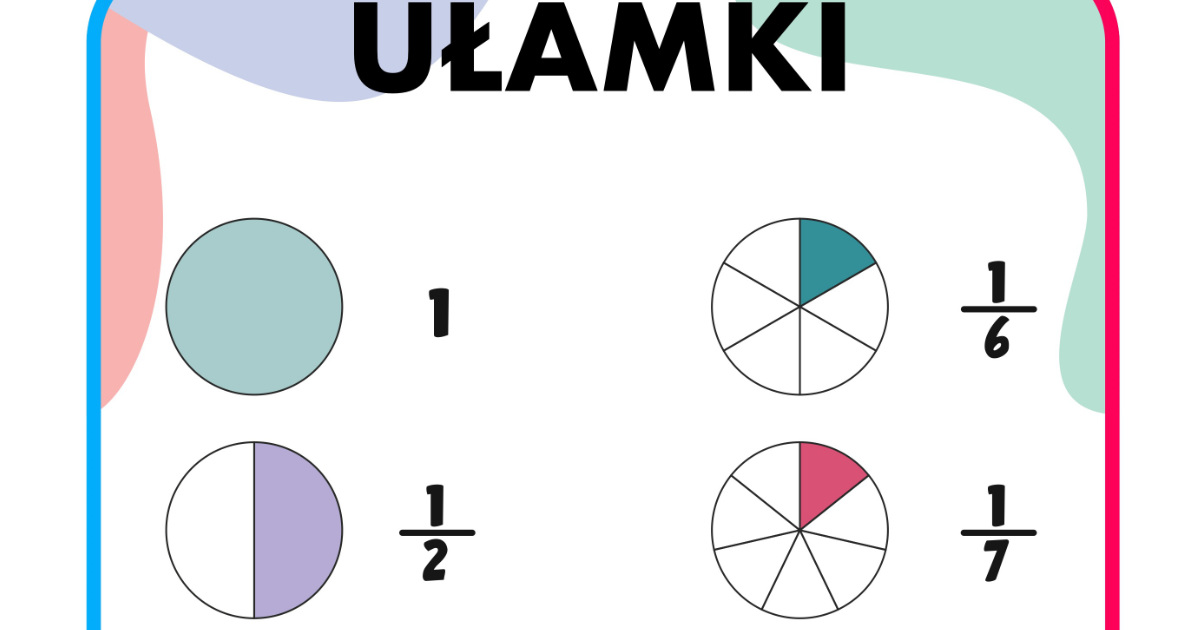
Ułamek zwykły to sposób na zapisanie części całości. Składa się z dwóch liczb, które oddziela kreska ułamkowa:

• Licznik – liczba znajdująca się nad kreską ułamkową. Mówi nam, ile części bierzemy pod uwagę.
• Mianownik – liczba znajdująca się pod kreską ułamkową. Mówi nam, na ile równych części została podzielona całość.

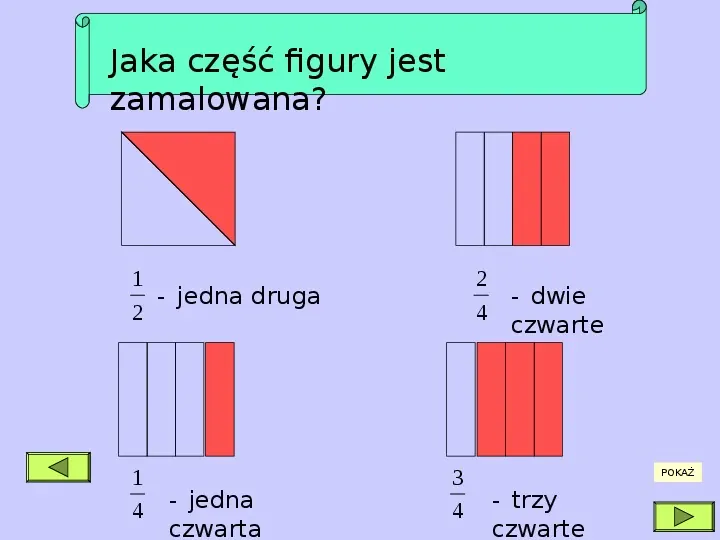
Na przykład, ułamek ½ (jedna druga) oznacza, że całość została podzielona na dwie równe części i bierzemy jedną z nich. Ułamek ¾ (trzy czwarte) oznacza, że całość została podzielona na cztery równe części i bierzemy trzy z nich.

Pomyśl o czekoladzie podzielonej na osiem kostek. Jeśli zjesz dwie kostki, to zjadłeś 2/8 (dwie ósme) czekolady.

Rodzaje Ułamków Zwykłych

Ważne jest, aby znać różne rodzaje ułamków:

• Ułamek właściwy – licznik jest mniejszy niż mianownik (np. 2/5, 7/10). Taki ułamek jest zawsze mniejszy od 1.
• Ułamek niewłaściwy – licznik jest większy lub równy mianownikowi (np. 5/2, 8/8). Taki ułamek jest większy lub równy 1.
• Liczba mieszana – składa się z liczby całkowitej i ułamka właściwego (np. 1 ½, 3 ¾). Liczba mieszana to inaczej zapis ułamka niewłaściwego.

Zamiana Ułamków Niewłaściwych na Liczby Mieszane i Odwrotnie

Umiejętność zamiany ułamków niewłaściwych na liczby mieszane i odwrotnie jest bardzo przydatna. Jak to zrobić?

Zamiana Ułamka Niewłaściwego na Liczbę Mieszaną:

1. Podziel licznik przez mianownik.
2. Wynik dzielenia (bez reszty) to liczba całkowita.
3. Reszta z dzielenia to licznik nowego ułamka. Mianownik pozostaje ten sam.

Przykład: Zamieńmy ułamek 7/3 na liczbę mieszaną.

1. 7 podzielone przez 3 to 2 i reszta 1.
2. Liczba całkowita to 2.
3. Licznik nowego ułamka to 1, a mianownik to 3.
4. Zatem 7/3 = 2 ⅓

Zamiana Liczby Mieszanej na Ułamek Niewłaściwy:

1. Pomnóż liczbę całkowitą przez mianownik.
2. Dodaj wynik do licznika.
3. Mianownik pozostaje ten sam.

Przykład: Zamieńmy liczbę mieszaną 1 ¾ na ułamek niewłaściwy.

1. 1 pomnożone przez 4 to 4.
2. 4 dodać 3 to 7.
3. Mianownik to 4.
4. Zatem 1 ¾ = 7/4

Porównywanie Ułamków

Czasami trzeba porównać, który ułamek jest większy, a który mniejszy. Są na to różne sposoby:

• Porównywanie ułamków o tym samym mianowniku – Wtedy większy jest ten ułamek, który ma większy licznik. Na przykład, 3/5 jest większe niż 1/5.
• Porównywanie ułamków o tym samym liczniku – Wtedy większy jest ten ułamek, który ma mniejszy mianownik. Na przykład, 2/3 jest większe niż 2/5.
• Sprowadzanie ułamków do wspólnego mianownika – Jest to najbardziej uniwersalna metoda. Znajdujemy wspólny mianownik (najczęściej najmniejszą wspólną wielokrotność mianowników) i sprowadzamy do niego oba ułamki. Następnie porównujemy liczniki.

Przykład: Porównajmy ułamki ¼ i ⅖. Wspólny mianownik to 20. Wtedy ¼ = 5/20, a ⅖ = 8/20. Zatem ⅖ jest większe niż ¼.

Działania na Ułamkach

Kolejny ważny temat to działania na ułamkach. Omówmy dodawanie, odejmowanie, mnożenie i dzielenie.

Dodawanie i Odejmowanie Ułamków

• Dodawanie i odejmowanie ułamków o tym samym mianowniku – Dodajemy lub odejmujemy liczniki, a mianownik pozostaje ten sam.
• Dodawanie i odejmowanie ułamków o różnych mianownikach – Najpierw musimy sprowadzić ułamki do wspólnego mianownika, a następnie dodać lub odjąć liczniki.

Przykład: ½ + ¼ = 2/4 + ¼ = 3/4. ⅗ - ⅕ = ⅖

Mnożenie Ułamków

Mnożenie ułamków jest stosunkowo proste. Mnożymy licznik przez licznik i mianownik przez mianownik.

Przykład: ½ * ⅓ = (1*1) / (2*3) = 1/6

Dzielenie Ułamków

Dzielenie ułamków to mnożenie przez odwrotność drugiego ułamka. Odwrotność ułamka to zamiana licznika z mianownikiem.

Przykład: ½ : ¼ = ½ * 4/1 = (1*4) / (2*1) = 4/2 = 2

Upraszczanie Ułamków (Skracanie)

Upraszczanie ułamków, czyli skracanie, polega na podzieleniu licznika i mianownika przez ich wspólny dzielnik. Skracamy ułamki, aby przedstawić je w najprostszej postaci. Ułamek jest nieskracalny, jeśli licznik i mianownik nie mają już żadnych wspólnych dzielników (poza 1).

Przykład: Ułamek 4/8 możemy skrócić, dzieląc licznik i mianownik przez 4. Otrzymujemy wtedy ½.

Najczęstsze Błędy na Sprawdzianie z Ułamków i Jak Ich Unikać

Warto być świadomym, jakie błędy najczęściej popełniają uczniowie, aby ich unikać:

• Zapominanie o sprowadzaniu ułamków do wspólnego mianownika przy dodawaniu i odejmowaniu. Zawsze sprawdzaj, czy mianowniki są takie same!
• Błędy przy zamianie ułamków niewłaściwych na liczby mieszane i odwrotnie. Upewnij się, że dobrze wykonałeś/aś dzielenie lub mnożenie.
• Błędy przy dzieleniu ułamków – zapominanie o odwróceniu drugiego ułamka. Pamiętaj: dzielenie to mnożenie przez odwrotność!
• Nieupraszczanie ułamków – Zawsze sprawdzaj, czy ułamek da się jeszcze skrócić.
• Brak uważności przy przepisywaniu liczb – niby proste, ale zdarza się!

Jak Się Skutecznie Uczyć do Sprawdzianu z Ułamków?

Oto kilka wskazówek, które pomogą Ci przygotować się do sprawdzianu:

• Zacznij od podstaw – Upewnij się, że rozumiesz, czym jest ułamek i jakie są jego rodzaje.
• Ćwicz, ćwicz, ćwicz! – Im więcej zadań rozwiążesz, tym lepiej zrozumiesz zasady działania na ułamkach. Skorzystaj z podręcznika, zbioru zadań, a także z internetowych zasobów.
• Rozwiązuj zadania krok po kroku – Nie spiesz się! Zapisuj wszystkie kroki rozwiązania, aby uniknąć błędów.
• Sprawdzaj swoje odpowiedzi – Porównaj swoje rozwiązania z odpowiedziami w podręczniku lub zbiorze zadań. Jeśli popełniłeś/aś błąd, spróbuj go znaleźć i zrozumieć, dlaczego tak się stało.
• Poproś o pomoc – Jeśli masz problem z jakimś zagadnieniem, nie bój się poprosić o pomoc nauczyciela, rodzica lub kolegi/koleżanki.
• Powtarzaj regularnie – Nie zostawiaj nauki na ostatnią chwilę! Powtarzaj materiał regularnie, aby utrwalić wiedzę.
• Wykorzystuj ułamki w życiu codziennym – Przygotowując posiłki, dzieląc się czymś ze znajomymi, staraj się wykorzystywać ułamki w praktyce.

Przykładowe Zadania na Sprawdzian z Ułamków

Oto kilka przykładów zadań, które mogą pojawić się na sprawdzianie:

1. Zamień ułamek niewłaściwy 11/4 na liczbę mieszaną.
2. Zamień liczbę mieszaną 2 ⅓ na ułamek niewłaściwy.
3. Porównaj ułamki ⅗ i ¾. Który jest większy?
4. Oblicz: ½ + ⅓ = ?
5. Oblicz: ¾ - ⅕ = ?
6. Oblicz: ⅔ * ¼ = ?
7. Oblicz: ⅗ : ½ = ?
8. Skróć ułamek 6/12.

Spróbuj rozwiązać te zadania samodzielnie! Jeśli będziesz miał/a problem, wróć do wcześniejszych części artykułu i przypomnij sobie zasady działania na ułamkach.

Podsumowanie

Ułamki zwykłe to ważny temat w matematyce, który warto dobrze zrozumieć. Mam nadzieję, że ten artykuł pomógł Ci uporządkować wiedzę i przygotować się do sprawdzianu. Pamiętaj, że kluczem do sukcesu jest regularna nauka i rozwiązywanie zadań. Nie bój się pytać o pomoc, jeśli masz jakieś wątpliwości. Życzę Ci powodzenia na sprawdzianie! Wierzę w Ciebie!

A teraz, po przeczytaniu tego artykułu, jakie zadanie z ułamków rozwiążesz jako pierwsze?