Sprawdzian Gwo Trojkaty Prostokatne Gimnazjum

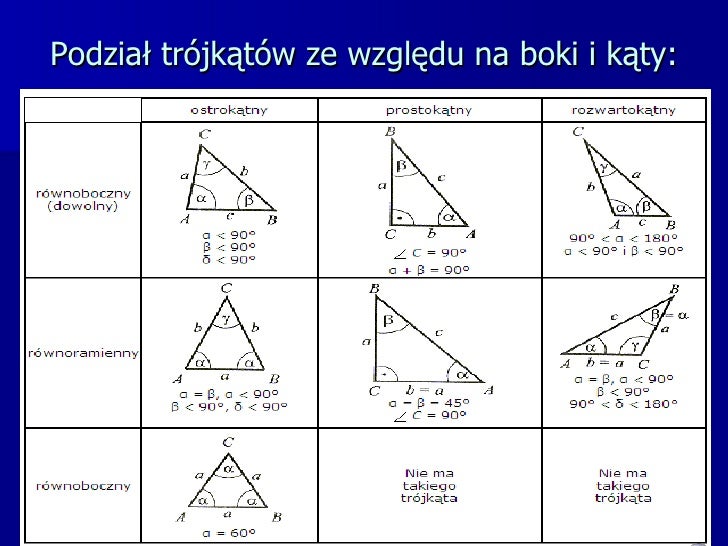
Zacznijmy od podstaw. Czym jest trójkąt prostokątny? To trójkąt, w którym jeden z kątów jest prosty, czyli ma miarę 90 stopni. Bok leżący naprzeciwko kąta prostego nazywamy przeciwprostokątną. Pozostałe dwa boki to przyprostokątne. Pamiętaj o tym! To kluczowe.
Teraz, najważniejsze twierdzenie. Twierdzenie Pitagorasa. Mówi ono, że w trójkącie prostokątnym suma kwadratów długości przyprostokątnych jest równa kwadratowi długości przeciwprostokątnej. Możemy to zapisać tak: a2 + b2 = c2, gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej. Brzmi skomplikowanie? Spokojnie, zaraz damy przykład.
Wyobraźmy sobie trójkąt prostokątny. Jedna przyprostokątna ma długość 3 cm, druga 4 cm. Ile wynosi długość przeciwprostokątnej? Używamy twierdzenia Pitagorasa: 32 + 42 = c2, czyli 9 + 16 = c2, a więc 25 = c2. Pierwiastek kwadratowy z 25 to 5, więc przeciwprostokątna ma długość 5 cm. Proste, prawda?
Funkcje Trygonometryczne
W trójkątach prostokątnych mamy też do czynienia z funkcjami trygonometrycznymi. To sinus, cosinus, tangens i cotangens. Definiują one zależności między kątami ostrymi trójkąta a długościami jego boków. Sinus kąta to stosunek długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przeciwprostokątnej. Cosinus to stosunek długości przyprostokątnej przyległej do kąta do długości przeciwprostokątnej. Tangens to stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przyprostokątnej przyległej do kąta. Cotangens to odwrotność tangensa.
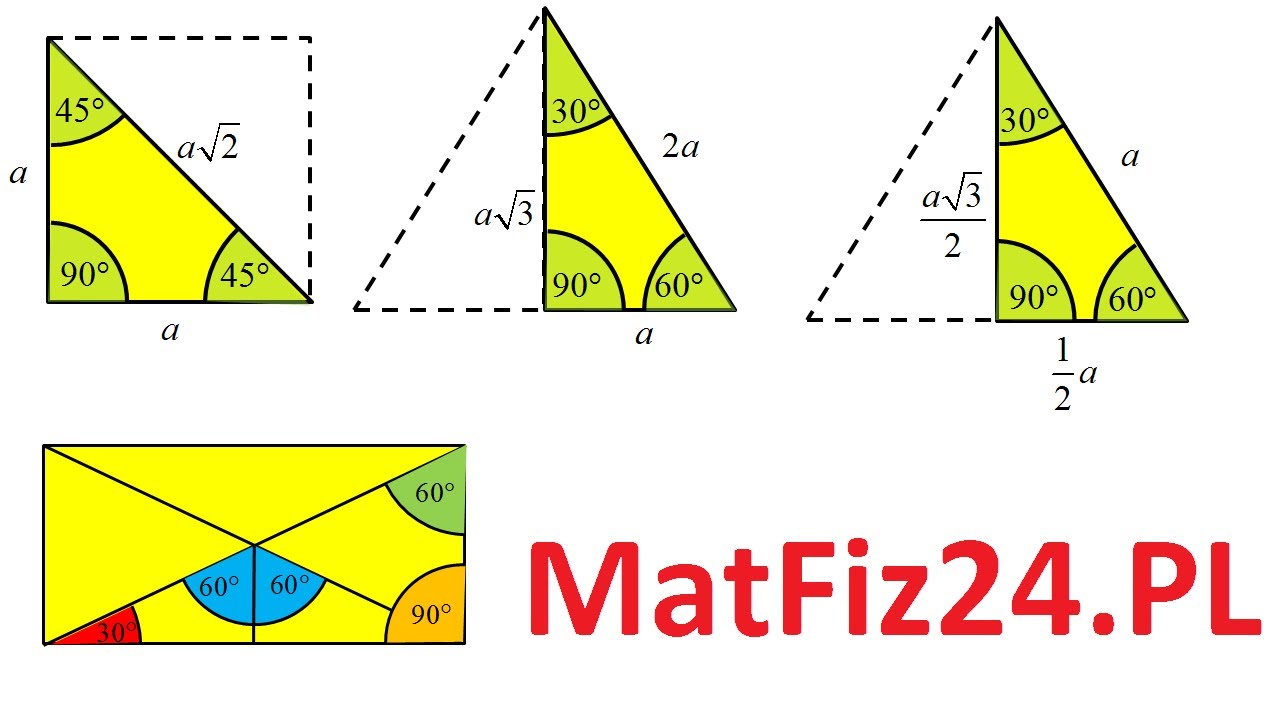
Dzięki funkcjom trygonometrycznym możemy obliczać miary kątów w trójkącie prostokątnym, znając długości boków, lub obliczać długości boków, znając miary kątów. Na przykład, jeśli znamy sinus kąta i długość przeciwprostokątnej, możemy obliczyć długość przyprostokątnej leżącej naprzeciwko tego kąta. Warto zapamiętać wartości funkcji trygonometrycznych dla kątów 30°, 45° i 60°.
Praktyczne Zastosowania
Trójkąty prostokątne i twierdzenie Pitagorasa mają wiele zastosowań w życiu codziennym. Wykorzystuje się je w budownictwie, np. do wyznaczania kątów prostych. Używają ich geodeci do pomiarów terenowych. Nawet w nawigacji, aby obliczyć odległości i kierunki, wykorzystuje się trójkąty prostokątne. Jak widzisz, wiedza o trójkątach prostokątnych przydaje się w wielu dziedzinach.
"Matematyka jest królową nauk, a arytmetyka królową matematyki." - Carl Friedrich Gauss
Ćwicz i rozwiązuj zadania. Im więcej przykładów przerobisz, tym lepiej zrozumiesz zasady dotyczące trójkątów prostokątnych. Powodzenia na sprawdzianie!