Sprawdzian Funkcja Logarytmiczna I Wykładnicza

Witaj! Chcesz lepiej zrozumieć funkcje logarytmiczne i wykładnicze? Świetnie trafiłeś! Zacznijmy od podstaw, bo zrozumienie definicji to klucz do sukcesu na Sprawdzianie Funkcja Logarytmiczna I Wykładnicza.

Definicja – Podstawa wszystkiego

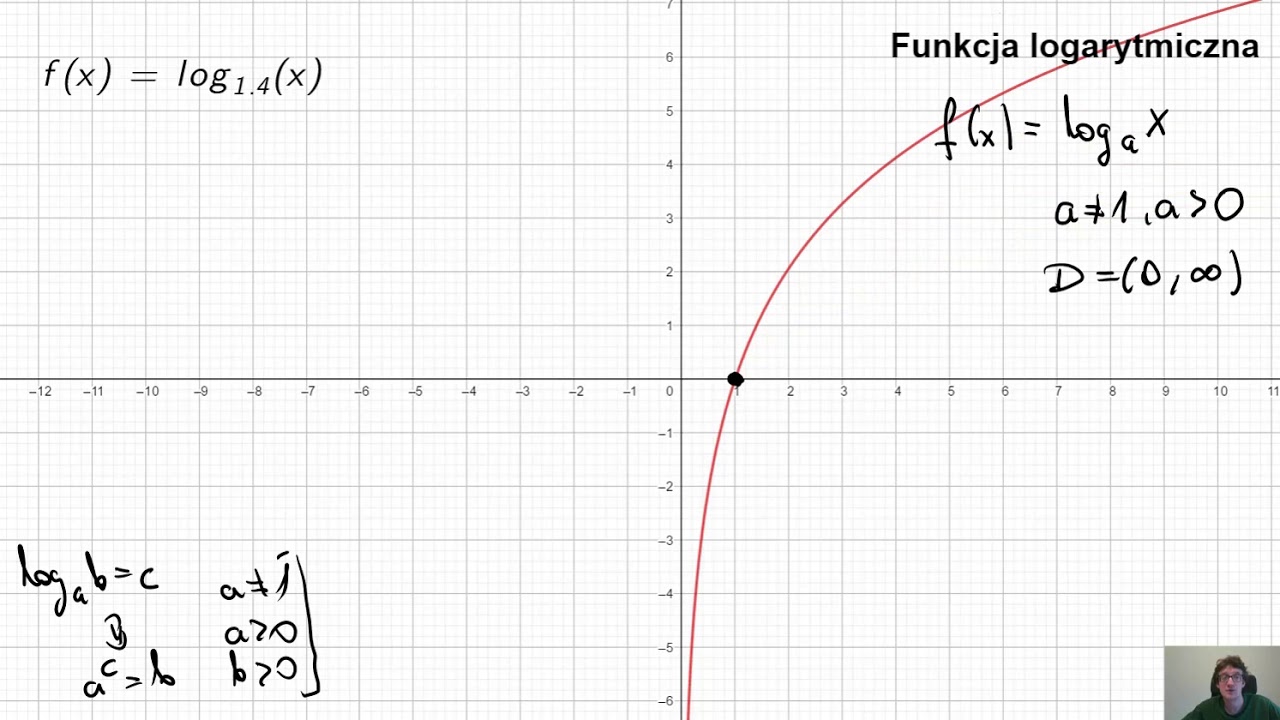
Najważniejsza rzecz to zdefiniowanie, czym są te funkcje. Funkcja wykładnicza to funkcja postaci f(x) = a^x, gdzie a jest liczbą dodatnią różną od 1 (a > 0 i a ≠ 1). x jest zmienną niezależną (argumentem funkcji). Natomiast funkcja logarytmiczna to funkcja odwrotna do funkcji wykładniczej. Zapisujemy ją jako f(x) = log_a(x), gdzie a nazywamy podstawą logarytmu i obowiązują te same zasady co dla funkcji wykładniczej (a > 0 i a ≠ 1), a x musi być liczbą dodatnią (x > 0). Mówiąc prościej, log_a(x) to odpowiedź na pytanie: do jakiej potęgi muszę podnieść a, żeby otrzymać x?

Własności Funkcji Wykładniczej

Funkcja wykładnicza f(x) = a^x, ma kilka kluczowych własności:

Jeśli a > 1, funkcja jest rosnąca. Oznacza to, że im większy x, tym większa wartość funkcji. Np. f(x) = 2^x. Dla x=2, f(x) = 4, a dla x=3, f(x) = 8.
Jeśli 0 < a < 1, funkcja jest malejąca. Oznacza to, że im większy x, tym mniejsza wartość funkcji. Np. f(x) = (1/2)^x. Dla x=2, f(x) = 1/4, a dla x=3, f(x) = 1/8.
Funkcja wykładnicza zawsze przyjmuje wartości dodatnie, niezależnie od wartości x.
Wykres funkcji wykładniczej przecina oś OY w punkcie (0, 1), bo a⁰ = 1 dla każdego a.

Własności Funkcji Logarytmicznej

Funkcja logarytmiczna f(x) = log_a(x) także ma charakterystyczne cechy:

Jeśli a > 1, funkcja jest rosnąca.
Jeśli 0 < a < 1, funkcja jest malejąca.
Funkcja logarytmiczna jest zdefiniowana tylko dla x > 0 (liczb dodatnich).
Wykres funkcji logarytmicznej przecina oś OX w punkcie (1, 0), bo log_a(1) = 0 dla każdego a.

Prawa Logarytmów

Znajomość praw logarytmów jest kluczowa do rozwiązywania zadań. Oto najważniejsze:

log_a(xy) = log_a(x) + log_a(y) (Logarytm iloczynu to suma logarytmów)
log_a(x/y) = log_a(x) - log_a(y) (Logarytm ilorazu to różnica logarytmów)
log_a(x^r) = r * log_a(x) (Logarytm potęgi)
log_a(a) = 1
log_a(1) = 0

Praktyczne Zastosowania

Funkcje logarytmiczne i wykładnicze mają mnóstwo zastosowań w życiu codziennym i nauce:

Oprocentowanie w bankach: Wzrost oszczędności na koncie często opisuje się funkcją wykładniczą (wzrost procentu składanego).
Skala Richtera: Do opisu siły trzęsień ziemi używa się skali logarytmicznej.
Biologia: Wzrost populacji bakterii często modeluje się funkcją wykładniczą. Rozpad radioaktywny również opisywany jest funkcją wykładniczą.
Chemia: pH roztworów, czyli miara kwasowości lub zasadowości, jest definiowane za pomocą logarytmu.

Mam nadzieję, że ten przewodnik pomoże Ci lepiej przygotować się do Sprawdzianu Funkcja Logarytmiczna I Wykładnicza! Pamiętaj, praktyka czyni mistrza, więc rozwiązuj jak najwięcej zadań. Powodzenia!