Sprawdzian Funkcja Kwadratowa Liceum Nowa Era

Przygotowanie sprawdzianu z funkcji kwadratowej dla uczniów liceum to wyzwanie. Chcemy sprawdzić ich wiedzę, ale również utrwalić ważne umiejętności. Skupmy się na kilku kluczowych aspektach i metodach.

Kluczowe zagadnienia sprawdzianu

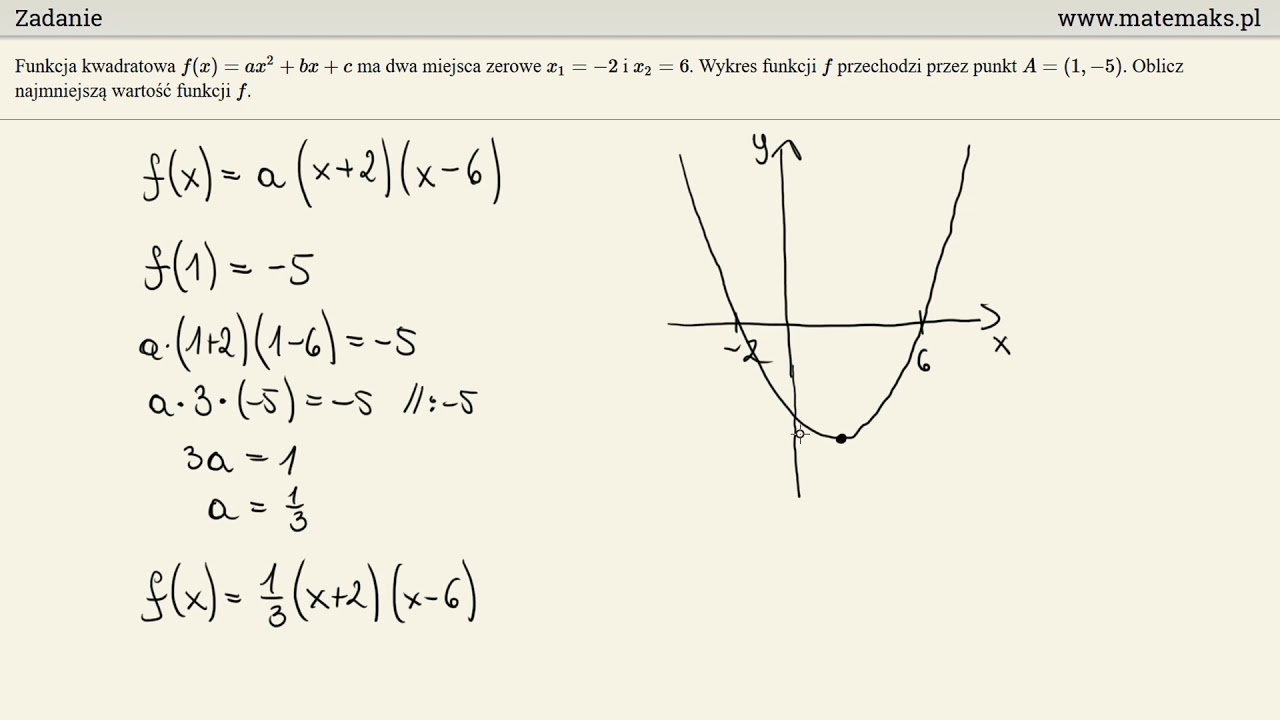
Postać ogólna, kanoniczna i iloczynowa to fundament. Upewnijmy się, że uczniowie swobodnie przechodzą między nimi. Znajomość wzorów Viète'a jest niezbędna. Ich poprawne stosowanie świadczy o dogłębnym zrozumieniu zależności między pierwiastkami a współczynnikami.

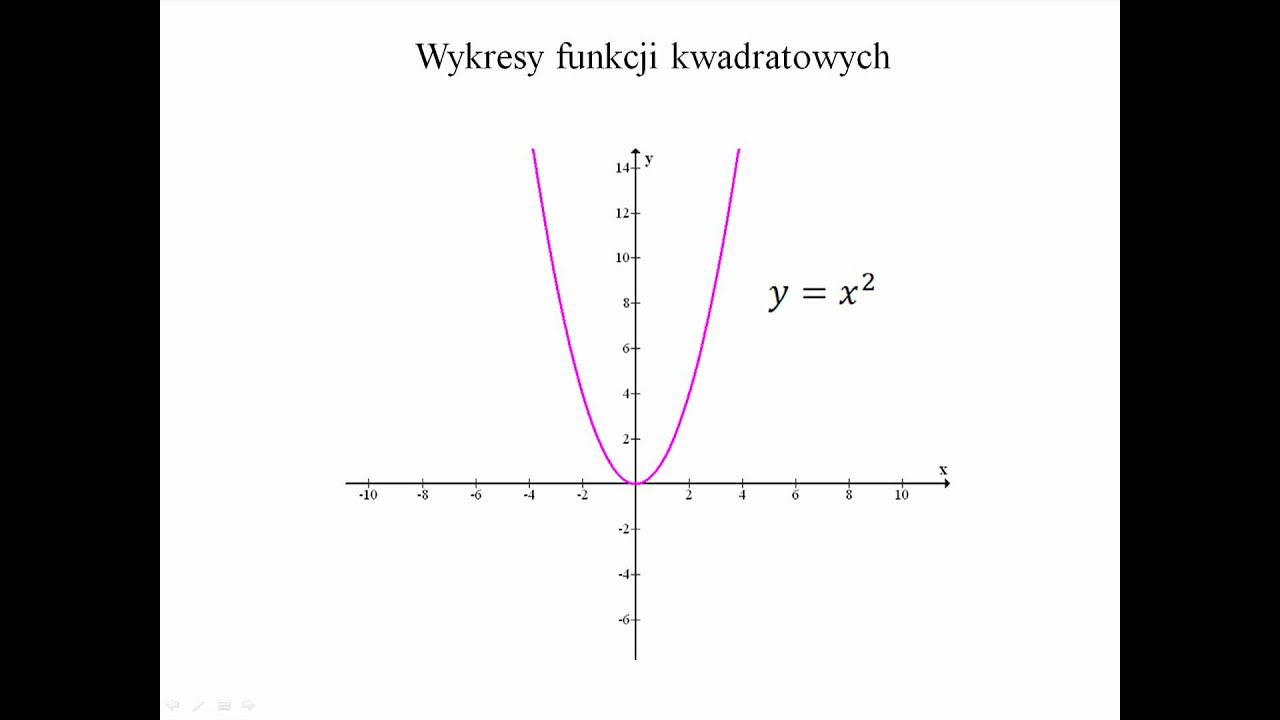
Wykresem funkcji kwadratowej jest parabola. Uczniowie powinni umieć ją szkicować na podstawie różnych danych. Wierzchołek, miejsca zerowe, punkt przecięcia z osią Y – to punkty, które ułatwiają rysowanie. Określanie monotoniczności i zbioru wartości to kolejne ważne umiejętności.

Równania i nierówności kwadratowe to naturalne rozszerzenie tematu. Rozwiązywanie ich wymaga znajomości różnych metod. Metoda graficzna, algebraiczna – każda z nich ma swoje zastosowanie. Pamiętajmy o interpretacji geometrycznej rozwiązań nierówności.

Typowe błędy i jak im zapobiegać

Częstym błędem jest mylenie postaci funkcji. Postać ogólna służy do obliczania delty, a kanoniczna do odczytywania współrzędnych wierzchołka. Ćwiczenia w przekształceniach pomagają uniknąć pomyłek. Utrwalanie wiadomości jest kluczowe.

Błędy rachunkowe przy obliczaniu delty są nagminne. Uważne podstawianie do wzoru to podstawa. Częste ćwiczenia wyrabiają nawyk dokładności. Sprawdzanie obliczeń to dobra praktyka.

Interpretacja geometryczna nierówności kwadratowych sprawia trudności. Wizualizacja rozwiązania na osi liczbowej pomaga zrozumieć sens. Rysowanie paraboli i zaznaczanie obszarów spełniających nierówność ułatwia zrozumienie. Dajmy uczniom czas na zrozumienie koncepcji.

Jak uatrakcyjnić naukę funkcji kwadratowej?

Wykorzystajmy programy graficzne do rysowania wykresów. GeoGebra to doskonałe narzędzie do wizualizacji funkcji. Uczniowie mogą eksperymentować i obserwować zmiany wykresu w zależności od parametrów.

Zastosowania funkcji kwadratowej w życiu codziennym są liczne. Tor lotu piłki, mosty paraboliczne – to tylko przykłady. Pokazanie praktycznego zastosowania zwiększa motywację. Uczniowie widzą sens nauki.

Zadania z parametrem stanowią wyzwanie. Wprowadzajmy je stopniowo, zaczynając od prostych przypadków. Analiza wpływu parametru na własności funkcji rozwija myślenie analityczne. Praca zespołowa nad zadaniami z parametrem to świetny sposób na naukę.