Sprawdz Ktore Kwadraty Sa Magiczne

Witaj! Czy kiedykolwiek zastanawiałeś się, jak magiczne mogą być pewne układy liczb? Mowa o kwadratach magicznych – fascynujących konstrukcjach, które od wieków intrygują matematyków, entuzjastów łamigłówek i miłośników ezoteryki. Ten artykuł ma na celu przybliżyć Ci ideę kwadratów magicznych, wyjaśnić, jak je rozpoznawać i jak sprawdzić, czy dany kwadrat faktycznie zasługuje na miano "magicznego". Przygotuj się na podróż po świecie liczb i ich niezwykłych właściwościach!

Czym Jest Kwadrat Magiczny? Definicja i Podstawowe Właściwości

Zacznijmy od definicji. Kwadrat magiczny to kwadratowa tablica liczb (najczęściej całkowitych dodatnich) o wymiarach n x n, gdzie n oznacza rząd kwadratu. Kluczową cechą kwadratu magicznego jest to, że suma liczb w każdym wierszu, każdej kolumnie i na obu przekątnych jest taka sama. Tę sumę nazywamy stałą magiczną (czasami liczbą magiczną lub sumą magiczną) kwadratu.

Kluczowe właściwości kwadratów magicznych:

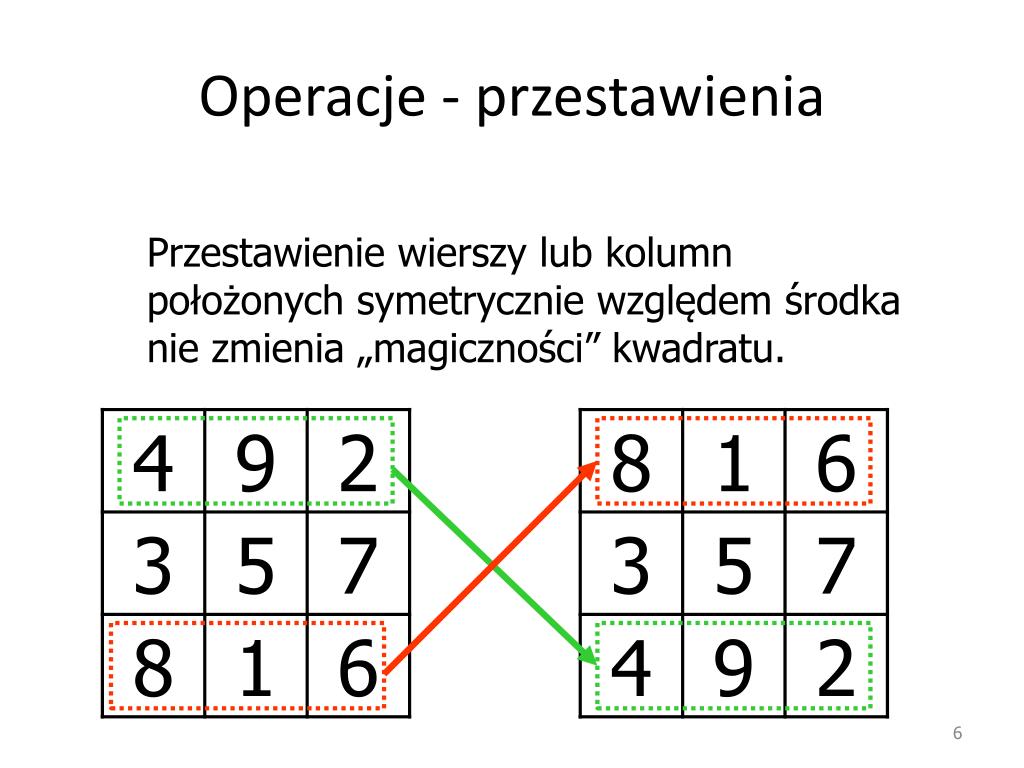
Wymiar: Kwadrat musi być kwadratowy – liczba wierszy musi być równa liczbie kolumn.
Liczby: Najczęściej używa się kolejnych liczb naturalnych, np. od 1 do n². Jednak istnieją również kwadraty magiczne, które używają innych zbiorów liczb.
Suma magiczna: Suma liczb w każdym wierszu, każdej kolumnie i na obu przekątnych musi być identyczna.

Jak Obliczyć Stałą Magiczną?

Znając rząd kwadratu (n) i fakt, że używa on kolejnych liczb naturalnych od 1 do n², możemy łatwo obliczyć stałą magiczną (M) za pomocą prostego wzoru:

M = n * (n² + 1) / 2

Na przykład, dla kwadratu magicznego rzędu 3 (n = 3), stała magiczna wynosi:

M = 3 * (3² + 1) / 2 = 3 * (9 + 1) / 2 = 3 * 10 / 2 = 15

Oznacza to, że suma liczb w każdym wierszu, każdej kolumnie i na każdej przekątnej w kwadracie magicznym rzędu 3 musi wynosić 15.

Sprawdzanie, Czy Kwadrat Jest Magiczny – Krok Po Kroku

Teraz przejdźmy do konkretów. Jak sprawdzić, czy dany kwadrat liczb jest kwadratem magicznym? Oto szczegółowa instrukcja:

Określ rząd kwadratu (n). Policz, ile wierszy i kolumn ma kwadrat. Musi to być ta sama liczba.
Sprawdź, czy kwadrat zawiera odpowiednie liczby. Upewnij się, że kwadrat zawiera liczby od 1 do n² i że każda liczba występuje tylko raz (chyba że mamy do czynienia z innym rodzajem kwadratu magicznego, np. magicznym kwadratem multiplikatywnym).
Oblicz stałą magiczną (M). Użyj wzoru M = n * (n² + 1) / 2.
Oblicz sumy wierszy. Zsumuj liczby w każdym wierszu i sprawdź, czy każda suma jest równa stałej magicznej (M).
Oblicz sumy kolumn. Zsumuj liczby w każdej kolumnie i sprawdź, czy każda suma jest równa stałej magicznej (M).
Oblicz sumy przekątnych. Zsumuj liczby na głównej przekątnej (od lewego górnego rogu do prawego dolnego rogu) i na drugiej przekątnej (od prawego górnego rogu do lewego dolnego rogu). Sprawdź, czy obie sumy są równe stałej magicznej (M).

Jeśli wszystkie powyższe warunki są spełnione, to kwadrat jest kwadratem magicznym! Jeśli choć jeden warunek nie jest spełniony, kwadrat nie jest magiczny.

Przykład Sprawdzania Kwadratu Magicznego

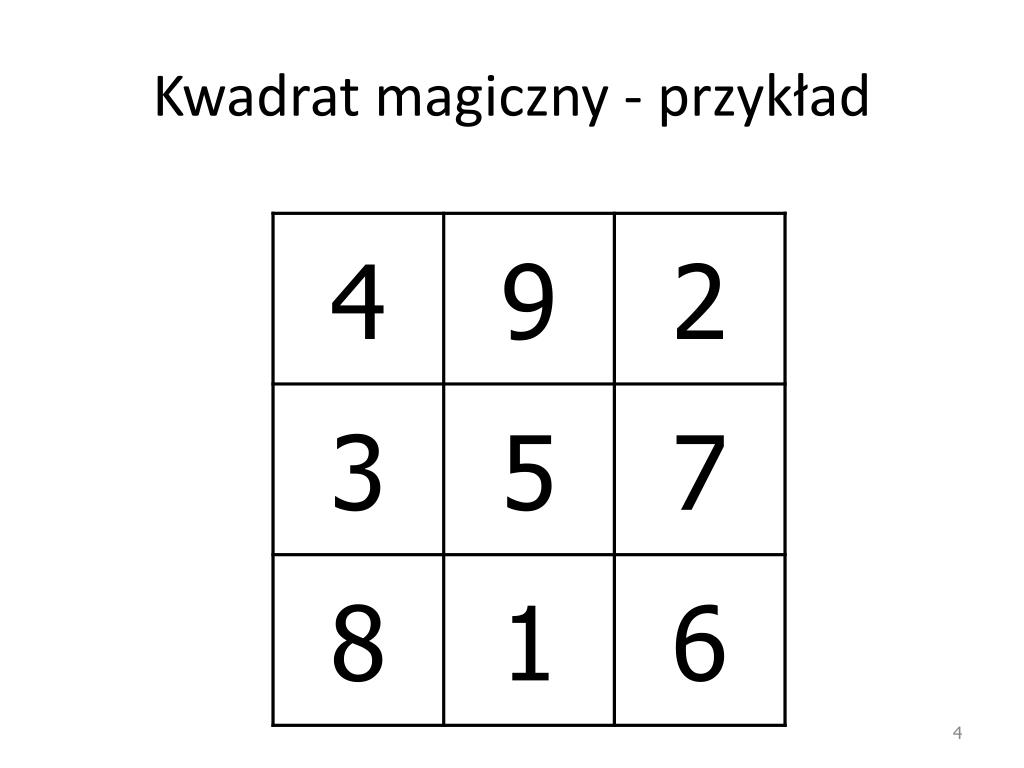
Weźmy przykładowy kwadrat:

8  1  6
3  5  7
4  9  2

Rząd kwadratu: n = 3
Liczby: Kwadrat zawiera liczby od 1 do 9, każda występuje raz.
Stała magiczna: M = 3 * (3² + 1) / 2 = 15
Sumy wierszy:
- 8 + 1 + 6 = 15
- 3 + 5 + 7 = 15
- 4 + 9 + 2 = 15
Sumy kolumn:
- 8 + 3 + 4 = 15
- 1 + 5 + 9 = 15
- 6 + 7 + 2 = 15
Sumy przekątnych:
- 8 + 5 + 2 = 15
- 6 + 5 + 4 = 15

Ponieważ wszystkie warunki są spełnione, ten kwadrat jest kwadratem magicznym.

Trudności i Pułapki Podczas Sprawdzania

Podczas sprawdzania, czy dany kwadrat jest magiczny, łatwo popełnić błędy. Oto kilka typowych trudności i pułapek, na które warto zwrócić uwagę:

Błędy w obliczeniach: Najczęstszy błąd to po prostu pomyłka w dodawaniu liczb. Zawsze sprawdzaj swoje obliczenia dokładnie!
Pominięcie wiersza, kolumny lub przekątnej: Upewnij się, że sprawdziłeś wszystkie wiersze, kolumny i przekątne.
Niewłaściwy zakres liczb: Kwadrat musi zawierać odpowiednie liczby (najczęściej kolejne liczby naturalne od 1 do n²). Sprawdź to dokładnie.
Powtarzające się liczby: W standardowych kwadratach magicznych każda liczba powinna wystąpić tylko raz. Jeśli liczba powtarza się, kwadrat prawdopodobnie nie jest magiczny (chyba że mamy do czynienia ze specjalnym rodzajem kwadratu magicznego).
Pomylenie wierszy z kolumnami: Podczas dodawania liczb w wierszach i kolumnach łatwo się pomylić. Zachowaj ostrożność!

Aby uniknąć tych błędów, warto sprawdzić kwadrat magiczny dwa razy lub poprosić kogoś innego o sprawdzenie za Ciebie. Można również skorzystać z programów komputerowych lub kalkulatorów online, które automatycznie sprawdzają, czy dany kwadrat jest magiczny.

Kwadraty Magiczne w Kulturze i Historii

Kwadraty magiczne mają bogatą historię i od dawna fascynują ludzi na całym świecie. Znane były już w starożytnych Chinach, Indiach i krajach arabskich. Przypisywano im właściwości magiczne i używano jako amuletów ochronnych. W Europie kwadraty magiczne pojawiły się w średniowieczu i renesansie. Słynny kwadrat magiczny można zobaczyć na rycinie Melancholia I autorstwa Albrechta Dürera.

Współcześnie kwadraty magiczne są nadal popularne jako łamigłówki i zagadki matematyczne. Są również wykorzystywane w kryptografii i innych dziedzinach nauki.

Kwadraty Magiczne w Życiu Codziennym?

Choć na pierwszy rzut oka może się wydawać, że kwadraty magiczne to tylko abstrakcyjna koncepcja matematyczna, w rzeczywistości mogą mieć zastosowania w różnych dziedzinach. Przykładowo, mogą być wykorzystywane w planowaniu eksperymentów, gdzie ważne jest, aby zapewnić równomierne rozłożenie zmiennych. W kryptografii kwadraty magiczne mogą być używane do generowania kluczy szyfrujących. Co więcej, rozwiązywanie zagadek związanych z kwadratami magicznymi rozwija logiczne myślenie i umiejętność rozwiązywania problemów, które są przydatne w wielu aspektach życia.

Nawet w sztuce można znaleźć inspiracje kwadratami magicznymi. Artyści mogą wykorzystywać je jako podstawę do tworzenia interesujących kompozycji i struktur wizualnych.

Podsumowanie i Wezwanie Do Działania

Kwadraty magiczne to fascynujący obszar matematyki, który łączy w sobie elegancję, symetrię i element zaskoczenia. W tym artykule omówiliśmy definicję kwadratu magicznego, sposób obliczania stałej magicznej i krok po kroku instrukcję, jak sprawdzić, czy dany kwadrat jest magiczny. Poznaliśmy również historię kwadratów magicznych i ich potencjalne zastosowania w różnych dziedzinach.

Teraz Twoja kolej! Spróbuj stworzyć własny kwadrat magiczny lub poszukaj gotowych kwadratów i sprawdź, czy rzeczywiście są magiczne. Podziel się swoimi odkryciami z innymi! Odkryj magię liczb! Pamiętaj, że matematyka może być zarówno nauką, jak i fascynującą zabawą. Zachęcamy do dalszego zgłębiania wiedzy na temat kwadratów magicznych i innych zagadnień matematycznych.

Powodzenia w Twojej przygodzie z kwadratami magicznymi!