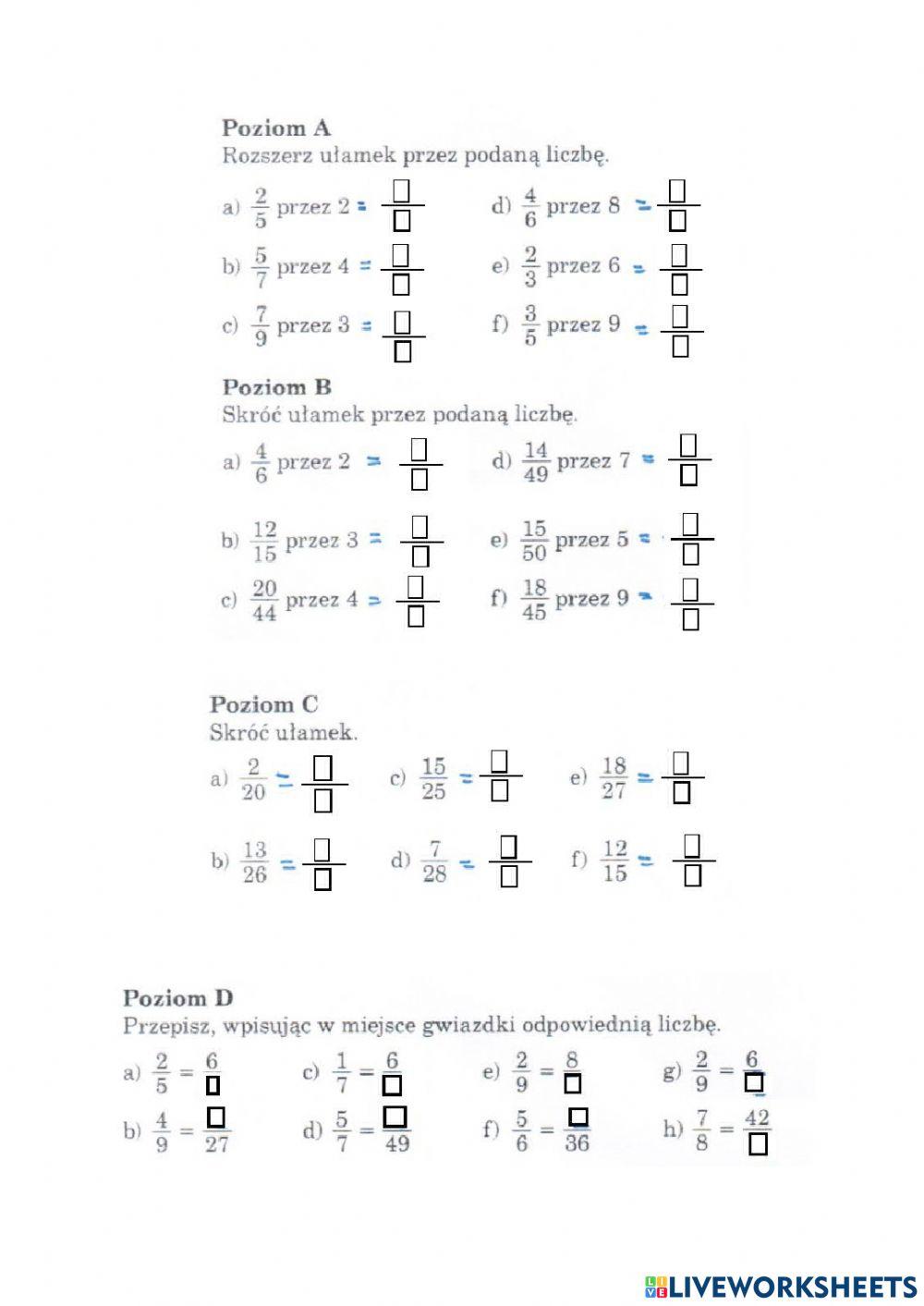
Skracanie I Rozszerzanie Ułamków Zwykłych Klasa 5 Zadania

Dobrze, postaram się jak najlepiej wytłumaczyć skracanie i rozszerzanie ułamków zwykłych w sposób zrozumiały dla ucznia klasy 5.

Ułamki zwykłe to liczby, które zapisujemy jako jedna liczba nad drugą, oddzielone kreską ułamkową. Na przykład: 1/2, 3/4, 5/8. Liczba na górze to licznik, a liczba na dole to mianownik. Mianownik mówi nam, na ile równych części podzieliliśmy całość, a licznik – ile takich części bierzemy.

Rozszerzanie Ułamków

Rozszerzanie ułamka to tak naprawdę powiększanie go, ale w taki sprytny sposób, że jego wartość się nie zmienia. Wyobraź sobie, że masz pizzę podzieloną na 4 kawałki i zjadasz jeden kawałek. Zjadłeś 1/4 pizzy. Teraz wyobraź sobie, że każdą z tych 4 części kroisz na pół. Nagle masz 8 kawałków pizzy (podwoiłeś liczbę kawałków), a ten jeden, który zjadłeś, zamienił się w dwa kawałki. Zjadłeś 2/8 pizzy. Czy zjadłeś więcej pizzy? Nie! Zjadłeś dokładnie tyle samo, tylko opisujesz to inaczej.

To właśnie jest rozszerzanie. Mnożysz zarówno licznik, jak i mianownik przez tę samą liczbę. To tak, jakbyś "powiększał" ułamek, ale zachowywał jego proporcje.

Na przykład, weźmy ułamek 1/2. Chcemy go rozszerzyć przez 3. Oznacza to, że mnożymy licznik (1) przez 3 i mianownik (2) przez 3.

1 * 3 = 3 2 * 3 = 6

Czyli 1/2 rozszerzone przez 3 to 3/6. Ułamek 1/2 i 3/6 reprezentują dokładnie tę samą wartość. Jeśli masz połowę czekolady, to jest to to samo, co trzy kawałki czekolady podzielonej na sześć części.

Inny przykład: Chcemy rozszerzyć ułamek 2/5 przez 4.

2 * 4 = 8 5 * 4 = 20

Czyli 2/5 rozszerzone przez 4 to 8/20.

Dlaczego to robimy? Rozszerzanie ułamków przydaje się, gdy chcemy porównać ułamki, które mają różne mianowniki, albo gdy chcemy je dodać lub odjąć. Żeby to zrobić, musimy sprowadzić je do wspólnego mianownika, czyli sprawić, żeby miały ten sam mianownik. A do tego potrzebujemy rozszerzania!

Skracanie Ułamków

Skracanie ułamków to proces odwrotny do rozszerzania. Zamiast powiększać licznik i mianownik, zmniejszamy je, ale tak, żeby wartość ułamka się nie zmieniła. Robimy to, dzieląc zarówno licznik, jak i mianownik przez tę samą liczbę. Ta liczba musi być dzielnikiem zarówno licznika, jak i mianownika. Dzielnik to liczba, przez którą możemy podzielić inną liczbę bez reszty.

Wyobraź sobie, że masz 6/8 pizzy. To sporo! Ale zauważasz, że zarówno 6, jak i 8 można podzielić przez 2.

6 : 2 = 3 8 : 2 = 4

Czyli 6/8 można skrócić do 3/4. Ułamek 6/8 i 3/4 reprezentują tę samą ilość pizzy. Po prostu opisujemy ją za pomocą mniejszych liczb.

Inny przykład: Weźmy ułamek 12/18. Zarówno 12, jak i 18 można podzielić przez 2, ale można je też podzielić przez 3, a nawet przez 6! Spróbujmy podzielić przez 6:

12 : 6 = 2 18 : 6 = 3

Czyli 12/18 można skrócić do 2/3. To najprostsza postać tego ułamka, ponieważ 2 i 3 nie mają już żadnych wspólnych dzielników (oprócz 1). Mówimy, że ułamek jest nieskracalny.

Jeśli nie widzisz od razu największego wspólnego dzielnika, możesz skracać ułamek stopniowo. Na przykład, zamiast od razu dzielić 12/18 przez 6, możesz najpierw podzielić przez 2:

12 : 2 = 6 18 : 2 = 9

Dostajemy 6/9. Teraz widzimy, że zarówno 6, jak i 9 można podzielić przez 3:

6 : 3 = 2 9 : 3 = 3

I znowu otrzymujemy 2/3.

Kiedy ułamek jest już skrócony do najprostszej postaci, łatwiej go porównać z innymi ułamkami i wykonywać na nim różne działania.

Jak znaleźć liczbę do skracania?

Czasami trudno od razu zobaczyć, przez jaką liczbę podzielić licznik i mianownik. Oto kilka wskazówek:

Czy liczby są parzyste? Jeśli tak, to na pewno można je podzielić przez 2.
Czy suma cyfr liczby dzieli się przez 3? Jeśli tak, to liczba dzieli się przez 3. Na przykład, w liczbie 12 suma cyfr to 1 + 2 = 3, a 3 dzieli się przez 3, więc 12 dzieli się przez 3. W liczbie 18 suma cyfr to 1 + 8 = 9, a 9 dzieli się przez 3, więc 18 dzieli się przez 3.
Czy liczba kończy się na 0 lub 5? Jeśli tak, to na pewno można ją podzielić przez 5.

Używanie tych wskazówek pomoże Ci szybciej znaleźć odpowiednią liczbę do skracania.

Praktyczne Przykłady

Spróbujmy teraz rozwiązać kilka zadań:

Rozszerz ułamek 3/7 przez 5.
- 3 * 5 = 15
- 7 * 5 = 35
Czyli 3/7 rozszerzone przez 5 to 15/35.
Skróć ułamek 20/30.
- Zarówno 20, jak i 30 kończą się na 0, więc możemy je podzielić przez 10.
- 20 : 10 = 2
- 30 : 10 = 3
Czyli 20/30 skrócone to 2/3.
Sprowadź ułamki 1/3 i 1/4 do wspólnego mianownika.
- Żeby to zrobić, musimy znaleźć liczbę, która jest podzielna zarówno przez 3, jak i przez 4. Najmniejsza taka liczba to 12.
- Musimy rozszerzyć 1/3, żeby w mianowniku otrzymać 12. 3 * 4 = 12, więc rozszerzamy 1/3 przez 4:
  - 1 * 4 = 4
  - 3 * 4 = 12
  - Czyli 1/3 rozszerzone przez 4 to 4/12.
- Musimy rozszerzyć 1/4, żeby w mianowniku otrzymać 12. 4 * 3 = 12, więc rozszerzamy 1/4 przez 3:
  - 1 * 3 = 3
  - 4 * 3 = 12
  - Czyli 1/4 rozszerzone przez 3 to 3/12.
Teraz mamy ułamki 4/12 i 3/12, które mają wspólny mianownik i możemy je łatwo porównać lub dodać.

Mam nadzieję, że teraz rozumiesz, na czym polega rozszerzanie i skracanie ułamków. Pamiętaj, że to tylko kwestia praktyki. Im więcej będziesz ćwiczyć, tym łatwiej Ci to przyjdzie!