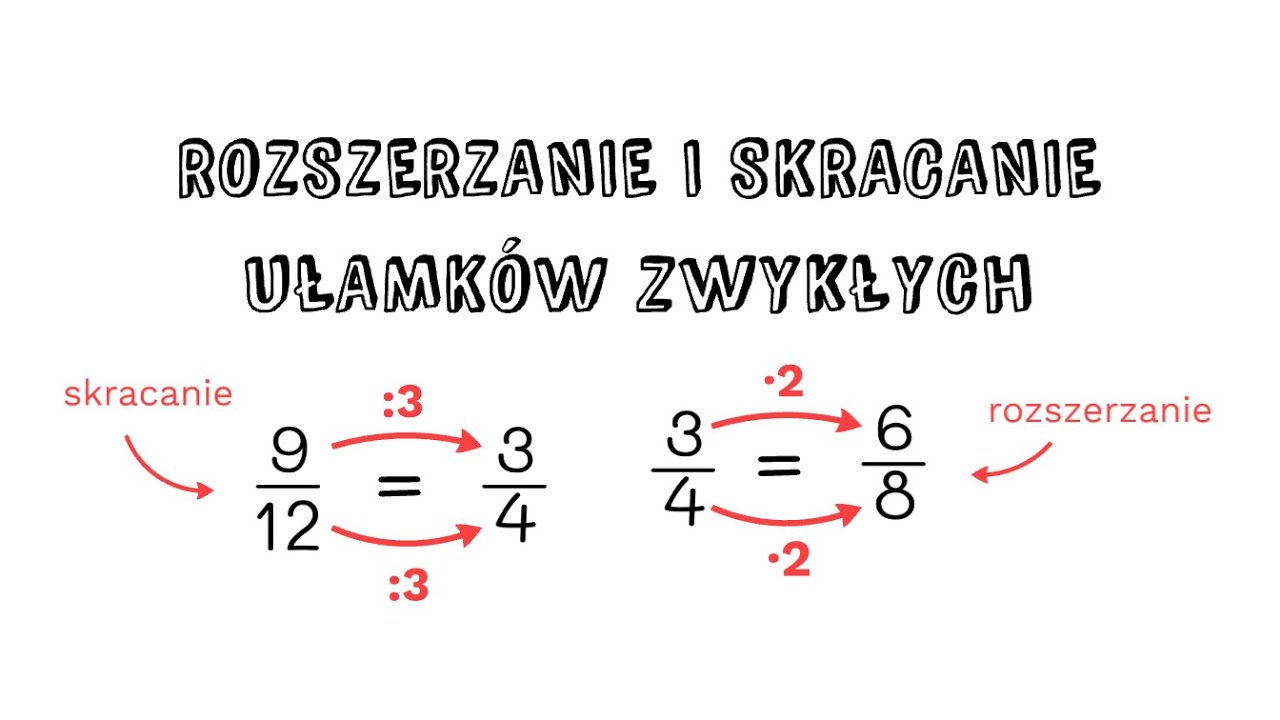
Skracanie I Rozszerzanie Ułamków Klasa 4

Witaj w świecie ułamków! W klasie czwartej rozpoczynamy fascynującą podróż po krainie liczb, które reprezentują części całości. Dziś skupimy się na dwóch bardzo ważnych umiejętnościach związanych z ułamkami: skracaniu i rozszerzaniu ułamków. Zrozumienie tych operacji jest kluczowe do dalszej nauki matematyki, szczególnie jeśli chodzi o działania na ułamkach, porównywanie ich i rozwiązywanie zadań.

Czym są Ułamki? Małe Przypomnienie

Zanim przejdziemy do skracania i rozszerzania, krótko przypomnijmy sobie, czym w ogóle jest ułamek. Ułamek to liczba, która wyraża część całości. Składa się z dwóch części:

• Licznik (górna liczba) – pokazuje, ile części całości mamy.
• Mianownik (dolna liczba) – pokazuje, na ile równych części podzielona jest całość.

Na przykład, ułamek ³/₄ (czytamy: trzy czwarte) oznacza, że całość została podzielona na cztery równe części, a my mamy trzy z tych części. Pamiętaj, że mianownik nie może być równy zero, ponieważ dzielenie przez zero jest niedozwolone!

Skracanie Ułamków: Upraszczanie Wyrażeń

Skracanie ułamków to proces upraszczania ułamka, zachowując jednocześnie jego wartość. Innymi słowy, chcemy znaleźć ułamek równy danemu, ale z mniejszymi liczbami w liczniku i mianowniku. Robimy to, dzieląc licznik i mianownik przez tę samą liczbę, która jest ich wspólnym dzielnikiem.

Jak Skracać Ułamki? Krok po Kroku

1. Znajdź wspólny dzielnik licznika i mianownika. Zazwyczaj zaczynamy od najmniejszych liczb pierwszych, takich jak 2, 3, 5, 7, i sprawdzamy, czy obie liczby są przez nie podzielne.
2. Podziel licznik i mianownik przez ten wspólny dzielnik. Otrzymasz nowy ułamek.
3. Sprawdź, czy nowy ułamek można jeszcze skrócić. Jeśli tak, powtórz kroki 1 i 2.
4. Kontynuuj skracanie, aż nie znajdziesz więcej wspólnych dzielników. Ułamek, którego już nie można skrócić, nazywamy ułamkiem nieskracalnym lub ułamkiem w postaci najprostszej.

Przykład: Skróćmy ułamek ⁸/₁₂.

• Licznik (8) i mianownik (12) są podzielne przez 2.
• Dzielimy 8 przez 2 i otrzymujemy 4. Dzielimy 12 przez 2 i otrzymujemy 6.
• Nowy ułamek to ⁴/₆.
• Czy można go jeszcze skrócić? Tak! 4 i 6 są znowu podzielne przez 2.
• Dzielimy 4 przez 2 i otrzymujemy 2. Dzielimy 6 przez 2 i otrzymujemy 3.
• Otrzymujemy ułamek ²/₃.
• Czy można go jeszcze skrócić? Nie! 2 i 3 nie mają wspólnych dzielników (poza 1).

Zatem, ⁸/₁₂ = ⁴/₆ = ²/₃. Ułamek ²/₃ jest ułamkiem nieskracalnym.

Wskazówka: Jeśli licznik i mianownik są liczbami parzystymi, to na pewno można je podzielić przez 2. Jeśli obie liczby kończą się na 0 lub 5, to na pewno można je podzielić przez 5.

Znaczenie Skracania Ułamków

Skracanie ułamków jest ważne, ponieważ:

• Upraszcza ułamki, ułatwiając dalsze obliczenia. Łatwiej operować na ułamkach z mniejszymi liczbami.
• Ułatwia porównywanie ułamków. Często łatwiej jest zauważyć, że dwa ułamki są równe, gdy są w postaci nieskracalnej.
• Daje przejrzysty wynik. W większości przypadków oczekuje się, że wynik obliczeń z ułamkami zostanie przedstawiony w postaci nieskracalnej.

Rozszerzanie Ułamków: Powiększanie Liczb

Rozszerzanie ułamków to proces powiększania licznika i mianownika ułamka, zachowując jednocześnie jego wartość. Robimy to, mnożąc licznik i mianownik przez tę samą liczbę różną od zera. Ta liczba nazywana jest czynnikiem rozszerzającym.

Jak Rozszerzać Ułamki? Krok po Kroku

1. Wybierz czynnik rozszerzający. Może to być dowolna liczba różna od zera.
2. Pomnóż licznik i mianownik przez ten czynnik. Otrzymasz nowy ułamek.

Przykład: Rozszerzmy ułamek ¹/₂ przez 3.

• Czynnikiem rozszerzającym jest 3.
• Mnożymy 1 przez 3 i otrzymujemy 3. Mnożymy 2 przez 3 i otrzymujemy 6.
• Otrzymujemy ułamek ³/₆.

Zatem, ¹/₂ = ³/₆. Pomimo że liczby w liczniku i mianowniku są inne, oba ułamki reprezentują tę samą wartość.

Znaczenie Rozszerzania Ułamków

Rozszerzanie ułamków jest ważne, ponieważ:

• Umożliwia porównywanie ułamków o różnych mianownikach. Aby porównać ułamki, często musimy doprowadzić je do wspólnego mianownika, a do tego potrzebujemy rozszerzania.
• Umożliwia dodawanie i odejmowanie ułamków o różnych mianownikach. Podobnie jak w przypadku porównywania, aby dodać lub odjąć ułamki, musimy najpierw znaleźć wspólny mianownik.
• Ułatwia rozwiązywanie zadań tekstowych. W wielu zadaniach tekstowych musimy przedstawić różne części całości za pomocą ułamków, a rozszerzanie pozwala nam dopasować te ułamki do odpowiednich jednostek.

Skracanie i Rozszerzanie Ułamków w Praktyce: Przykłady z Życia

Ułamki są obecne w naszym życiu codziennym na każdym kroku. Zobaczmy, jak skracanie i rozszerzanie ułamków może nam pomóc w różnych sytuacjach:

• Gotowanie: Przepis na ciasto wymaga ¹/₂ szklanki cukru. Chcesz upiec podwójną porcję ciasta. Musisz rozszerzyć ułamek ¹/₂ przez 2, aby dowiedzieć się, że potrzebujesz ²/₄ szklanki cukru, co jest równoważne 1 szklance.
• Dzielenie pizzy: Pizza jest podzielona na 8 kawałków. Zjadłeś 4 kawałki. Zjadłeś ⁴/₈ pizzy. Możesz skrócić ten ułamek do ¹/₂, co oznacza, że zjadłeś połowę pizzy.
• Mierzenie czasu: Spędzasz 15 minut na odrabianiu lekcji matematyki. Cała lekcja trwa 60 minut. Spędzasz ¹⁵/₆₀ lekcji na matematyce. Możesz skrócić ten ułamek do ¹/₄, co oznacza, że poświęcasz jedną czwartą lekcji na matematykę.
• Zakupy: Kupujesz produkt, który jest o ²⁵/₁₀₀ tańszy. Możesz skrócić ten ułamek do ¹/₄, co oznacza, że produkt jest o jedną czwartą tańszy.

Częste Błędy i Jak Ich Unikać

Podczas skracania i rozszerzania ułamków łatwo popełnić błędy. Oto kilka najczęstszych i jak ich unikać:

• Dzielenie lub mnożenie tylko licznika lub tylko mianownika. Pamiętaj, że zawsze musisz wykonać tę samą operację (dzielenie lub mnożenie) zarówno na liczniku, jak i na mianowniku, aby zachować wartość ułamka.
• Nie skracanie ułamka do końca. Zawsze sprawdzaj, czy ułamek można jeszcze skrócić.
• Używanie niepoprawnego czynnika rozszerzającego. Upewnij się, że mnożysz licznik i mianownik przez tę samą liczbę.
• Zapominanie o sprawdzeniu, czy mianownik jest równy zero. Pamiętaj, że mianownik nigdy nie może być równy zero.

Pamiętaj: Ćwiczenie czyni mistrza! Im więcej będziesz ćwiczyć skracanie i rozszerzanie ułamków, tym lepiej to zrozumiesz i tym łatwiej będzie Ci to robić.

Podsumowanie i Wezwanie do Działania

Skracanie i rozszerzanie ułamków to podstawowe, ale bardzo ważne umiejętności w matematyce. Pozwalają nam upraszczać ułamki, porównywać je, dodawać i odejmować, a także rozwiązywać zadania tekstowe. Pamiętaj, że skracanie to dzielenie licznika i mianownika przez wspólny dzielnik, a rozszerzanie to mnożenie licznika i mianownika przez czynnik rozszerzający.

Teraz, gdy już wiesz, jak skracać i rozszerzać ułamki, czas na praktykę! Znajdź w podręczniku zadania na skracanie i rozszerzanie ułamków i spróbuj je rozwiązać. Poproś rodziców lub nauczyciela o pomoc, jeśli masz problemy. Pamiętaj, że regularne ćwiczenia pomogą Ci opanować te umiejętności i poczuć się pewniej w świecie ułamków!

Powodzenia!