Siatka Graniastosłupa Pochyłego O Podstawie Prostokąta

Dobrze, przygotuję artykuł na temat siatki graniastosłupa pochyłego o podstawie prostokąta, starając się wyjaśnić to w prosty i przystępny sposób.

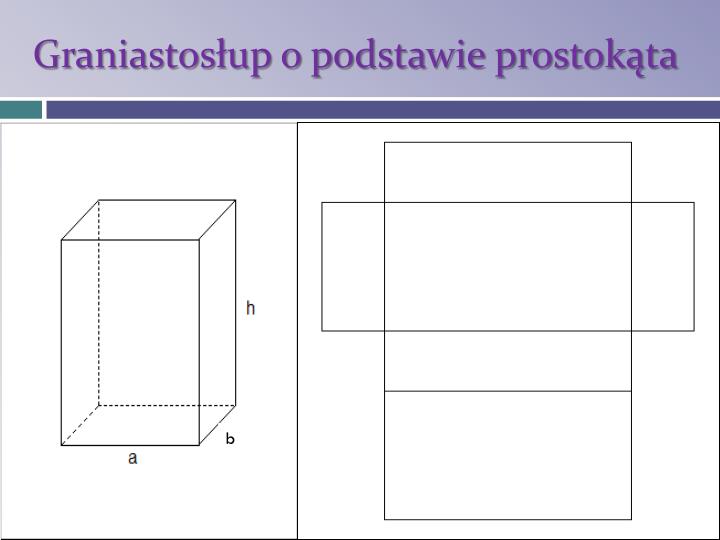
Zacznijmy od podstaw. Co to właściwie jest ten graniastosłup pochyły? Wyobraź sobie zwykły prostopadłościan, ale zamiast stać prosto, jest trochę "przechylony". To właśnie graniastosłup pochyły. Ważne jest, że nadal ma dwie podstawy, które są identycznymi prostokątami, ale ściany boczne nie są już prostokątami – są równoległobokami.

A siatka? Siatka to po prostu rozłożona figura przestrzenna na płasko. Wyobraź sobie, że rozcinasz kartonowe pudełko wzdłuż krawędzi i rozkładasz je, aby leżało płasko na stole. To właśnie jest siatka tego pudełka. Dla graniastosłupa pochyłego będzie to wyglądało trochę bardziej skomplikowanie niż dla zwykłego prostopadłościanu.

Jak zatem narysować siatkę graniastosłupa pochyłego o podstawie prostokąta? Potrzebujemy kilku informacji: wymiary prostokątnej podstawy (długość i szerokość) oraz długość krawędzi bocznych i kąt, pod jakim te krawędzie są nachylone do podstawy. Bez tych danych nie da się dokładnie narysować siatki. Załóżmy więc, że mamy te dane.

Najpierw rysujemy dwie identyczne podstawy, czyli dwa prostokąty. Rysujemy je tak, jakby leżały obok siebie na kartce. Te prostokąty są identyczne – mają takie same długości boków. Ważne jest, żeby były narysowane równolegle do siebie, bo w siatce będą połączone ścianami bocznymi.

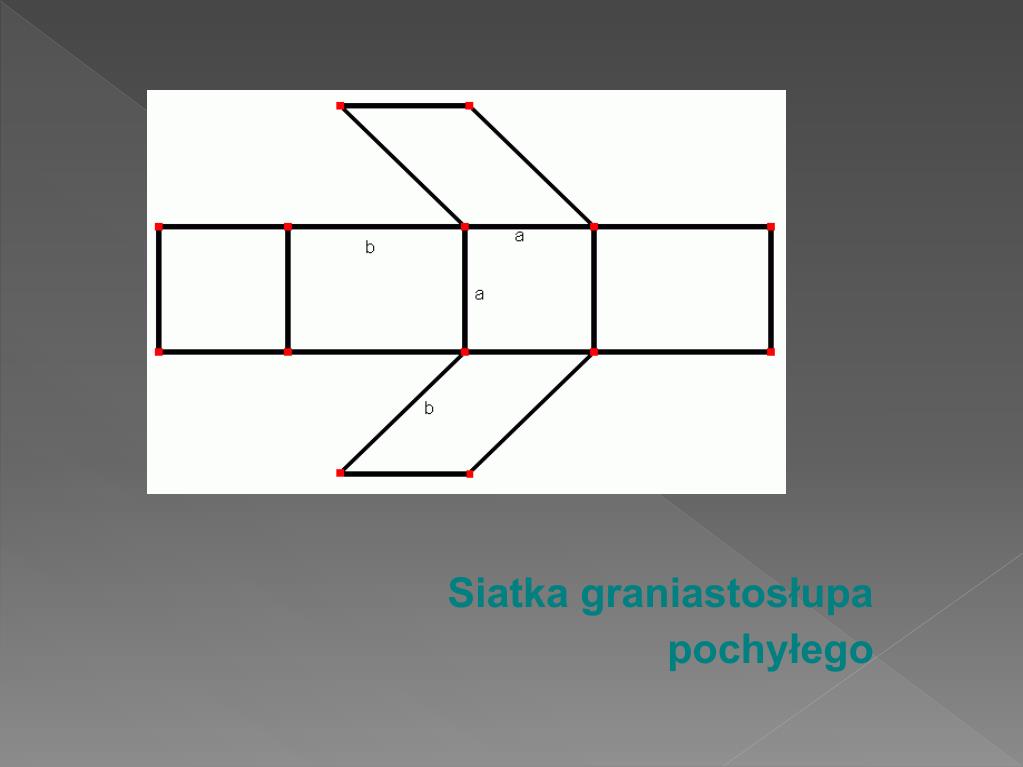
Następnie rysujemy ściany boczne. To tutaj zaczyna się robić trochę bardziej skomplikowanie, bo ściany boczne graniastosłupa pochyłego są równoległobokami, a nie prostokątami. Musimy znać długość krawędzi bocznej i kąt nachylenia.

Rysujemy pierwszy równoległobok. Jeden bok tego równoległoboku to bok podstawy, czyli jeden z boków prostokąta, który już narysowaliśmy. Drugi bok to krawędź boczna graniastosłupa. Kąt między tymi bokami jest istotny – to właśnie kąt nachylenia graniastosłupa. Musimy dokładnie odwzorować ten kąt, żeby siatka była prawidłowa. Równoległobok rysujemy "przyklejony" do jednej z podstaw, wzdłuż jednego z boków prostokąta.

Potem rysujemy drugi równoległobok. Robimy to podobnie, ale przyklejamy go do drugiego boku prostokąta podstawy. Ważne jest, aby krawędzie boczne równoległoboków miały tę samą długość i aby kąty nachylenia były takie same (lub odpowiednio symetryczne, w zależności od orientacji graniastosłupa).

Powtarzamy tę czynność dla pozostałych dwóch boków podstawy, rysując kolejne dwa równoległoboki. Każdy z tych równoległoboków "przyklejamy" do boku podstawy, aż wszystkie boki podstawy będą połączone ze ścianami bocznymi.

Na koniec dołączamy drugą podstawę (czyli drugi prostokąt) do jednej z krawędzi bocznych. Ważne jest, aby odpowiednio zorientować ten prostokąt, aby pasował do reszty siatki. Zazwyczaj przykleja się go do ostatniego narysowanego równoległoboku.

Teraz, jeśli wytniesz taką siatkę z papieru i spróbujesz ją złożyć, powinieneś otrzymać model graniastosłupa pochyłego o podstawie prostokąta.

Kilka ważnych wskazówek:

• Precyzja: Im dokładniej narysujesz prostokąty i równoległoboki, tym lepiej będzie wyglądał złożony model. Używaj linijki i kątomierza, aby uzyskać jak najlepsze wyniki.
• Orientacja: Upewnij się, że wszystkie równoległoboki są prawidłowo zorientowane względem podstaw. Chodzi o to, aby krawędzie, które mają się ze sobą połączyć podczas składania, miały tę samą długość.
• Wyobraźnia przestrzenna: Spróbuj wyobrazić sobie, jak siatka będzie się składać, zanim zaczniesz rysować. To pomoże Ci uniknąć błędów.

Uproszczony przykład

Wyobraźmy sobie, że mamy graniastosłup pochyły o podstawie prostokąta o wymiarach 5 cm x 3 cm. Długość krawędzi bocznej wynosi 6 cm, a kąt nachylenia wynosi 60 stopni.

1. Rysujemy dwa prostokąty o wymiarach 5 cm x 3 cm. Rysujemy je obok siebie, zachowując odstęp.
2. Do jednego z boków prostokąta (powiedzmy, tego o długości 5 cm) rysujemy równoległobok. Jeden bok równoległoboku to 5 cm (bok prostokąta), a drugi bok ma długość 6 cm. Kąt między tymi bokami to 60 stopni.
3. Do drugiego boku prostokąta (tego o długości 3 cm) rysujemy kolejny równoległobok. Jeden bok to 3 cm, drugi to 6 cm, a kąt nachylenia to 60 stopni.
4. Powtarzamy to dla pozostałych dwóch boków prostokąta, rysując kolejne dwa równoległoboki.
5. Na koniec, do jednego z równoległoboków "przyklejamy" drugi prostokąt (o wymiarach 5 cm x 3 cm).

To jest uproszczony opis. W rzeczywistości rysowanie z dokładnym kątem 60 stopni może wymagać użycia kątomierza i precyzyjnych narzędzi.

Dodatkowe uwagi

Rysowanie siatki graniastosłupa pochyłego może być trudne, zwłaszcza jeśli nie jesteś przyzwyczajony do rysowania figur przestrzennych. Najważniejsze to zrozumieć, jak poszczególne ściany łączą się ze sobą i jak kąt nachylenia wpływa na kształt równoległoboków.

Możesz zacząć od prostszych przykładów, z mniejszymi kątami nachylenia, a następnie stopniowo przechodzić do bardziej skomplikowanych przypadków. Możesz również poszukać w Internecie przykładów siatek graniastosłupów pochyłych, aby zobaczyć, jak wyglądają i jak są narysowane.

Pamiętaj, że praktyka czyni mistrza. Im więcej będziesz rysować siatek graniastosłupów pochyłych, tym łatwiej Ci to będzie przychodziło. Nie zrażaj się, jeśli początki będą trudne. Poświęć trochę czasu na zrozumienie zasad i poeksperymentuj z różnymi wymiarami i kątami nachylenia.

I co najważniejsze – baw się dobrze! Rysowanie siatek figur przestrzennych to świetny sposób na rozwijanie wyobraźni przestrzennej i umiejętności matematycznych. Mam nadzieję, że ten artykuł pomógł Ci zrozumieć, jak narysować siatkę graniastosłupa pochyłego o podstawie prostokąta. Powodzenia!