Siatka Graniastosłupa O Podstawie Trójkata

Czy kiedykolwiek zastanawiałeś się, jak matematyka przenika się z naszym codziennym życiem, nawet w tak pozornie prostych przedmiotach jak pudełka prezentowe, zabawki dla dzieci, czy elementy architektury? Często nie zdajemy sobie sprawy, że za ich kształtem kryją się prawa geometrii, a jednym z fascynujących przykładów jest siatka graniastosłupa o podstawie trójkąta. Zrozumienie tego pojęcia może wydawać się trudne, ale obiecuję, że razem rozwiejemy wszelkie wątpliwości i pokażemy, jak przydatna jest ta wiedza.

Wyobraź sobie, że masz przed sobą kartonowy graniastosłup trójkątny – może to być opakowanie na kredki trójkątne, albo dach miniaturowego domku dla lalek. Teraz spróbuj go rozłożyć na płasko, tak aby powstała jedna, spójna figura. To, co otrzymasz, to właśnie siatka graniastosłupa. Ale dlaczego mielibyśmy w ogóle się tym zajmować? Przekonajmy się.

Dlaczego warto zrozumieć siatkę graniastosłupa trójkątnego?

Zrozumienie siatki graniastosłupa trójkątnego ma ogromne znaczenie w wielu dziedzinach:

Edukacja: Pomaga w wizualizacji figur przestrzennych i zrozumieniu relacji między dwuwymiarowymi i trójwymiarowymi obiektami. To świetny sposób na rozwój wyobraźni przestrzennej u dzieci i młodzieży.
Projektowanie i Architektura: Architekci i projektanci wykorzystują siatki do projektowania budynków, opakowań, mebli i innych trójwymiarowych obiektów. Pozwala to na dokładne planowanie i minimalizację odpadów materiałowych.
Rzemiosło i Hobby: Osoby zajmujące się rękodziełem, modelarstwem czy origami mogą wykorzystać wiedzę o siatkach do tworzenia precyzyjnych i skomplikowanych konstrukcji.
Przemysł opakowaniowy: Firmy produkujące opakowania wykorzystują siatki do projektowania efektywnych i ekonomicznych pudełek i pojemników. Optymalizacja siatki pozwala na zmniejszenie zużycia materiałów i kosztów produkcji.

W skrócie, zrozumienie siatki graniastosłupa trójkątnego to umiejętność, która może być przydatna w wielu aspektach życia, od praktycznych zastosowań zawodowych po kreatywne hobby.

Co to jest siatka graniastosłupa trójkątnego?

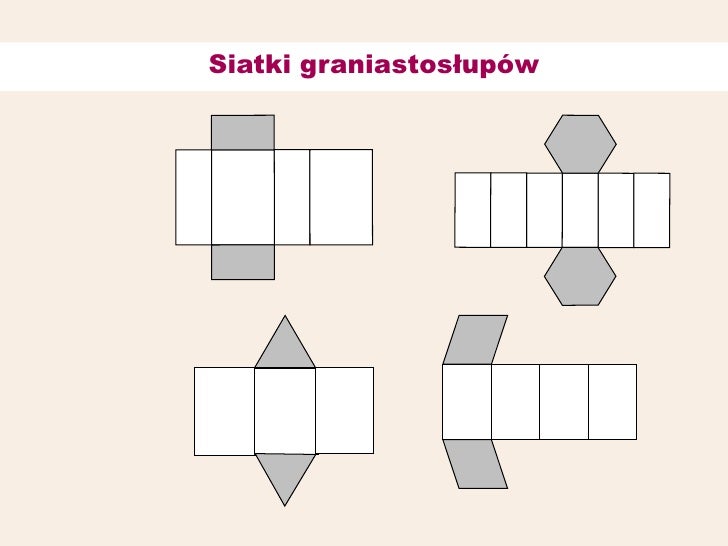
Siatka graniastosłupa trójkątnego to płaski wzór, który po złożeniu tworzy graniastosłup o podstawie trójkąta. Składa się ona z dwóch trójkątów (podstawy) i trzech prostokątów (ściany boczne). Ważne jest, aby odpowiednio połączyć te elementy, aby powstał zamknięty kształt.

Elementy siatki:

Dwie podstawy (trójkąty): Muszą być identyczne. Mogą to być trójkąty równoboczne, równoramienne lub różnoboczne.
Trzy ściany boczne (prostokąty): Wysokość każdego prostokąta jest równa wysokości graniastosłupa. Szerokość każdego prostokąta odpowiada długości odpowiedniego boku trójkąta w podstawie.

Kluczowe jest, aby długość boków prostokątów odpowiadała długościom boków trójkąta w podstawie, a ich szerokość była równa wysokości graniastosłupa. Inaczej, po złożeniu, siatka nie utworzy prawidłowego graniastosłupa.

Jak narysować siatkę graniastosłupa trójkątnego?

Rysowanie siatki graniastosłupa trójkątnego może wydawać się skomplikowane, ale z odpowiednim podejściem staje się proste. Oto krok po kroku:

Narysuj trójkąt podstawy: Zdecyduj, jaki ma być kształt trójkąta (równoboczny, równoramienny, różnoboczny) i narysuj go. Pamiętaj, że będziesz potrzebował dwóch identycznych trójkątów.
Określ wysokość graniastosłupa: To będzie szerokość prostokątów.
Narysuj prostokąty: Narysuj trzy prostokąty. Długość każdego prostokąta musi odpowiadać długości jednego z boków trójkąta. Szerokość prostokątów musi być równa wcześniej ustalonej wysokości graniastosłupa.
Połącz elementy: Umieść trójkąty po obu stronach prostokątów, tak aby boki trójkątów pasowały do odpowiednich boków prostokątów. Upewnij się, że masz możliwość złożenia siatki i sklejenia jej w graniastosłup.

Pamiętaj, że istnieje kilka sposobów na rozmieszczenie prostokątów i trójkątów, ale ważne jest, aby zachować odpowiednie proporcje i kolejność.

Różne rodzaje trójkątów w podstawie:

Trójkąt równoboczny: Wszystkie boki mają równe długości, więc wszystkie prostokąty będą identyczne.
Trójkąt równoramienny: Dwa boki mają równe długości, więc dwa prostokąty będą identyczne.
Trójkąt różnoboczny: Wszystkie boki mają różne długości, więc wszystkie prostokąty będą miały różne wymiary.

Przykładowe zadania i ćwiczenia

Aby lepiej zrozumieć siatkę graniastosłupa trójkątnego, warto rozwiązać kilka zadań:

Zadanie 1: Narysuj siatkę graniastosłupa o podstawie trójkąta równobocznego o boku 5 cm i wysokości 8 cm. Oblicz pole powierzchni całkowitej graniastosłupa.
Zadanie 2: Czy z podanej siatki można złożyć graniastosłup trójkątny? Uzasadnij odpowiedź. (Pokaż rysunek siatki).
Zadanie 3: Zaprojektuj pudełko w kształcie graniastosłupa trójkątnego na prezent. Określ wymiary pudełka i narysuj jego siatkę.

Rozwiązywanie takich zadań pomaga utrwalić wiedzę i zrozumieć praktyczne zastosowanie siatki graniastosłupa trójkątnego.

Krytyczne spojrzenie: Ograniczenia i alternatywy

Choć koncepcja siatki graniastosłupa trójkątnego jest użyteczna, ma pewne ograniczenia. Przede wszystkim, tworzenie idealnie dokładnych siatek wymaga precyzyjnych pomiarów i rysunków. W rzeczywistości, podczas produkcji opakowań, często stosuje się uproszczenia i kompromisy, aby zoptymalizować koszty i proces produkcyjny.

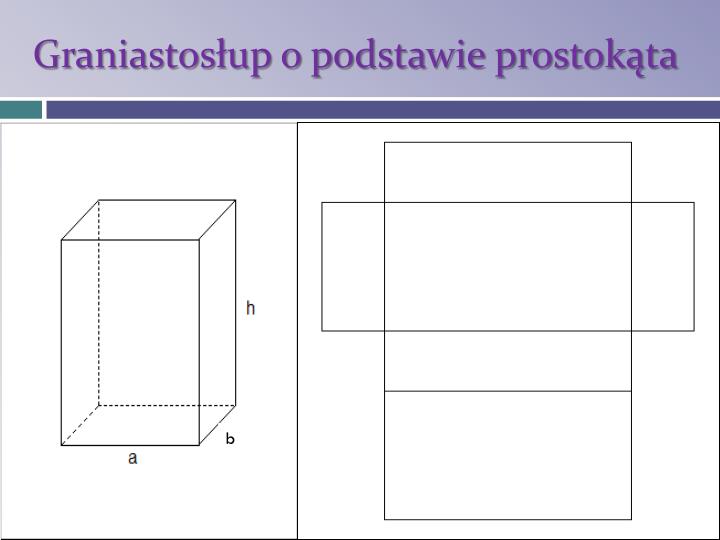
Ponadto, w niektórych przypadkach, inne rodzaje graniastosłupów (np. graniastosłupy czworokątne) mogą być bardziej efektywne i praktyczne w zastosowaniu. Wybór odpowiedniego kształtu zależy od konkretnych potrzeb i wymagań projektowych.

Niektórzy mogą argumentować, że w dobie programów do projektowania 3D, rysowanie siatek ręcznie jest przestarzałe. To prawda, że programy te znacznie ułatwiają proces projektowania, ale zrozumienie podstawowych zasad geometrii i siatek jest nadal kluczowe dla efektywnego korzystania z tych narzędzi.

Praktyczne wskazówki i triki

Oto kilka praktycznych wskazówek, które mogą ułatwić pracę z siatką graniastosłupa trójkątnego:

Użyj linijki i kątomierza: Do precyzyjnego rysowania siatki użyj linijki i kątomierza. To zapewni dokładność i unikniesz błędów.
Wykorzystaj papier w kratkę: Papier w kratkę ułatwia rysowanie prostych i równych linii.
Zrób model z papieru: Po narysowaniu siatki, wytnij ją i złóż, aby sprawdzić, czy wszystko pasuje. To pozwoli na wczesne wykrycie ewentualnych błędów.
Eksperymentuj z różnymi rodzajami trójkątów: Spróbuj narysować siatki dla różnych rodzajów trójkątów (równobocznych, równoramiennych, różnobocznych). To pomoże zrozumieć, jak kształt trójkąta wpływa na wygląd siatki.

Pamiętaj, że praktyka czyni mistrza. Im więcej siatek narysujesz, tym łatwiej będzie Ci to przychodziło.

Siatka graniastosłupa trójkątnego w programach graficznych

W dzisiejszych czasach, projektowanie siatek graniastosłupów trójkątnych często odbywa się za pomocą programów graficznych, takich jak AutoCAD, SketchUp, czy Blender. Te programy oferują wiele narzędzi i funkcji, które ułatwiają tworzenie precyzyjnych i skomplikowanych siatek. Pozwalają one na:

Automatyczne generowanie siatek: Programy mogą automatycznie generować siatki na podstawie zadanych parametrów.
Wizualizację 3D: Możliwość podglądu gotowego graniastosłupa w 3D przed wydrukowaniem siatki.
Optymalizację siatek: Narzędzia do optymalizacji siatek w celu minimalizacji zużycia materiałów.
Współpracę zespołową: Umożliwiają łatwą współpracę w zespole projektowym.

Nauka obsługi tych programów jest bardzo wartościowa dla każdego, kto zajmuje się projektowaniem i modelowaniem 3D.

Podsumowanie i co dalej?

Zrozumienie siatki graniastosłupa trójkątnego to ważny krok w nauce geometrii i wizualizacji przestrzennej. Wiedza ta może być przydatna w wielu dziedzinach, od edukacji po projektowanie i rzemiosło. Mimo pewnych ograniczeń, koncepcja siatki pozostaje cennym narzędziem w zrozumieniu relacji między dwuwymiarowymi i trójwymiarowymi obiektami.

Teraz, gdy już wiesz, czym jest siatka graniastosłupa trójkątnego, spróbuj samodzielnie narysować kilka siatek. Eksperymentuj z różnymi rodzajami trójkątów i wymiarami graniastosłupów. Spróbuj zaprojektować własne pudełko w kształcie graniastosłupa trójkątnego. A może zastanów się, gdzie w Twoim otoczeniu możesz znaleźć przedmioty oparte na tej konstrukcji?

Czy dostrzegasz teraz więcej możliwości, w których wiedza o siatkach graniastosłupów może Ci się przydać?