Ruch Jednostajny Po Okręgu Wzory

Czy kiedykolwiek zastanawiałeś się, jak obliczyć prędkość karuzeli, albo jak przewidzieć, gdzie znajdzie się wskazówka zegara za kilka sekund? Ruch jednostajny po okręgu to temat, który, choć może wydawać się skomplikowany, otacza nas każdego dnia. Zrozumienie jego zasad pozwala nam opisać ruch wielu obiektów, od planet krążących wokół Słońca, po wirujące bębny pralek. Ten artykuł ma na celu przybliżyć Ci ten fascynujący temat w przystępny i praktyczny sposób.

Wprowadzenie do Ruchu Jednostajnego po Okręgu

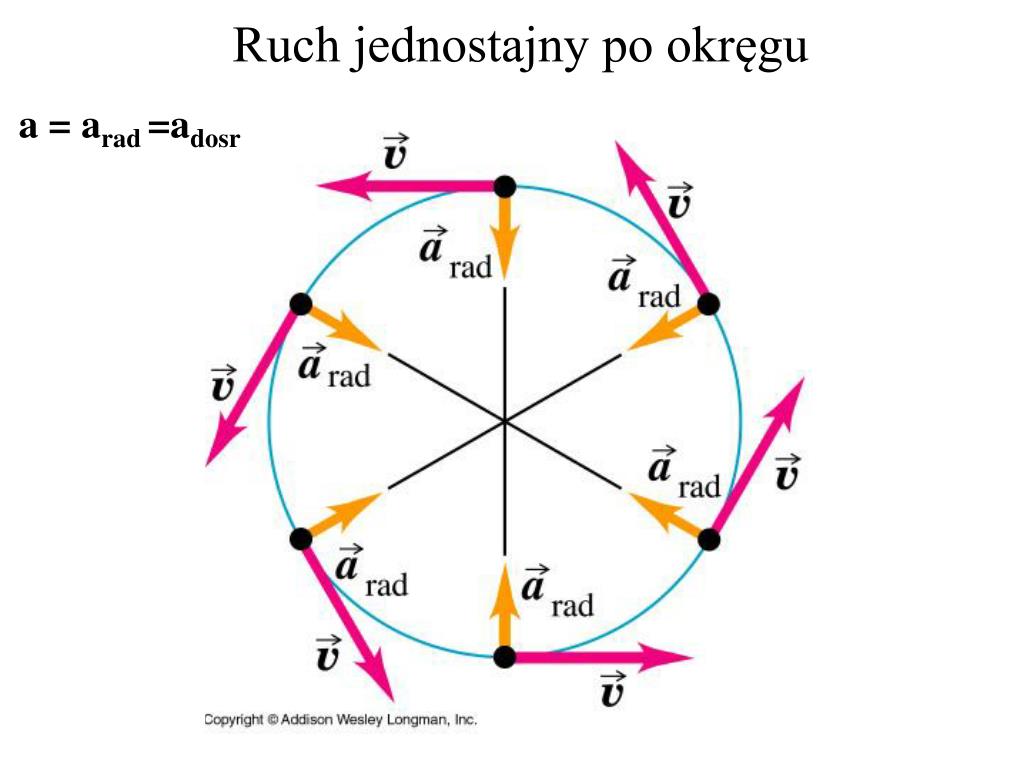
Ruch jednostajny po okręgu to taki ruch, w którym ciało porusza się po okręgu ze stałą wartością prędkości. Kluczowe jest tutaj słowo "wartość", ponieważ kierunek prędkości wciąż się zmienia, co oznacza, że występuje przyspieszenie, mimo stałej "szybkości".

Podstawowe Pojęcia

Zanim przejdziemy do wzorów, warto uporządkować podstawowe pojęcia:

Promień (r): Odległość od środka okręgu do punktu, po którym porusza się ciało.
Okres (T): Czas potrzebny na wykonanie jednego pełnego okrążenia. Mierzony w sekundach (s).
Częstotliwość (f): Liczba okrążeń wykonanych w jednostce czasu (zazwyczaj w sekundę). Mierzona w hercach (Hz), gdzie 1 Hz = 1 okrążenie na sekundę. Związek między okresem i częstotliwością to: f = 1/T.
Prędkość liniowa (v): Wartość prędkości, z jaką porusza się ciało po okręgu. Mierzona w metrach na sekundę (m/s).
Prędkość kątowa (ω): Szybkość zmiany kąta, wyrażona w radianach na sekundę (rad/s).
Przyspieszenie dośrodkowe (a_r): Przyspieszenie skierowane do środka okręgu, powodujące zmianę kierunku prędkości. Mierzone w metrach na sekundę kwadrat (m/s²).

Kluczowe Wzory Ruchu Jednostajnego po Okręgu

Teraz przejdźmy do wzorów, które pozwolą nam opisać i obliczyć parametry ruchu jednostajnego po okręgu.

Prędkość Liniowa (v)

Prędkość liniową możemy obliczyć na dwa sposoby. Pierwszy sposób, korzystający z okresu (T) i promienia (r), wygląda następująco:

v = 2πr / T

Gdzie 2πr to obwód okręgu, a T to czas potrzebny na jego pokonanie. Drugi sposób, wykorzystujący prędkość kątową (ω) i promień (r), jest równie prosty:

v = ωr

Pamiętaj! Prędkość liniowa jest zawsze styczna do okręgu w danym punkcie.

Prędkość Kątowa (ω)

Prędkość kątową możemy obliczyć, korzystając z okresu (T) lub częstotliwości (f):

ω = 2π / T lub ω = 2πf

Prędkość kątowa mówi nam, o jaki kąt (w radianach) obraca się ciało w ciągu sekundy.

Przyspieszenie Dośrodkowe (a_r)

Przyspieszenie dośrodkowe, jak wspomniano, jest skierowane do środka okręgu i powoduje zmianę kierunku prędkości. Możemy je obliczyć na dwa sposoby:

a_r = v² / r lub a_r = ω²r

Zauważ, że im większa prędkość liniowa lub kątowa, a im mniejszy promień okręgu, tym większe przyspieszenie dośrodkowe.

Przykłady i Zastosowania

Ruch jednostajny po okręgu jest obecny w wielu aspektach naszego życia. Oto kilka przykładów:

Ruch Ziemi wokół Słońca: Chociaż orbita Ziemi nie jest idealnym okręgiem i prędkość Ziemi zmienia się w ciągu roku, model ruchu jednostajnego po okręgu jest dobrym przybliżeniem.
Kręcąca się karuzela: Dzieci siedzące na karuzeli poruszają się ruchem jednostajnym po okręgu (w przybliżeniu).
Wirujący dysk twardy: Głowica dysku twardego porusza się nad wirującymi talerzami.
Wskazówki zegara: Ruch wskazówek zegara (sekundnika, minutnika, godzinowej) jest przykładem ruchu jednostajnego po okręgu.

Przykład Obliczeniowy

Załóżmy, że mamy karuzelę o promieniu 5 metrów, która wykonuje jeden obrót w ciągu 10 sekund. Oblicz prędkość liniową dziecka siedzącego na tej karuzeli.

Mamy dane: r = 5 m, T = 10 s

Korzystamy ze wzoru: v = 2πr / T

v = 2 * 3.14 * 5 m / 10 s

v = 3.14 m/s

Dziecko porusza się z prędkością około 3.14 m/s.

Praktyczne Wskazówki

Zrozumienie ruchu jednostajnego po okręgu może być łatwiejsze, jeśli zastosujesz się do kilku prostych wskazówek:

Rysuj schematy: Narysuj okrąg i oznacz promień, prędkość liniową i przyspieszenie dośrodkowe. To pomoże Ci wizualizować problem.
Zwracaj uwagę na jednostki: Upewnij się, że wszystkie jednostki są zgodne (np. promień w metrach, czas w sekundach).
Sprawdzaj swoje wyniki: Zastanów się, czy uzyskany wynik ma sens. Czy prędkość karuzeli jest realistyczna?
Korzystaj z interaktywnych symulacji: W Internecie znajdziesz wiele symulacji ruchu jednostajnego po okręgu, które pozwolą Ci eksperymentować i lepiej zrozumieć ten temat.

Podsumowanie

Ruch jednostajny po okręgu, choć z pozoru skomplikowany, jest fundamentalnym zagadnieniem fizyki, które pozwala nam opisywać wiele zjawisk w naszym otoczeniu. Znajomość wzorów na prędkość liniową, prędkość kątową i przyspieszenie dośrodkowe oraz umiejętność ich stosowania, to klucz do zrozumienia tego typu ruchu. Pamiętaj, praktyka czyni mistrza! Rozwiązuj zadania, analizuj przykłady i eksperymentuj, a ruch jednostajny po okręgu przestanie być dla Ciebie tajemnicą.

Mamy nadzieję, że ten artykuł pomógł Ci zrozumieć zasady rządzące ruchem jednostajnym po okręgu. Jeśli masz jakiekolwiek pytania, nie wahaj się ich zadać! Powodzenia w dalszej nauce!