Ruch Jednostajnie Zmienny Wykresy

Czy kiedykolwiek zastanawiałeś się, jak obliczyć, ile czasu zajmie Ci dogonienie autobusu, który właśnie ruszył z przystanku? A może jak wysoko wzniesie się piłka podrzucona w górę? Odpowiedzi na te pytania, i wiele innych związanych z ruchem, kryją się w zrozumieniu ruchu jednostajnie zmiennego. Wiele osób uważa fizykę za trudną, ale postaramy się pokazać, że zrozumienie podstawowych zasad, takich jak ruch jednostajnie zmienny, może być nie tylko łatwe, ale i fascynujące.

Czym jest ruch jednostajnie zmienny?

Wyobraź sobie samochód, który przyspiesza lub hamuje z równomierną zmianą prędkości. Właśnie to jest ruch jednostajnie zmienny. To taki ruch, w którym prędkość ciała zmienia się w sposób jednakowy w jednostce czasu. Innymi słowy, przyspieszenie (lub opóźnienie) jest stałe. Kluczowe słowo to "jednostajnie" – zmiana prędkości jest przewidywalna i regularna.

Możemy rozróżnić dwa główne typy ruchu jednostajnie zmiennego:

• Ruch jednostajnie przyspieszony: Prędkość ciała rośnie w czasie. Przykład: Samochód ruszający z miejsca.
• Ruch jednostajnie opóźniony: Prędkość ciała maleje w czasie. Przykład: Samochód hamujący przed światłami.

Różnica między ruchem jednostajnym a jednostajnie zmiennym

Warto odróżnić ruch jednostajnie zmienny od ruchu jednostajnego. W ruchu jednostajnym prędkość jest stała – ciało porusza się z niezmienną szybkością w jednym kierunku. W ruchu jednostajnie zmiennym, jak już wiemy, prędkość się zmienia. Dlatego w opisie ruchu jednostajnie zmiennego musimy brać pod uwagę, poza prędkością, również przyspieszenie (lub opóźnienie).

Kluczowe wzory w ruchu jednostajnie zmiennym

Aby opisać ruch jednostajnie zmienny, używamy kilku podstawowych wzorów. Zrozumienie tych wzorów pozwoli Ci rozwiązywać zadania i przewidywać, jak zachowa się ciało w ruchu.

• Prędkość w funkcji czasu: v = v₀ + at
  Gdzie:
  • v - prędkość końcowa
  • v₀ - prędkość początkowa
  • a - przyspieszenie (jeśli ruch jest opóźniony, 'a' jest ujemne)
  • t - czas
• Droga w funkcji czasu: s = v₀t + (1/2)at²
  Gdzie:
  • s - przebyta droga
  • v₀ - prędkość początkowa
  • a - przyspieszenie (jeśli ruch jest opóźniony, 'a' jest ujemne)
  • t - czas
• Związek prędkości z drogą: v² = v₀² + 2as
  Gdzie:
  • v - prędkość końcowa
  • v₀ - prędkość początkowa
  • a - przyspieszenie (jeśli ruch jest opóźniony, 'a' jest ujemne)
  • s - przebyta droga

Te wzory, choć na pierwszy rzut oka mogą wydawać się skomplikowane, są narzędziami, które pozwalają nam dokładnie opisać ruch jednostajnie zmienny. Ważne jest, aby zrozumieć, co oznaczają poszczególne symbole i jak je stosować w praktyce.

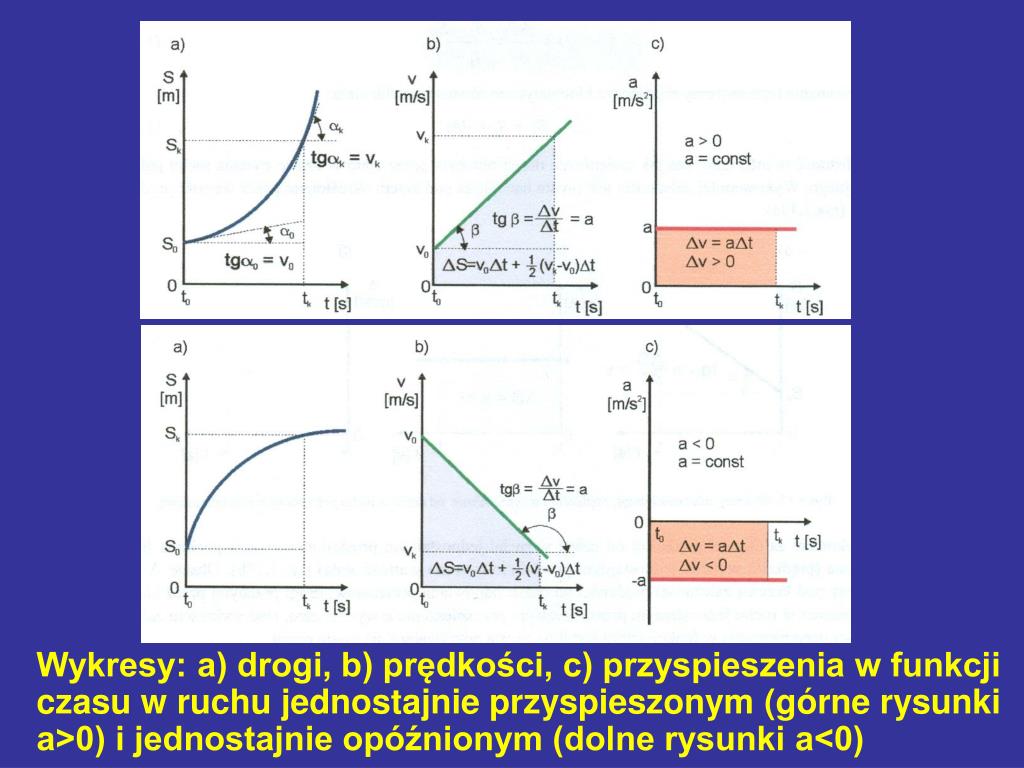
Wykresy w ruchu jednostajnie zmiennym

Wykresy to potężne narzędzie do wizualizacji ruchu. Pozwalają one na szybką analizę i zrozumienie zależności między różnymi wielkościami fizycznymi.

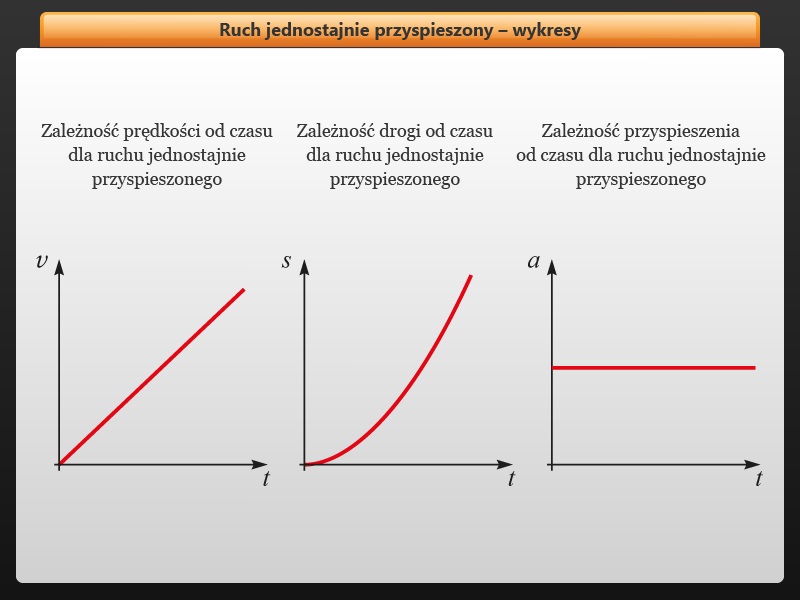
Wykres prędkości od czasu (v(t))

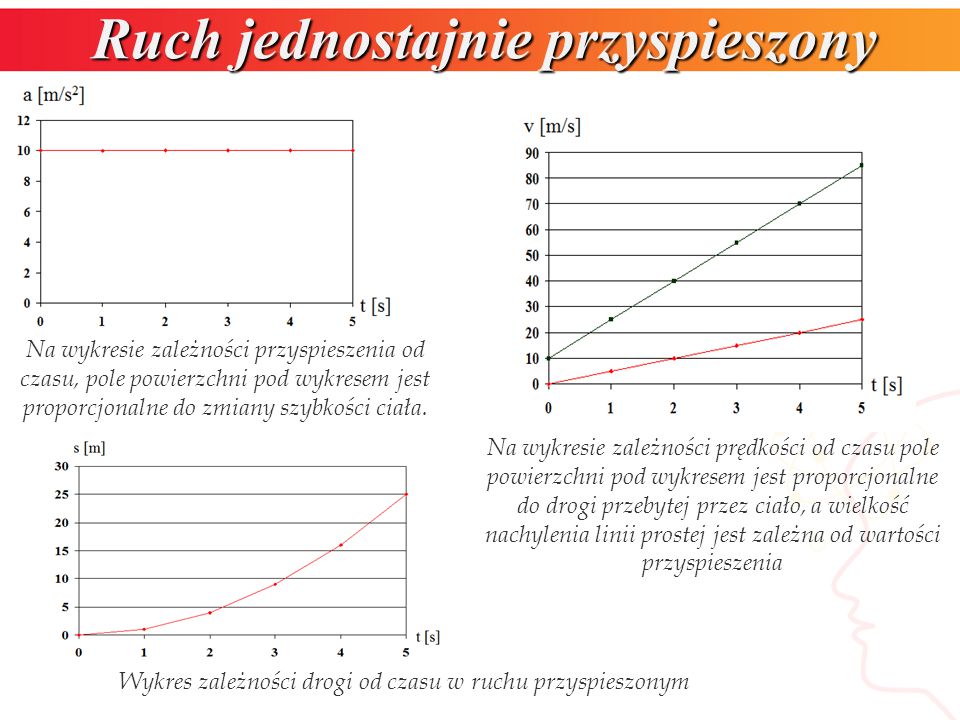
Wykres v(t) w ruchu jednostajnie zmiennym jest linią prostą. Nachylenie tej prostej odpowiada przyspieszeniu (lub opóźnieniu). Jeśli linia wznosi się, mamy do czynienia z ruchem przyspieszonym (przyspieszenie jest dodatnie). Jeśli linia opada, mamy do czynienia z ruchem opóźnionym (przyspieszenie jest ujemne). Pozioma linia oznacza brak zmiany prędkości, czyli ruch jednostajny.

Pole pod wykresem v(t) odpowiada przebytej drodze w danym przedziale czasu. Można to wykorzystać do obliczania drogi nawet w bardziej skomplikowanych sytuacjach.

Wykres drogi od czasu (s(t))

Wykres s(t) w ruchu jednostajnie zmiennym jest parabolą. Kształt paraboli zależy od wartości przyspieszenia. Jeśli przyspieszenie jest dodatnie (ruch przyspieszony), parabola otwiera się "do góry". Jeśli przyspieszenie jest ujemne (ruch opóźniony), parabola otwiera się "do dołu".

Nachylenie stycznej do wykresu s(t) w danym punkcie odpowiada prędkości chwilowej w tym momencie czasu. To znaczy, im bardziej stroma styczna, tym większa prędkość.

Wykres przyspieszenia od czasu (a(t))

Wykres a(t) w ruchu jednostajnie zmiennym jest linią poziomą. Ponieważ przyspieszenie jest stałe, wykres przyjmuje postać poziomej linii na wysokości wartości tego przyspieszenia. Jeśli przyspieszenie jest równe zero, linia pokrywa się z osią czasu, co oznacza brak przyspieszenia, a więc ruch jednostajny.

Praktyczne zastosowania ruchu jednostajnie zmiennego

Ruch jednostajnie zmienny opisuje wiele sytuacji z życia codziennego. Oto kilka przykładów:

• Spadanie swobodne: Ciało spadające pod wpływem grawitacji (pomijając opór powietrza) porusza się ruchem jednostajnie przyspieszonym. Przyspieszenie ziemskie (g ≈ 9.81 m/s²) jest stałe, więc prędkość spadającego ciała rośnie w sposób jednostajny.
• Hamowanie samochodu: Podczas hamowania, samochód zwalnia, poruszając się ruchem jednostajnie opóźnionym (zakładając, że siła hamowania jest stała). Zrozumienie tego ruchu jest kluczowe dla bezpieczeństwa na drodze.
• Rzut pionowy: Piłka rzucona pionowo w górę najpierw zwalnia (ruch jednostajnie opóźniony), a następnie przyspiesza w dół (ruch jednostajnie przyspieszony). Analiza tego ruchu pozwala obliczyć wysokość, na jaką wzniesie się piłka i czas jej lotu.
• Ruch windy: Podczas ruszania i zatrzymywania, winda porusza się ruchem jednostajnie zmiennym. W środkowej fazie, gdy winda porusza się ze stałą prędkością, mamy do czynienia z ruchem jednostajnym.

Zrozumienie zasad ruchu jednostajnie zmiennego pozwala nam lepiej rozumieć świat wokół nas i przewidywać zachowanie się ciał w ruchu. To wiedza, która ma zastosowanie w wielu dziedzinach, od sportu po inżynierię.

Podsumowanie i praktyczne porady

Ruch jednostajnie zmienny to fundamentalne pojęcie w fizyce, opisujące ruch, w którym prędkość zmienia się w sposób jednostajny. Zrozumienie wzorów, wykresów i przykładów z życia codziennego pozwala na efektywne rozwiązywanie zadań i przewidywanie zachowania się ciał w ruchu.

Kilka praktycznych porad:

• Zacznij od zrozumienia definicji: Upewnij się, że rozumiesz, co to jest ruch jednostajnie zmienny i czym różni się od ruchu jednostajnego.
• Opanuj wzory: Zapamiętaj wzory na prędkość, drogę i związek prędkości z drogą. Wypisz je na kartce i miej je pod ręką podczas rozwiązywania zadań.
• Analizuj wykresy: Zrozum, jak wyglądają wykresy v(t), s(t) i a(t) dla ruchu jednostajnie zmiennego. Naucz się odczytywać z nich informacje o ruchu.
• Rozwiązuj zadania: Ćwicz rozwiązywanie zadań, zaczynając od prostych przykładów, a następnie przechodząc do bardziej skomplikowanych.
• Szukaj przykładów w życiu codziennym: Zwracaj uwagę na przykłady ruchu jednostajnie zmiennego w otaczającym Cię świecie. To pomoże Ci lepiej zrozumieć to pojęcie i zapamiętać wzory.

Pamiętaj, że fizyka nie musi być trudna. Z odrobiną wysiłku i zrozumienia podstawowych zasad, możesz z łatwością opanować ruch jednostajnie zmienny i wiele innych zagadnień fizycznych. Powodzenia!