Ruch Jednostajnie Przyspieszony I Opóźniony Zadania

Ruch jednostajnie przyspieszony i opóźniony to fundamentalne pojęcia w fizyce, opisujące zmiany prędkości ciał w czasie. Zrozumienie tych zagadnień jest kluczowe do dalszej nauki mechaniki i dynamiki. Poniżej znajdziesz przykłady zadań wraz z rozwiązaniami, które pomogą Ci opanować tę tematykę.

Zacznijmy od definicji. Ruch jednostajnie przyspieszony charakteryzuje się stałym przyspieszeniem, co oznacza, że prędkość ciała rośnie liniowo w czasie. Ruch jednostajnie opóźniony natomiast ma stałe opóźnienie (ujemne przyspieszenie), co powoduje liniowy spadek prędkości.

Zadanie 1: Rowerzysta

Rowerzysta rusza z miejsca i przyspiesza jednostajnie przez 10 sekund, osiągając prędkość 20 m/s. Oblicz przyspieszenie rowerzysty oraz drogę, jaką pokonał w tym czasie.

Rozwiązanie:

Mamy dane:

• Czas (t) = 10 s
• Prędkość końcowa (v) = 20 m/s
• Prędkość początkowa (v0) = 0 m/s (ponieważ rowerzysta rusza z miejsca)

Szukane:

• Przyspieszenie (a)
• Droga (s)

Użyjemy wzoru na przyspieszenie: a = (v - v0) / t a = (20 m/s - 0 m/s) / 10 s = 2 m/s²

Teraz obliczymy drogę. Możemy użyć wzoru: s = v0 * t + (1/2) * a * t² s = 0 * 10 s + (1/2) * 2 m/s² * (10 s)² = 100 m

Odpowiedź: Przyspieszenie rowerzysty wynosi 2 m/s², a pokonana droga to 100 m.

Zadanie 2: Samochód Hamujący

Samochód jadący z prędkością 30 m/s zaczyna hamować ze stałym opóźnieniem 5 m/s². Oblicz czas, po którym samochód się zatrzyma oraz drogę hamowania.

Rozwiązanie:

Dane:

• Prędkość początkowa (v0) = 30 m/s
• Przyspieszenie (a) = -5 m/s² (opóźnienie, więc wartość ujemna)
• Prędkość końcowa (v) = 0 m/s (samochód się zatrzymuje)

Szukane:

• Czas (t)
• Droga (s)

Użyjemy wzoru na przyspieszenie: a = (v - v0) / t, przekształcając go, aby obliczyć czas: t = (v - v0) / a t = (0 m/s - 30 m/s) / (-5 m/s²) = 6 s

Teraz obliczymy drogę hamowania. Możemy użyć wzoru: s = v0 * t + (1/2) * a * t² s = 30 m/s * 6 s + (1/2) * (-5 m/s²) * (6 s)² = 180 m - 90 m = 90 m

Odpowiedź: Samochód zatrzyma się po 6 sekundach, a droga hamowania wynosi 90 m.

Zadanie 3: Spadający Kamień

Kamień spada swobodnie z wysokości 20 m. Pomijając opór powietrza, oblicz czas spadania kamienia oraz jego prędkość tuż przed uderzeniem o ziemię (przyjmij przyspieszenie ziemskie g = 9.81 m/s²).

Rozwiązanie:

Dane:

• Wysokość (s) = 20 m
• Przyspieszenie (a) = g = 9.81 m/s²
• Prędkość początkowa (v0) = 0 m/s (kamień spada swobodnie)

Szukane:

• Czas (t)
• Prędkość końcowa (v)

Użyjemy wzoru na drogę w ruchu jednostajnie przyspieszonym: s = v0 * t + (1/2) * a * t², co upraszcza się do: s = (1/2) * g * t² Przekształcamy wzór, aby obliczyć czas: t² = (2 * s) / g => t = √((2 * s) / g) t = √((2 * 20 m) / 9.81 m/s²) = √(40 / 9.81) s = √4.077 s ≈ 2.02 s

Teraz obliczymy prędkość końcową. Możemy użyć wzoru: v = v0 + a * t v = 0 m/s + 9.81 m/s² * 2.02 s = 19.82 m/s

Odpowiedź: Kamień spada przez około 2.02 sekundy, a jego prędkość tuż przed uderzeniem o ziemię wynosi około 19.82 m/s.

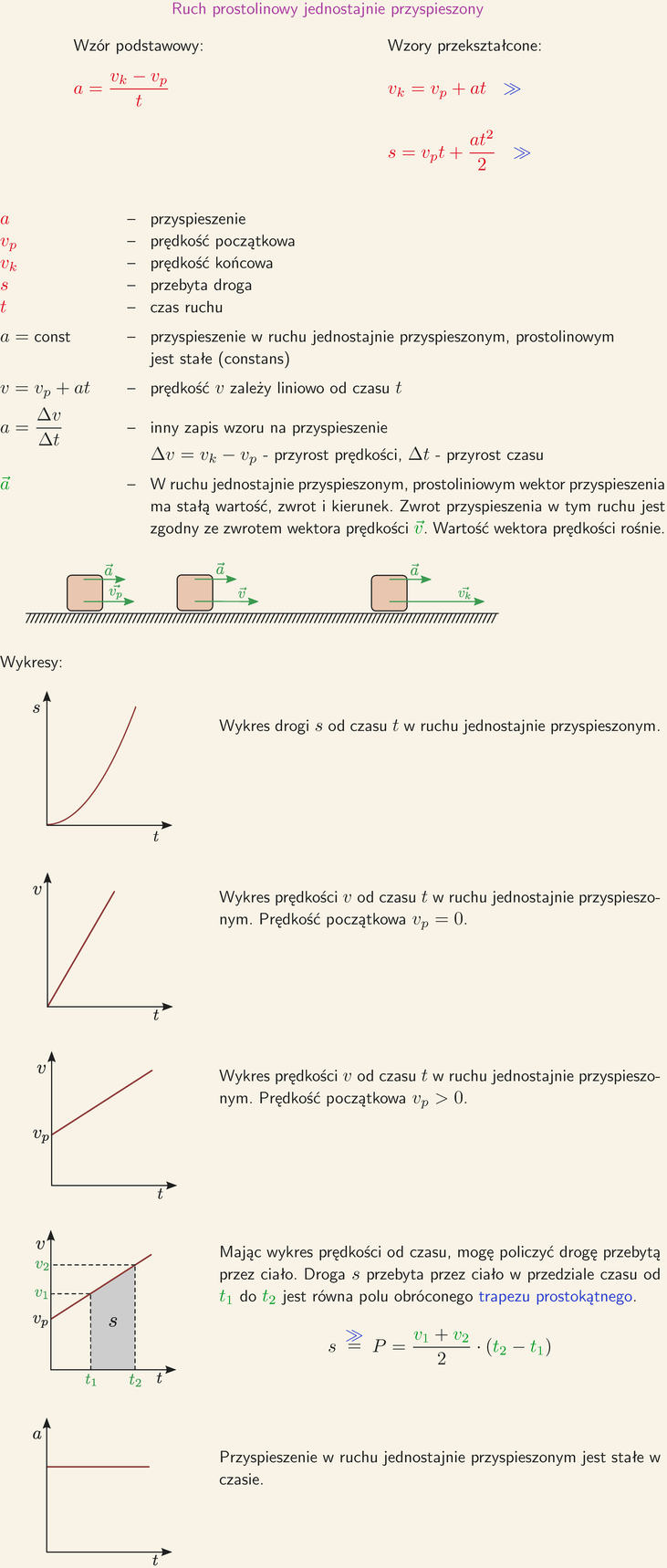
Analiza Wykresów Ruchu Jednostajnie Przyspieszonego i Opóźnionego

Bardzo istotnym elementem zrozumienia ruchu jednostajnie przyspieszonego i opóźnionego jest analiza wykresów. Rozważmy dwa podstawowe typy wykresów: wykres prędkości od czasu (v(t)) oraz wykres drogi od czasu (s(t)).

Wykres v(t): W ruchu jednostajnie przyspieszonym wykres prędkości od czasu jest linią prostą o nachyleniu równym przyspieszeniu. Im większe przyspieszenie, tym bardziej stroma linia. W ruchu jednostajnie opóźnionym również mamy linię prostą, ale o nachyleniu ujemnym, co oznacza, że prędkość maleje w czasie. Pole pod wykresem v(t) reprezentuje przebytą drogę.

Wykres s(t): W ruchu jednostajnie przyspieszonym wykres drogi od czasu jest parabolą. Oznacza to, że droga rośnie w czasie coraz szybciej. W ruchu jednostajnie opóźnionym, zanim ciało się zatrzyma, wykres również będzie fragmentem paraboli, ale z coraz mniejszym przyrostem drogi w czasie. Po zatrzymaniu, droga pozostaje stała.

Zadania z analizą wykresów mogą polegać na odczytywaniu wartości prędkości i przyspieszenia w określonym momencie czasu, obliczaniu drogi na podstawie pola pod wykresem, lub określeniu rodzaju ruchu na podstawie kształtu wykresu.

Zadanie 4: Analiza Wykresu v(t)

Dany jest wykres prędkości od czasu. Przez pierwsze 5 sekund prędkość rośnie liniowo od 0 m/s do 10 m/s. Następnie, przez kolejne 3 sekundy, prędkość pozostaje stała na poziomie 10 m/s. Oblicz przyspieszenie w pierwszych 5 sekundach oraz całkowitą drogę przebytą przez ciało.

Rozwiązanie:

Dane:

• Przedział czasu 1: t1 = 5 s, v0 = 0 m/s, v1 = 10 m/s
• Przedział czasu 2: t2 = 3 s, v2 = 10 m/s (stała prędkość)

Szukane:

• Przyspieszenie (a) w przedziale 1
• Całkowita droga (s)

Obliczamy przyspieszenie w przedziale 1: a = (v1 - v0) / t1 = (10 m/s - 0 m/s) / 5 s = 2 m/s²

Obliczamy drogę w przedziale 1: s1 = v0 * t1 + (1/2) * a * t1² = 0 * 5 s + (1/2) * 2 m/s² * (5 s)² = 25 m

Obliczamy drogę w przedziale 2 (ruch jednostajny): s2 = v2 * t2 = 10 m/s * 3 s = 30 m

Obliczamy całkowitą drogę: s = s1 + s2 = 25 m + 30 m = 55 m

Odpowiedź: Przyspieszenie w pierwszych 5 sekundach wynosi 2 m/s², a całkowita droga przebytą przez ciało to 55 m.

Zadanie 5: Rzut Pionowy w Górę

Ciało zostało rzucone pionowo w górę z prędkością początkową 15 m/s. Oblicz maksymalną wysokość, na jaką wzniesie się ciało oraz czas, po którym spadnie z powrotem na ziemię. (Przyjmij g = 9.81 m/s²)

Rozwiązanie:

Dane:

• Prędkość początkowa (v0) = 15 m/s
• Przyspieszenie (a) = -g = -9.81 m/s² (przyspieszenie ziemskie działa przeciwnie do kierunku ruchu)

Szukane:

• Maksymalna wysokość (h)
• Całkowity czas lotu (t_całkowity)

W najwyższym punkcie prędkość ciała wynosi 0 m/s. Obliczamy czas wznoszenia (t_wznoszenia) do najwyższego punktu: v = v0 + a * t_wznoszenia => 0 = 15 m/s - 9.81 m/s² * t_wznoszenia => t_wznoszenia = 15 m/s / 9.81 m/s² ≈ 1.53 s

Obliczamy maksymalną wysokość (h) korzystając z wzoru: h = v0 * t_wznoszenia + (1/2) * a * t_wznoszenia² h = 15 m/s * 1.53 s + (1/2) * (-9.81 m/s²) * (1.53 s)² ≈ 22.95 m - 11.47 m ≈ 11.48 m

Czas spadania z powrotem na ziemię jest równy czasowi wznoszenia (pomijając opór powietrza). Zatem całkowity czas lotu: t_całkowity = 2 * t_wznoszenia ≈ 2 * 1.53 s ≈ 3.06 s

Odpowiedź: Maksymalna wysokość, na jaką wzniesie się ciało, wynosi około 11.48 m, a całkowity czas lotu to około 3.06 s.

Wskazówki do rozwiązywania zadań

• Zawsze zacznij od wypisania danych i szukanych. Upewnij się, że wszystkie jednostki są zgodne.
• Zastanów się, jakie wzory są odpowiednie do danego zadania. Często pomocny jest rysunek ilustrujący sytuację.
• Przekształcaj wzory algebraicznie, zanim wstawisz wartości liczbowe. Zmniejsza to ryzyko błędów.
• Sprawdzaj jednostki obliczone wartości. Czy wynik ma sens w kontekście zadania?
• Nie bój się korzystać z kalkulatora. Skup się na zrozumieniu fizyki, a kalkulator niech Ci pomoże w obliczeniach.

Pamiętaj, że praktyka czyni mistrza. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz ruch jednostajnie przyspieszony i opóźniony, a rozwiązywanie problemów stanie się dla Ciebie łatwiejsze i przyjemniejsze. Powodzenia!