Rozszerzanie I Skracanie Ułamków Uzupełnij

Ułamki stanowią fundamentalną część matematyki, znajdując zastosowanie w wielu aspektach naszego życia, od gotowania i mierzenia, po finanse i inżynierię. Zrozumienie operacji na ułamkach, takich jak rozszerzanie i skracanie, jest kluczowe do wykonywania obliczeń i rozwiązywania problemów związanych z ułamkami. Niniejszy artykuł szczegółowo omówi te dwie ważne techniki, wyjaśni ich zasady i zaprezentuje praktyczne zastosowania.

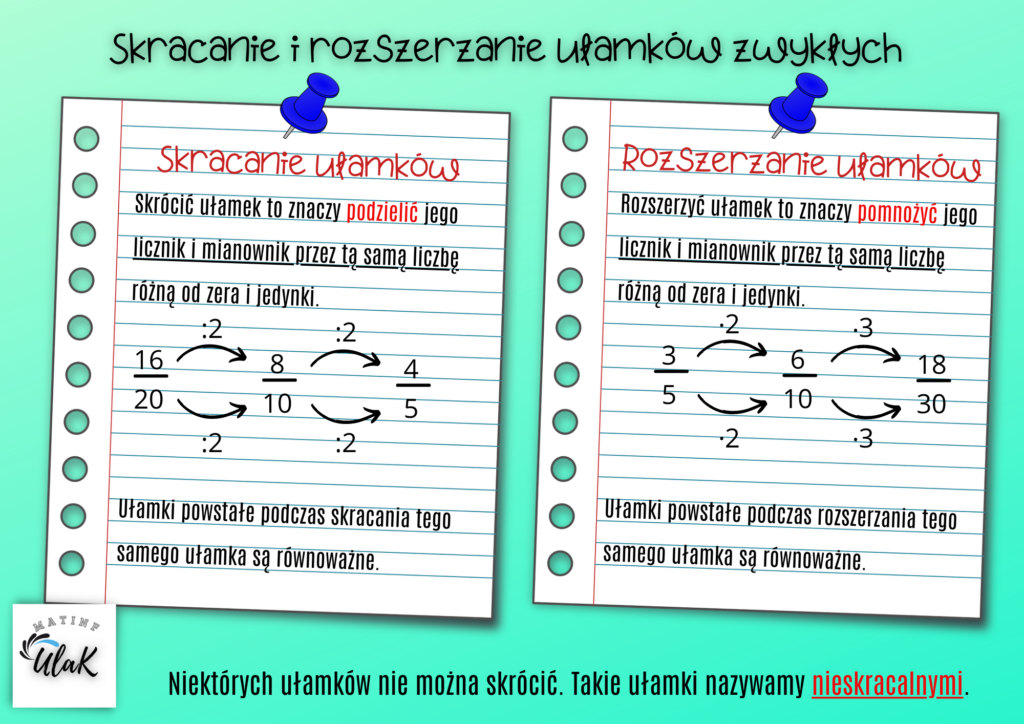
Rozszerzanie Ułamków

Rozszerzanie ułamka polega na pomnożeniu zarówno jego licznika, jak i mianownika przez tę samą liczbę różną od zera. Kluczowe jest zrozumienie, że rozszerzanie ułamka nie zmienia jego wartości, a jedynie jego wygląd. Nowy ułamek, chociaż zapisany innymi liczbami, reprezentuje dokładnie tę samą część całości.

Zasada Rozszerzania

Podstawą rozszerzania ułamka jest prosta zasada: pomnożenie licznika i mianownika przez tę samą liczbę nie zmienia wartości ułamka. Można to zapisać matematycznie jako:

a/b = (a * k) / (b * k), gdzie k ≠ 0

Gdzie:

• a to licznik ułamka.
• b to mianownik ułamka.
• k to liczba, przez którą rozszerzamy ułamek (tzw. współczynnik rozszerzania).

Jak Rozszerzać Ułamki?

Proces rozszerzania jest prosty i składa się z kilku kroków:

1. Wybierz współczynnik rozszerzania (k): Jest to liczba, przez którą pomnożysz zarówno licznik, jak i mianownik. Wybór współczynnika często zależy od konkretnego problemu i celu rozszerzania.
2. Pomnóż licznik przez współczynnik: Otrzymasz nowy licznik rozszerzonego ułamka.
3. Pomnóż mianownik przez współczynnik: Otrzymasz nowy mianownik rozszerzonego ułamka.
4. Zapisz nowy ułamek: Zapisz ułamek z nowym licznikiem i nowym mianownikiem.

Przykład: Rozszerz ułamek 1/3 przez 2.

Krok 1: Współczynnik rozszerzania (k) = 2

Krok 2: Nowy licznik = 1 * 2 = 2

Krok 3: Nowy mianownik = 3 * 2 = 6

Krok 4: Nowy ułamek = 2/6

Zatem, ułamek 1/3 rozszerzony przez 2 to 2/6. Zauważ, że 1/3 i 2/6 reprezentują tę samą wartość.

Dlaczego Rozszerzamy Ułamki?

Rozszerzanie ułamków jest niezwykle przydatne w kilku sytuacjach:

• Porównywanie ułamków: Kiedy chcemy porównać dwa lub więcej ułamków o różnych mianownikach, rozszerzenie ich do wspólnego mianownika ułatwia porównanie ich wielkości.
• Dodawanie i odejmowanie ułamków: Dodawanie i odejmowanie ułamków jest możliwe tylko wtedy, gdy mają one wspólny mianownik. Rozszerzanie pozwala na doprowadzenie ułamków do wspólnego mianownika, co umożliwia wykonanie operacji.
• Upraszczanie obliczeń: W niektórych przypadkach rozszerzenie ułamka może ułatwić dalsze obliczenia, np. w proporcjach lub zadaniach tekstowych.

Skracanie Ułamków

Skracanie ułamka to operacja odwrotna do rozszerzania. Polega na podzieleniu zarówno licznika, jak i mianownika ułamka przez ich wspólny dzielnik (liczbę, która dzieli oba bez reszty). Podobnie jak w przypadku rozszerzania, skracanie ułamka nie zmienia jego wartości, a jedynie jego wygląd. Otrzymujemy ułamek o mniejszych liczbach, ale reprezentujący tę samą część całości.

Zasada Skracania

Zasada skracania jest analogiczna do zasady rozszerzania: podzielenie licznika i mianownika przez tę samą liczbę (ich wspólny dzielnik) nie zmienia wartości ułamka. Matematycznie:

a/b = (a / k) / (b / k), gdzie k jest wspólnym dzielnikiem a i b.

Gdzie:

• a to licznik ułamka.
• b to mianownik ułamka.
• k to wspólny dzielnik licznika i mianownika.

Jak Skracać Ułamki?

Proces skracania wygląda następująco:

1. Znajdź wspólny dzielnik licznika i mianownika: Poszukaj liczby, przez którą dzielą się zarówno licznik, jak i mianownik bez reszty. Najlepiej jest znaleźć największy wspólny dzielnik (NWD), aby skrócić ułamek do najprostszej postaci.
2. Podziel licznik przez wspólny dzielnik: Otrzymasz nowy licznik skróconego ułamka.
3. Podziel mianownik przez wspólny dzielnik: Otrzymasz nowy mianownik skróconego ułamka.
4. Zapisz nowy ułamek: Zapisz ułamek z nowym licznikiem i nowym mianownikiem.

Przykład: Skróć ułamek 6/8.

Krok 1: Wspólny dzielnik licznika i mianownika = 2 (NWD(6,8) = 2)

Krok 2: Nowy licznik = 6 / 2 = 3

Krok 3: Nowy mianownik = 8 / 2 = 4

Krok 4: Nowy ułamek = 3/4

Zatem, ułamek 6/8 skrócony to 3/4. Oba ułamki reprezentują tę samą wartość.

Dlaczego Skracamy Ułamki?

Skracanie ułamków jest przydatne, ponieważ:

• Upraszcza ułamki: Skrócony ułamek ma mniejsze liczby, co ułatwia dalsze obliczenia i interpretację.
• Ułatwia porównywanie ułamków: Czasami skracanie ułamków pozwala na szybsze porównanie ich wielkości, szczególnie gdy mianowniki po skróceniu stają się mniejsze i łatwiejsze do porównania.
• Przedstawia ułamek w najprostszej postaci: Ułamek, którego licznik i mianownik nie mają już wspólnych dzielników (oprócz 1), jest w najprostszej postaci, co jest preferowane w matematyce.

Real-world examples

Rozważmy przepis na ciasto, który wymaga 1/2 szklanki mąki. Jeśli chcemy zrobić podwójną porcję, musimy rozszerzyć ułamek 1/2 przez 2, uzyskując 2/4. Chociaż 1/2 i 2/4 reprezentują tę samą ilość, użycie 2/4 może być mniej intuicyjne w tym kontekście. Jednak jeśli przepis wymaga 3/4 szklanki cukru, a mamy tylko miarkę 1/4 szklanki, możemy rozszerzyć 3/4 do 6/8, co oznacza, że potrzebujemy 6 miarek po 1/8 szklanki (co odpowiada miarce 1/4).

W finansach, jeśli inwestycja wzrosła o 25/100, możemy skrócić ten ułamek do 1/4, co daje nam bardziej zrozumiałą informację o wzroście o jedną czwartą. Podobnie, jeśli raport wskazuje, że 75/100 pracowników jest zadowolonych, skracając do 3/4, łatwo stwierdzamy, że trzy czwarte załogi jest usatysfakcjonowane.

W budownictwie, jeśli plan zakłada użycie 12/16 cala grubości płyty, skracając ten ułamek do 3/4, uzyskujemy standardowy wymiar łatwiejszy do znalezienia i obróbki.

Podsumowanie

Rozszerzanie i skracanie ułamków to podstawowe operacje, które pozwalają na manipulowanie ułamkami bez zmiany ich wartości. Rozszerzanie jest przydatne do porównywania, dodawania i odejmowania ułamków, podczas gdy skracanie upraszcza ułamki i przedstawia je w najprostszej postaci. Zrozumienie tych operacji jest kluczowe do rozwiązywania problemów matematycznych i stosowania ułamków w praktyce.

Zachęcamy do dalszego ćwiczenia rozszerzania i skracania ułamków. Wykorzystaj przykłady z życia codziennego, aby utrwalić zdobytą wiedzę. Im więcej będziesz ćwiczyć, tym łatwiej i pewniej będziesz posługiwać się ułamkami!