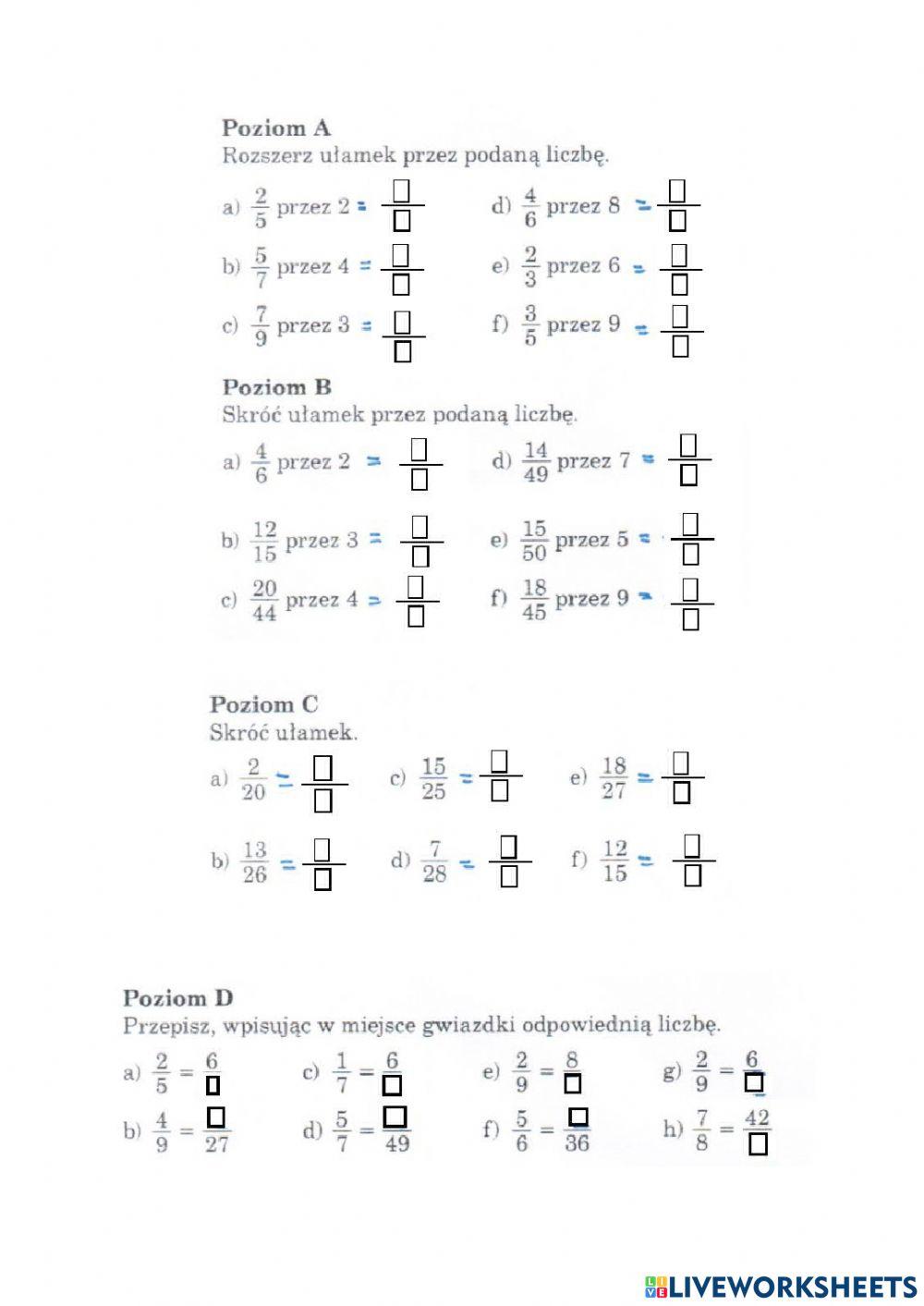
Rozszerzanie I Skracanie Ułamków Klasa 4 Karta Pracy

Rozszerzanie i skracanie ułamków to fundament matematyki w klasie 4. Dzieci uczą się, jak manipulować ułamkami, zachowując ich wartość. Opanowanie tych umiejętności otwiera drzwi do bardziej zaawansowanych koncepcji, takich jak dodawanie, odejmowanie, mnożenie i dzielenie ułamków. Przyjrzyjmy się bliżej temu zagadnieniu.

Rozszerzanie ułamków to proces mnożenia zarówno licznika, jak i mianownika przez tę samą liczbę. Na przykład, ułamek 1/2 możemy rozszerzyć przez 2, otrzymując 2/4. Możemy go również rozszerzyć przez 3, otrzymując 3/6. Wszystkie te ułamki – 1/2, 2/4 i 3/6 – reprezentują tę samą wartość.

Praktyczne ćwiczenia pomagają zrozumieć tę koncepcję. Rozważmy ułamek 2/5. Możemy go rozszerzyć przez 4. Mnożymy licznik (2) przez 4, co daje nam 8. Następnie mnożymy mianownik (5) przez 4, co daje nam 20. W ten sposób otrzymujemy ułamek 8/20. Ułamek 8/20 jest równoważny ułamkowi 2/5.

Kolejny przykład: rozszerz ułamek 3/7 przez 6. Mnożymy licznik (3) przez 6, co daje nam 18. Następnie mnożymy mianownik (7) przez 6, co daje nam 42. Otrzymujemy ułamek 18/42. Ułamek 18/42 jest równoważny ułamkowi 3/7.

Inny przykład, tym razem z większymi liczbami: rozszerz ułamek 5/12 przez 10. Mnożymy licznik (5) przez 10, co daje nam 50. Następnie mnożymy mianownik (12) przez 10, co daje nam 120. Otrzymujemy ułamek 50/120. Ułamek 50/120 jest równoważny ułamkowi 5/12.

Teraz przejdźmy do skracania ułamków. Skracanie ułamków to proces dzielenia zarówno licznika, jak i mianownika przez tę samą liczbę. Celem jest uzyskanie ułamka w najprostszej postaci, czyli takiego, którego licznik i mianownik nie mają już wspólnych dzielników (poza 1).

Aby skrócić ułamek, musimy znaleźć wspólny dzielnik licznika i mianownika. Na przykład, rozważmy ułamek 4/8. Zarówno licznik (4), jak i mianownik (8) są podzielne przez 4. Dzielimy licznik (4) przez 4, co daje nam 1. Następnie dzielimy mianownik (8) przez 4, co daje nam 2. W ten sposób otrzymujemy ułamek 1/2. Ułamek 1/2 jest najprostszą postacią ułamka 4/8.

Kolejny przykład: skróć ułamek 6/9. Zarówno licznik (6), jak i mianownik (9) są podzielne przez 3. Dzielimy licznik (6) przez 3, co daje nam 2. Następnie dzielimy mianownik (9) przez 3, co daje nam 3. Otrzymujemy ułamek 2/3. Ułamek 2/3 jest najprostszą postacią ułamka 6/9.

Inny przykład: skróć ułamek 10/15. Zarówno licznik (10), jak i mianownik (15) są podzielne przez 5. Dzielimy licznik (10) przez 5, co daje nam 2. Następnie dzielimy mianownik (15) przez 5, co daje nam 3. Otrzymujemy ułamek 2/3. Ułamek 2/3 jest najprostszą postacią ułamka 10/15.

Przy skracaniu ułamków ważne jest, aby znaleźć największy wspólny dzielnik (NWD) licznika i mianownika. Dzielenie przez NWD od razu prowadzi do najprostszej postaci ułamka. Na przykład, rozważmy ułamek 12/18. Największym wspólnym dzielnikiem liczb 12 i 18 jest 6. Dzielimy licznik (12) przez 6, co daje nam 2. Następnie dzielimy mianownik (18) przez 6, co daje nam 3. Otrzymujemy ułamek 2/3.

Zadania na rozszerzanie ułamków

Rozszerz ułamek 1/3 przez 5.
Rozszerz ułamek 2/7 przez 3.
Rozszerz ułamek 4/9 przez 2.
Rozszerz ułamek 3/5 przez 4.
Rozszerz ułamek 5/8 przez 6.
Rozszerz ułamek 1/6 przez 7.
Rozszerz ułamek 2/11 przez 2.
Rozszerz ułamek 3/10 przez 5.
Rozszerz ułamek 4/13 przez 3.
Rozszerz ułamek 5/14 przez 4.
Rozszerz ułamek 1/4 przez 8.
Rozszerz ułamek 2/9 przez 6.
Rozszerz ułamek 3/8 przez 7.
Rozszerz ułamek 4/11 przez 5.
Rozszerz ułamek 5/16 przez 2.

Zadania na skracanie ułamków

Skróć ułamek 8/12.
Skróć ułamek 10/16.
Skróć ułamek 12/18.
Skróć ułamek 14/21.
Skróć ułamek 15/25.
Skróć ułamek 9/15.
Skróć ułamek 16/20.
Skróć ułamek 18/24.
Skróć ułamek 20/30.
Skróć ułamek 22/33.
Skróć ułamek 6/10.
Skróć ułamek 14/16.
Skróć ułamek 8/20.
Skróć ułamek 10/12.
Skróć ułamek 12/16.

Wykonując te zadania, dzieci ćwiczą umiejętność rozszerzania i skracania ułamków, co umacnia ich zrozumienie tych koncepcji. Regularne ćwiczenia są kluczem do opanowania matematyki.

Dodatkowo, można wykorzystać wizualne pomoce, takie jak koła podzielone na części, aby pokazać równoważność ułamków. Na przykład, koło podzielone na dwie równe części (1/2) można przedstawić jako koło podzielone na cztery równe części (2/4), pokazując, że obie reprezentacje oznaczają tę samą część całości.

Podczas nauki rozszerzania i skracania ułamków ważne jest, aby podkreślić, że działania te nie zmieniają wartości ułamka, a jedynie zmieniają jego reprezentację. Jest to kluczowe zrozumienie, które pomaga uczniom uniknąć błędów w przyszłości.

Warto również wprowadzić gry i zabawy edukacyjne, które sprawią, że nauka stanie się bardziej angażująca i przyjemna. Można wykorzystać karty z ułamkami, które dzieci będą musiały rozszerzyć lub skrócić, lub stworzyć grę planszową, w której postęp zależy od prawidłowego rozwiązywania zadań z ułamkami.

Pamiętajmy, że cierpliwość i pozytywne nastawienie są bardzo ważne podczas nauki. Każde dziecko uczy się w swoim własnym tempie, dlatego ważne jest, aby dostosować tempo nauki do indywidualnych potrzeb ucznia. Zachęcajmy dzieci do zadawania pytań i wyjaśniajmy wątpliwości. W ten sposób możemy pomóc im zbudować solidne fundamenty matematyczne, które przydadzą im się w dalszej edukacji.