Rozkład Materiału Matematyka Klasa 1 Liceum Nowa Era

Dzień dobry wszystkim! Często pytacie mnie o rozkład materiału z matematyki dla klasy 1 liceum, szczególnie z podręcznika Nowej Ery. Spróbuję Wam to przybliżyć w prosty i zrozumiały sposób, żebyście wiedzieli, czego się spodziewać w ciągu roku. Pamiętajcie, że to tylko orientacyjny plan, a nauczyciele mogą go modyfikować w zależności od potrzeb klasy.

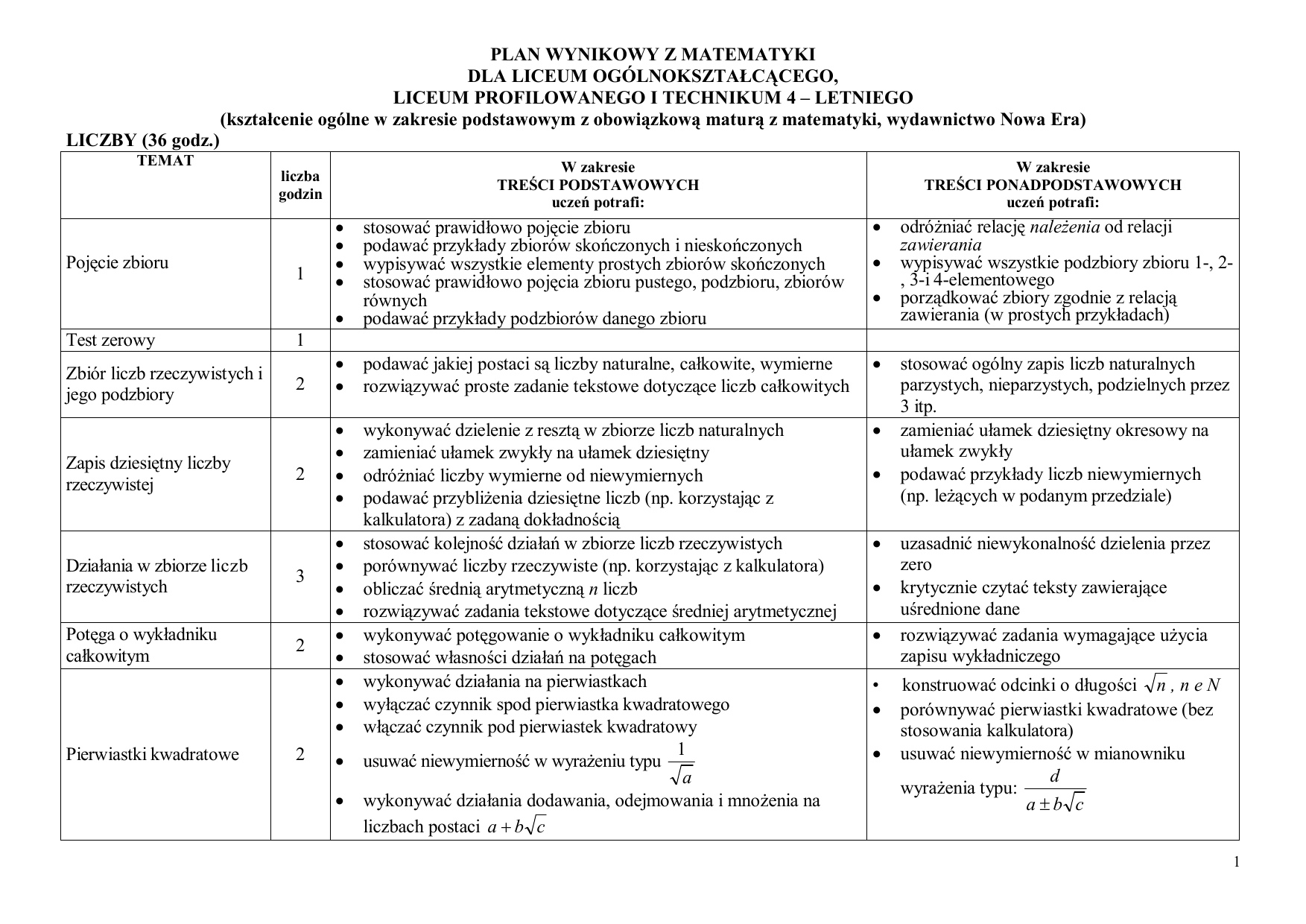
Zazwyczaj rok szkolny zaczynamy od powtórki wiadomości ze szkoły podstawowej. To bardzo ważne, żeby solidnie przypomnieć sobie podstawy, bo wszystko, czego się nauczycie w liceum, bazuje na tej wiedzy. Skupiamy się na takich zagadnieniach jak: działania na liczbach (dodawanie, odejmowanie, mnożenie, dzielenie), ułamki zwykłe i dziesiętne, procenty, kolejność wykonywania działań, potęgi i pierwiastki. Sprawdzamy, czy dobrze operujecie wzorami skróconego mnożenia i czy potraficie rozwiązywać proste równania i nierówności. Jeżeli macie z czymś problem, to jest to idealny moment, żeby poprosić o pomoc i wszystko sobie wyjaśnić.

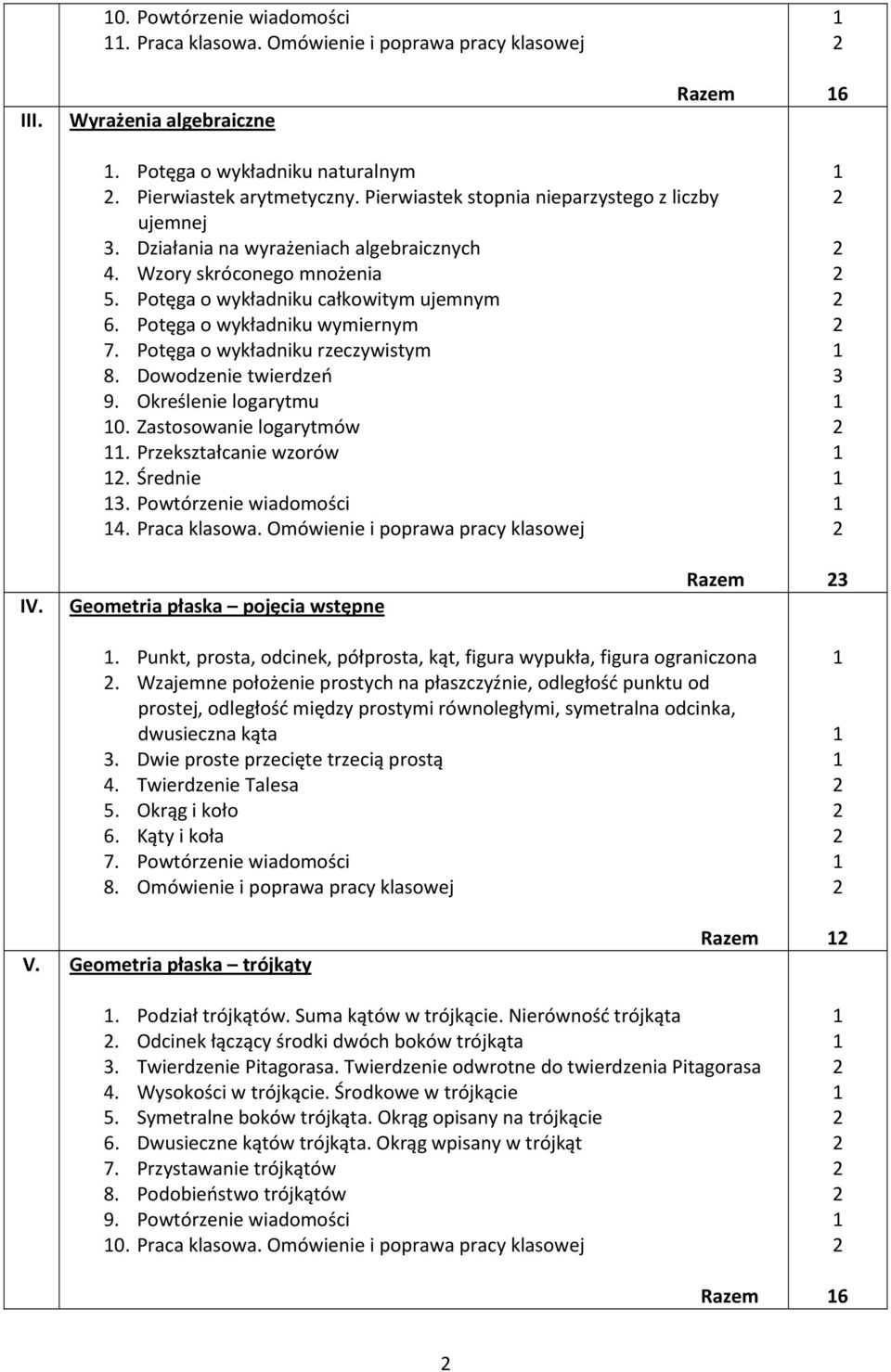
Następnie przechodzimy do pierwszego, dużego działu, czyli liczby rzeczywiste. Dowiecie się czym są liczby naturalne, całkowite, wymierne i niewymierne. Będziecie uczyć się o przedziałach liczbowych – jak je zapisywać, rysować na osi liczbowej i wykonywać na nich działania (np. sumę, iloczyn, różnicę). Dużo ćwiczeń będzie poświęconych obliczeniom procentowym, w tym obliczaniu procentu danej liczby, obliczaniu jakim procentem jednej liczby jest druga liczba oraz obliczaniu liczby, gdy dany jest jej procent. Nauczymy się również obliczać błędy przybliżeń – bezwzględny i względny. Będziemy też pracować z wyrażeniami algebraicznymi – upraszczać je, redukować wyrazy podobne, wyłączać wspólny czynnik przed nawias. To wszystko jest bardzo przydatne w dalszej nauce matematyki i w życiu codziennym.

Kolejny ważny dział to zbiory. Poznacie podstawowe pojęcia związane ze zbiorami: co to jest zbiór, jakie są rodzaje zbiorów (np. zbiór pusty, zbiór skończony, zbiór nieskończony), jak zapisywać zbiory (np. przez wyliczenie elementów, przez podanie cechy). Nauczycie się wykonywać działania na zbiorach, takie jak suma zbiorów, iloczyn zbiorów (część wspólna), różnica zbiorów i dopełnienie zbioru. Będziecie również rysować diagramy Venna, żeby wizualizować zbiory i zależności między nimi.

Funkcje – podstawa matematyki w liceum

Po zbiorach zaczynamy przygodę z funkcjami. To jeden z najważniejszych działów w całej matematyce licealnej. Najpierw dowiecie się, co to jest funkcja, czym jest argument funkcji, wartość funkcji, dziedzina funkcji i zbiór wartości funkcji. Będziecie uczyć się o różnych sposobach przedstawiania funkcji: za pomocą wzoru, tabeli, grafu (strzałek) i wykresu. Bardzo dużo czasu poświęcimy na rysowanie wykresów funkcji i odczytywanie z nich różnych informacji: miejsca zerowe, przedziały, w których funkcja rośnie, maleje lub jest stała, wartość największą i najmniejszą funkcji w danym przedziale, punkty przecięcia z osiami układu współrzędnych.

Szczególną uwagę zwrócimy na funkcję liniową. Dowiecie się, jak wygląda wzór funkcji liniowej (y = ax + b), co oznaczają współczynniki a i b, jak rysować wykres funkcji liniowej i jak znaleźć równanie prostej przechodzącej przez dwa punkty. Nauczycie się również rozwiązywać zadania związane z interpretacją współczynników funkcji liniowej (np. współczynnik kierunkowy mówi o tym, czy funkcja rośnie, maleje czy jest stała). Będziecie także analizować wzajemne położenie dwóch prostych (czy są równoległe, prostopadłe, przecinające się).

Następnie omówimy funkcję kwadratową. Poznacie wzór ogólny funkcji kwadratowej (y = ax^2 + bx + c), postać kanoniczną i postać iloczynową. Nauczycie się obliczać miejsca zerowe funkcji kwadratowej (jeśli istnieją) za pomocą delty (Δ) i wzorów na x1 i x2. Będziecie rysować wykres funkcji kwadratowej (parabolę) i odczytywać z niego różne informacje: wierzchołek paraboli, oś symetrii paraboli, przedziały, w których funkcja rośnie lub maleje, wartość największą i najmniejszą funkcji w danym przedziale. Będziecie również rozwiązywać zadania optymalizacyjne z wykorzystaniem funkcji kwadratowej (np. znajdowanie największej wartości pola prostokąta o danym obwodzie).

Kolejnym tematem są własności funkcji. Będziemy rozmawiać o takich pojęciach jak: monotoniczność funkcji (funkcja rosnąca, malejąca, stała), parzystość i nieparzystość funkcji, okresowość funkcji, miejsca zerowe funkcji, zbiór wartości funkcji, wartość największa i najmniejsza funkcji w danym przedziale. Będziecie uczyć się, jak rozpoznawać te własności na podstawie wykresu funkcji i jak je udowadniać algebraicznie.

W dalszej części roku zajmiemy się geometrią. Zaczniemy od podstawowych pojęć geometrii płaskiej: punkty, proste, odcinki, kąty (rodzaje kątów, miara kątów), trójkąty (rodzaje trójkątów, cechy przystawania trójkątów, cechy podobieństwa trójkątów), czworokąty (równoległoboki, romby, prostokąty, kwadraty, trapezy), koła i okręgi. Będziecie uczyć się obliczać pola i obwody różnych figur geometrycznych, korzystać z twierdzenia Pitagorasa i twierdzenia Talesa.

Następnie przejdziemy do trygonometrii kąta ostrego. Poznacie definicje funkcji trygonometrycznych kąta ostrego (sinus, cosinus, tangens, cotangens) w trójkącie prostokątnym. Będziecie uczyć się obliczać wartości funkcji trygonometrycznych dla kątów ostrych, korzystać z tablic trygonometrycznych lub kalkulatora. Nauczycie się rozwiązywać zadania praktyczne z wykorzystaniem trygonometrii (np. obliczanie wysokości budynku na podstawie kąta widzenia).

Pod koniec roku szkolnego omówimy statystykę opisową. Dowiecie się, jak gromadzić i porządkować dane statystyczne, jak przedstawiać je w postaci tabel, wykresów (np. histogramów, diagramów kołowych). Będziecie uczyć się obliczać miary statystyczne: średnią arytmetyczną, medianę, dominantę (modę), odchylenie standardowe. Nauczycie się interpretować te miary i wyciągać wnioski na podstawie danych statystycznych.

Pamiętajcie, że ten rozkład materiału jest tylko orientacyjny. Nauczyciel może go dostosować do potrzeb i możliwości klasy. Ważne jest, żeby regularnie się uczyć, zadawać pytania, jeśli coś jest niezrozumiałe, i nie bać się prosić o pomoc. Powodzenia!