Równoległoboki I Romby Kl 5 Sprawdzian

Drodzy nauczyciele klas piątych, przygotowanie uczniów do sprawdzianu z równoległoboków i rombów wymaga solidnego zrozumienia podstawowych koncepcji geometrycznych. Ten artykuł ma na celu dostarczenie Wam praktycznych wskazówek, które pomogą w efektywnym nauczaniu tego tematu, identyfikacji powszechnych błędów uczniów oraz uatrakcyjnieniu lekcji.

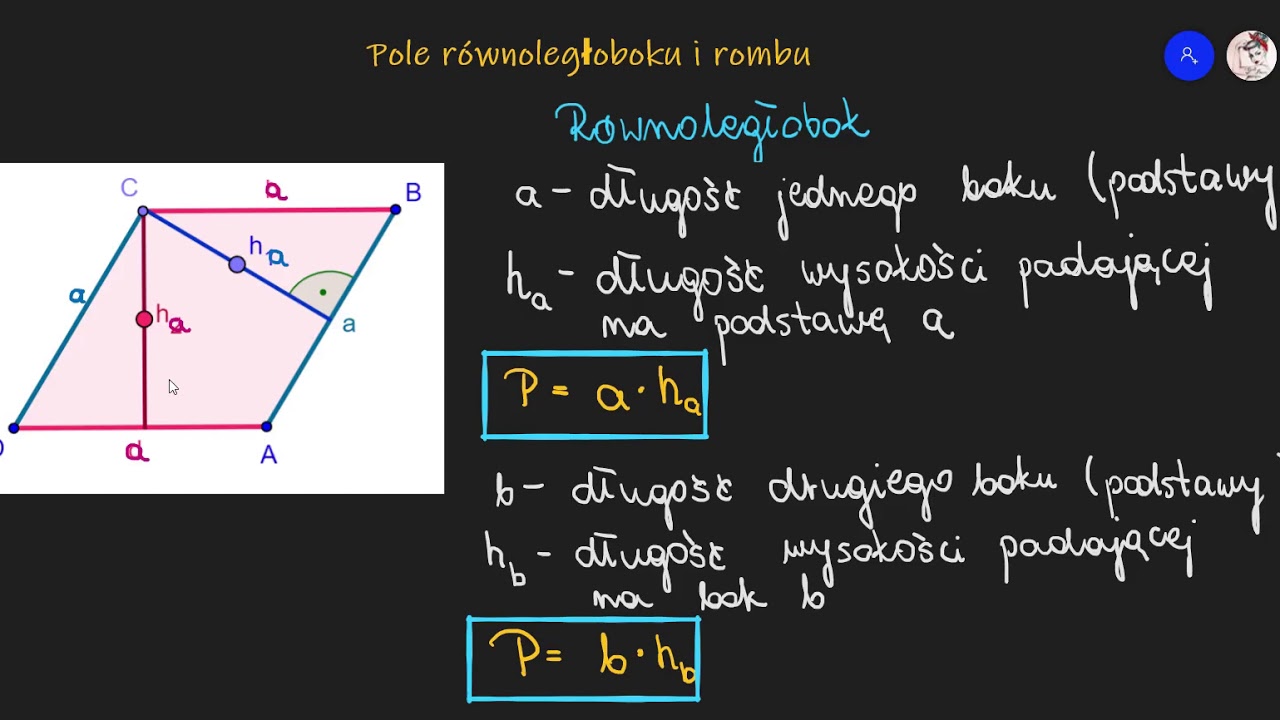
Podstawowe pojęcia: Równoległoboki

Zacznijmy od równoległoboku. Kluczowe jest, aby uczniowie zrozumieli definicję: równoległobok to czworokąt, który ma dwie pary boków równoległych. Podkreślcie, że równoległość boków jest fundamentalną cechą równoległoboku. Pomocne może być użycie wizualnych pomocy, takich jak modele równoległoboków wykonane z papieru lub patyczków. Demonstracja, jak można przekształcić prostokąt w równoległobok poprzez "przechylenie" go, zachowując równoległość boków, bardzo dobrze działa na wyobraźnię.

Jak efektywnie tłumaczyć właściwości równoległoboków:

• Przeciwległe boki są równe. Użyjcie linijki, aby uczniowie sami zmierzyli przeciwległe boki różnych równoległoboków i potwierdzili tę zależność.
• Przeciwległe kąty są równe. W tym przypadku przyda się kątomierz. Zachęćcie uczniów do pomiaru kątów w równoległobokach i porównania ich.
• Suma miar kątów wewnętrznych wynosi 360°. To jest ogólna zasada dla każdego czworokąta, ale warto ją przypomnieć i potwierdzić również dla równoległoboków.
• Przekątne przecinają się w połowie. Narysujcie przekątne w równoległoboku i zmierzcie odcinki, na które dzielą się te przekątne w punkcie przecięcia.

Romb: Szczególny przypadek równoległoboku

Teraz przejdźmy do rombu. Wyjaśnijcie, że romb jest szczególnym typem równoległoboku, który ma wszystkie boki równe. Zaznaczcie, że skoro romb jest równoległobokiem, to posiada wszystkie właściwości równoległoboku, a dodatkowo ma swoje unikalne cechy.

Dodatkowe właściwości rombu:

• Wszystkie boki są równe. To definicja rombu, ale warto ją podkreślić.
• Przekątne przecinają się pod kątem prostym. Użyjcie kątomierza, aby to zademonstrować.
• Przekątne są dwusiecznymi kątów wewnętrznych rombu. Oznacza to, że każda przekątna dzieli kąt w wierzchołku na dwie równe części.

Powszechne błędy i jak im zapobiegać

Uczniowie często popełniają pewne typowe błędy. Ważne jest, aby być ich świadomym i aktywnie im zapobiegać:

• Mylenie równoległoboku z trapezem. Wyraźnie pokażcie różnicę: równoległobok ma dwie pary boków równoległych, a trapez ma tylko jedną parę.
• Nierozumienie, że romb jest równoległobokiem. Podkreślajcie to wielokrotnie! Używajcie diagramów Venna, aby wizualnie pokazać, że zbiór rombów jest podzbiorem zbioru równoległoboków.
• Błędne stosowanie właściwości. Upewnijcie się, że uczniowie rozumieją, kiedy dana właściwość może być użyta. Na przykład, właściwość o przekątnych przecinających się pod kątem prostym dotyczy tylko rombu, a nie każdego równoległoboku.
• Problemy z rysowaniem. Ćwiczcie rysowanie równoległoboków i rombów. Użyjcie kratki w zeszycie, aby ułatwić rysowanie równoległych linii.

Jak uatrakcyjnić lekcję?

Aby nauka była bardziej angażująca, warto wykorzystać różne metody:

• Gry i zabawy. Można zorganizować quiz, w którym uczniowie muszą rozpoznawać równoległoboki i romby na podstawie ich właściwości. Inną opcją jest gra w "zgadnij, jaki to czworokąt", gdzie opisuje się czworokąt, a uczniowie muszą go odgadnąć.
• Zadania praktyczne. Poproście uczniów o znalezienie przykładów równoległoboków i rombów w otoczeniu (np. w architekturze, w wzorach na tkaninach). Mogą zrobić zdjęcia i opisać, jakie właściwości zauważyli.
• Wykorzystanie technologii. Użyjcie programów do geometrii dynamicznej (np. GeoGebra) do interaktywnego demonstrowania właściwości równoległoboków i rombów.
• Praca w grupach. Podzielcie uczniów na grupy i poproście o stworzenie plakatu, na którym przedstawią najważniejsze informacje o równoległobokach i rombach.
• Zagadki i łamigłówki. Wprowadźcie zadania logiczne związane z właściwościami tych figur. Na przykład: "Mam cztery boki, przeciwległe boki są równoległe, a moje przekątne przecinają się pod kątem prostym. Kim jestem?".

Przykładowe zadania na sprawdzian

Oto kilka przykładowych zadań, które mogą pojawić się na sprawdzianie:

1. Narysuj równoległobok i romb. Zaznacz boki równoległe i kąty równe.
2. W równoległoboku jeden z kątów ma miarę 70°. Oblicz miary pozostałych kątów.
3. Obwód rombu wynosi 20 cm. Oblicz długość jednego boku.
4. Czy każdy prostokąt jest równoległobokiem? Uzasadnij odpowiedź.
5. Podaj 3 różnice między rombem a równoległobokiem, który nie jest rombem.

Przygotowanie uczniów do sprawdzianu z równoległoboków i rombów wymaga cierpliwości, jasnego tłumaczenia i różnorodnych metod nauczania. Pamiętajcie, że kluczem do sukcesu jest zrozumienie podstawowych definicji i właściwości. Powodzenia!