Rownania Nierownosci Uklady Rownan Sprawdzian

Stoisz przed sprawdzianem z równań, nierówności i układów równań i czujesz, że ogarnia Cię chaos? Wdech i wydech. Pamiętaj, każdy kiedyś przez to przechodził. Matematyka, choć czasem wydaje się abstrakcyjna, kryje w sobie logiczny porządek, który da się zrozumieć. Ten artykuł ma być Twoim przewodnikiem – pomoże Ci uporządkować wiedzę i poczuć się pewniej przed tym ważnym sprawdzianem.

Równania – fundament algebry

Równanie to, najprościej mówiąc, stwierdzenie, że dwie rzeczy są sobie równe. To jak waga – obie strony muszą być w równowadze. Centralnym celem w rozwiązywaniu równań jest znalezienie wartości niewiadomej (zwykle oznaczanej jako x), dla której ta równość zachodzi. Kluczem jest wykonywanie tych samych operacji po obu stronach równania, aby nie zaburzyć tej równowagi.

Podstawowe typy równań:

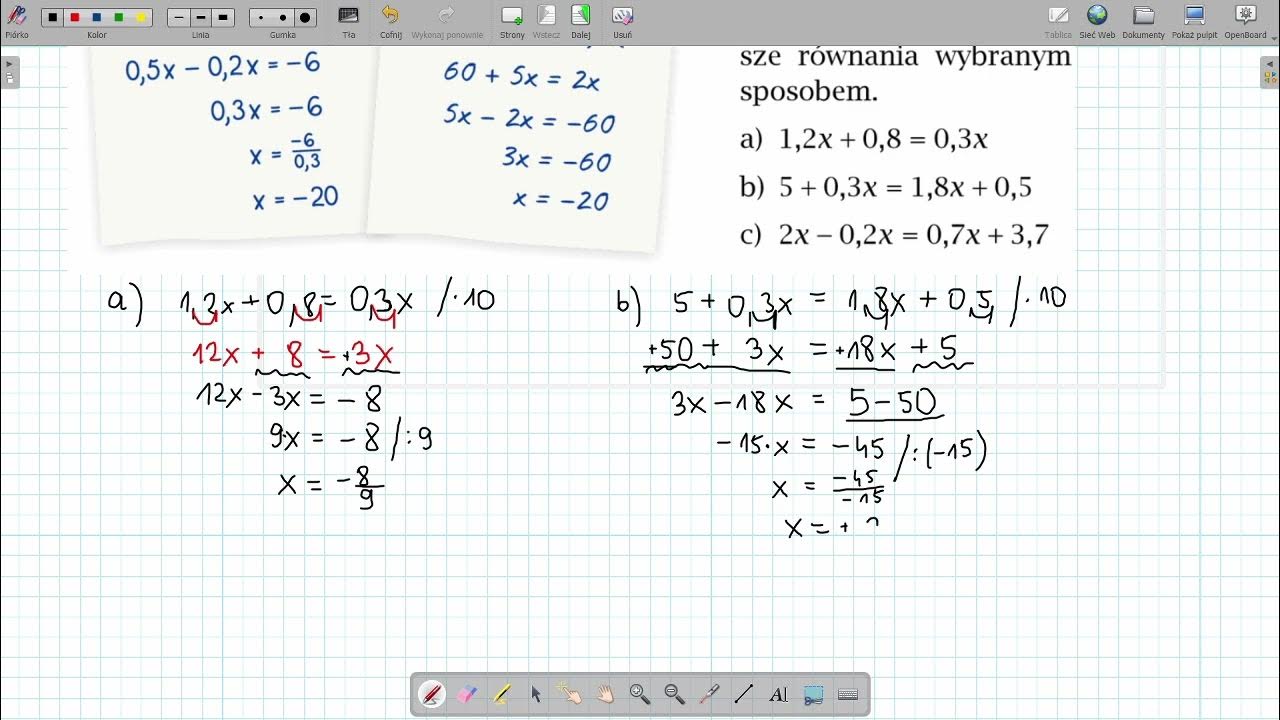
* Równania liniowe: Najprostszy typ, w którym niewiadoma występuje w pierwszej potędze (np. 2x + 3 = 7). Rozwiązuje się je przez przenoszenie wyrazów z niewiadomą na jedną stronę, a liczb na drugą, a następnie podzielenie obu stron przez współczynnik przy x.

* Równania kwadratowe: Zawierają niewiadomą w drugiej potędze (np. x² + 2x + 1 = 0). Tutaj często stosuje się wzór na deltę (Δ) i pierwiastki równania kwadratowego. Pamiętaj, że równanie kwadratowe może mieć dwa rozwiązania, jedno rozwiązanie (gdy Δ = 0), lub brak rozwiązań rzeczywistych (gdy Δ < 0).

* Równania z wartością bezwzględną: Wartość bezwzględna liczby to jej odległość od zera, zawsze nieujemna. Rozwiązując równania z wartością bezwzględną, musisz rozważyć dwa przypadki: gdy wyrażenie wewnątrz wartości bezwzględnej jest dodatnie lub równe zero oraz gdy jest ujemne.

Przykład praktyczny: Wyobraź sobie, że masz równanie 3x + 5 = 14. Odejmujesz 5 od obu stron: 3x = 9. Następnie dzielisz obie strony przez 3: x = 3. Voila! Znalazłeś rozwiązanie.

Nierówności – granice i przedziały

Nierówność, w przeciwieństwie do równania, określa, że jedna wartość jest większa, mniejsza, większa lub równa, albo mniejsza lub równa innej. Zamiast pojedynczej wartości, rozwiązaniem nierówności jest zwykle przedział liczb.

Kluczowe różnice między równaniami a nierównościami:

* Zmiana znaku przy mnożeniu/dzieleniu przez liczbę ujemną: Jeśli mnożysz lub dzielisz obie strony nierówności przez liczbę ujemną, musisz odwrócić znak nierówności. To bardzo ważny detal, który łatwo przeoczyć!

* Przedziały: Rozwiązania nierówności przedstawia się za pomocą przedziałów liczbowych (np. x > 2 oznacza przedział (2, +∞)). Pamiętaj o używaniu nawiasów okrągłych ( ) dla przedziałów otwartych (bez krańców) i nawiasów kwadratowych [ ] dla przedziałów domkniętych (z krańcami).

Przykład: Rozwiąż nierówność 2x – 4 < 6. Dodaj 4 do obu stron: 2x < 10. Podziel obie strony przez 2: x < 5. Rozwiązaniem jest przedział (-∞, 5).

Układy równań – kilka niewiadomych, jedno rozwiązanie

Układ równań to zestaw dwóch lub więcej równań, w których szukamy wspólnych rozwiązań dla wszystkich równań w układzie. Oznacza to, że musisz znaleźć wartości dla wszystkich niewiadomych, które spełniają każde z równań.

Popularne metody rozwiązywania układów równań:

* Metoda podstawiania: Wyznaczasz jedną niewiadomą z jednego równania i podstawiasz ją do drugiego równania.

* Metoda przeciwnych współczynników: Mnożysz jedno lub oba równania przez takie liczby, aby współczynniki przy jednej z niewiadomych były liczbami przeciwnymi. Następnie dodajesz równania stronami, aby wyeliminować tę niewiadomą.

Przykład: Rozważmy układ: x + y = 5 i x – y = 1. Dodając równania stronami, otrzymujemy 2x = 6, więc x = 3. Podstawiając x = 3 do pierwszego równania, otrzymujemy 3 + y = 5, więc y = 2. Rozwiązaniem jest para liczb (x, y) = (3, 2).

Sprawdzian – przygotowanie to klucz

Skoro masz już solidne podstawy teoretyczne, czas na praktyczne przygotowanie do sprawdzianu. Oto kilka wskazówek:

* Rozwiąż zadania z podręcznika i zbioru zadań: To podstawa. Im więcej zadań rozwiążesz, tym lepiej zrozumiesz materiał i szybciej będziesz rozwiązywał problemy.

* Powtórz definicje i wzory: Upewnij się, że rozumiesz definicje równań, nierówności i układów równań, oraz że znasz wszystkie niezbędne wzory (np. wzór na deltę).

* Rozwiąż stare sprawdziany i kartkówki: To doskonały sposób na sprawdzenie swojej wiedzy i zobaczenie, jakiego typu zadania pojawiają się na sprawdzianach.

* Ucz się z kolegami i koleżankami: Wspólna nauka może być bardzo efektywna. Możecie się nawzajem pytać, tłumaczyć trudne zagadnienia i rozwiązywać zadania wspólnie.

* Nie zostawiaj wszystkiego na ostatnią chwilę: Regularna nauka jest o wiele bardziej skuteczna niż próba nauczenia się wszystkiego w jedną noc.

* Odpocznij przed sprawdzianem: Wyspany i wypoczęty umysł działa o wiele sprawniej.

Pamiętaj, sukces w matematyce to kombinacja wiedzy i praktyki. Zrozumienie teorii jest ważne, ale równie ważne jest rozwiązywanie zadań. Nie zniechęcaj się, jeśli napotkasz trudności. Każdy błąd to okazja do nauki. Powodzenia na sprawdzianie!