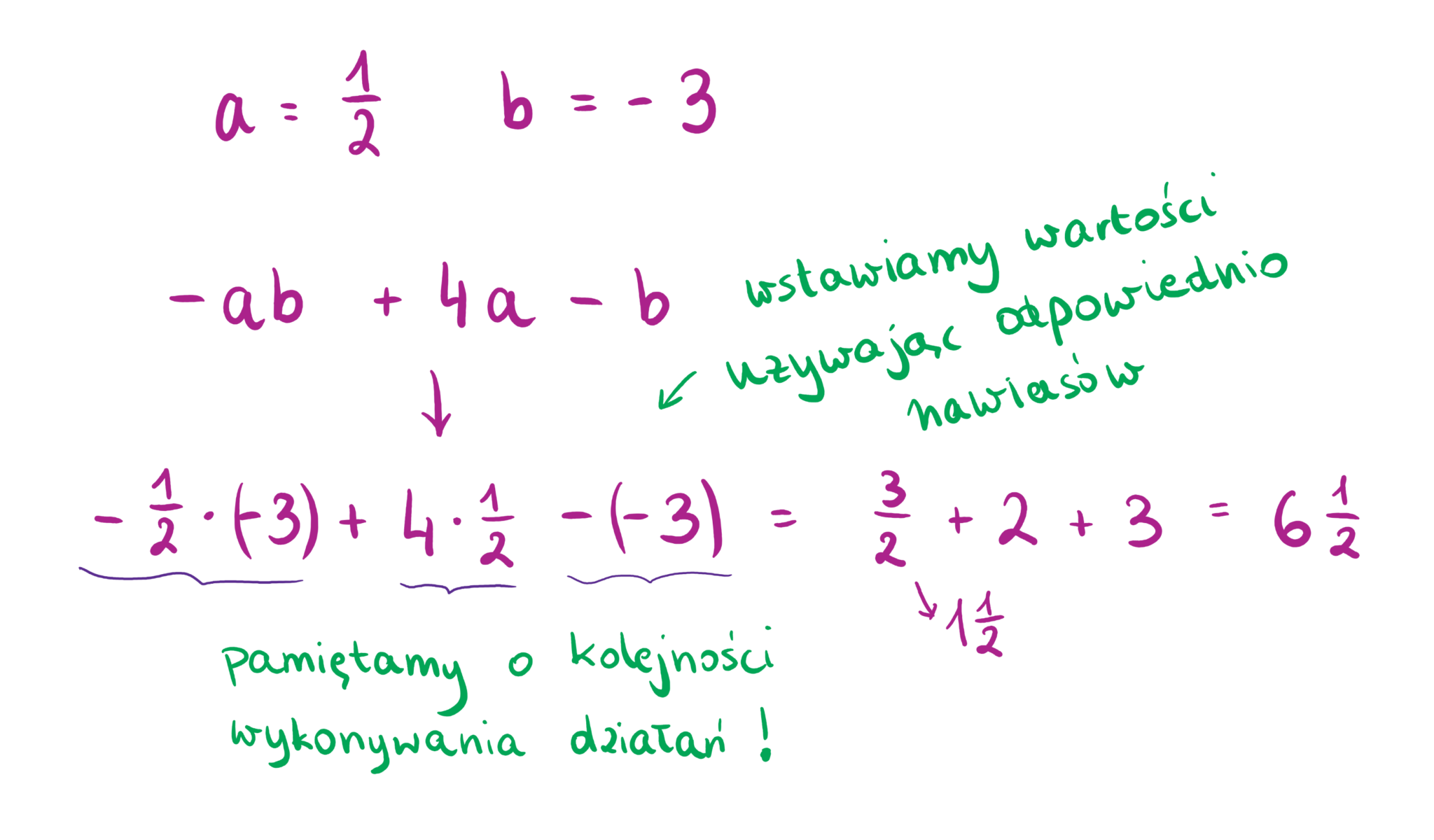Równania I Wyrażenia Algebraiczne Klasa 8

Szanowni Nauczyciele Klas Ósmych,

Temat Równania i Wyrażenia Algebraiczne jest fundamentem dalszej nauki matematyki. Zapewnienie solidnego zrozumienia tych pojęć w klasie 8. ma kluczowe znaczenie dla sukcesu uczniów w przyszłych kursach algebry i nie tylko. Ten artykuł ma na celu dostarczenie Państwu wskazówek, strategii i rozwiązań dotyczących najczęstszych problemów związanych z tym tematem.

Wyrażenia Algebraiczne: Budowanie Fundamentów

Zacznijmy od wyrażeń algebraicznych. Często uczniowie mają trudności z odróżnieniem wyrażeń od równań. Podkreśl, że wyrażenie algebraiczne to kombinacja liczb, zmiennych (reprezentowanych literami) i operacji matematycznych (dodawanie, odejmowanie, mnożenie, dzielenie), ale *nie* zawiera znaku równości.

Wprowadzenie do Zmiennych

Kluczowe jest wyjaśnienie, czym są zmienne. Używaj konkretnych przykładów. Powiedzmy, że mamy problem: "Jan ma x jabłek." Co to znaczy x? Wyjaśnij, że x reprezentuje nieznaną liczbę jabłek. To może być dowolna liczba. Pokaż uczniom, że zmienne to narzędzie do reprezentowania nieznanych wartości w problemach matematycznych.

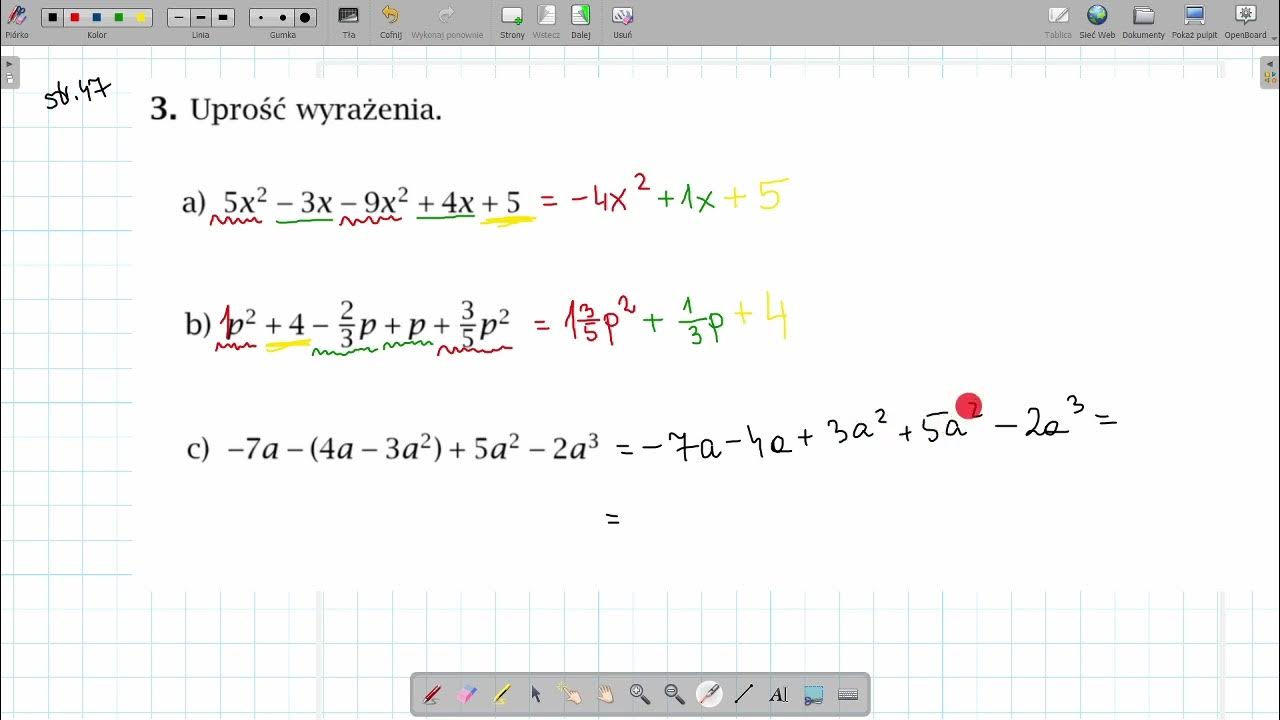
Upraszczanie Wyrażeń Algebraicznych

Naucz uczniów, jak upraszczać wyrażenia algebraiczne. Obejmuje to łączenie wyrazów podobnych. Wykorzystaj wizualne reprezentacje, np. kolorowe klocki, aby pokazać, że 3x + 2x to to samo co 5x. Unikaj wprowadzania skomplikowanych przykładów na samym początku. Zacznij od prostych kombinacji i stopniowo zwiększaj trudność.

Wskazówka: Graj w gry! Użyj kart z wyrażeniami algebraicznymi i poproś uczniów o łączenie wyrazów podobnych. To angażujący sposób na naukę.

Równania Algebraiczne: Znajdowanie Niewiadomej

Następnie przechodzimy do równań algebraicznych. Równanie algebraiczne to stwierdzenie, że dwa wyrażenia algebraiczne są równe. Zawiera ono znak równości (=). Celem rozwiązywania równania jest znalezienie wartości zmiennej (lub zmiennych), która sprawia, że równanie jest prawdziwe.

Podstawowe Zasady Rozwiązywania Równań

Wprowadź podstawowe zasady rozwiązywania równań: dodawanie, odejmowanie, mnożenie i dzielenie obu stron równania przez tę samą liczbę (z wyjątkiem dzielenia przez zero!). Wyjaśnij to za pomocą analogii wagi szalkowej. Równanie jest w równowadze, a dodawanie lub odejmowanie czegokolwiek po jednej stronie wymaga zrobienia tego samego po drugiej stronie, aby zachować równowagę.

Przykład: x + 3 = 7. Aby znaleźć x, musimy odjąć 3 od obu stron: x + 3 - 3 = 7 - 3, więc x = 4.

Typowe Błędy i Jak Ich Unikać

Istnieją typowe błędy, które uczniowie popełniają przy rozwiązywaniu równań. Często mylą kolejność operacji (PEMDAS/BODMAS). Upewnij się, że uczniowie doskonale rozumieją tę kolejność. Innym błędem jest dodawanie lub odejmowanie tylko od jednej strony równania. Podkreśl, że *wszystkie* operacje muszą być wykonywane po obu stronach.

Równania z Wieloma Krokami

Po opanowaniu podstawowych równań, wprowadź równania z wieloma krokami. Wymagają one połączenia kilku operacji w celu wyizolowania zmiennej. Naucz uczniów organizowania swojej pracy. Kroki powinny być wyraźnie zapisane, aby mogli śledzić swój proces myślowy i łatwo identyfikować błędy.

Przykład: 2x + 5 = 11. Najpierw odejmujemy 5 od obu stron: 2x = 6. Następnie dzielimy obie strony przez 2: x = 3.

Strategie Angażujące Uczniów

Zaangażowanie uczniów jest kluczowe dla zrozumienia Równań i Wyrażeń Algebraicznych. Oto kilka strategii:

Gry matematyczne: Użyj gier online lub planszowych, które koncentrują się na rozwiązywaniu równań.
Przykłady z życia wzięte: Stosuj przykłady, które są bliskie uczniom. Na przykład, obliczanie kosztu zakupu kilku przedmiotów w sklepie.
Praca w grupach: Pozwól uczniom pracować razem, aby rozwiązywać problemy. To sprzyja dyskusji i wzajemnemu uczeniu się.
Wykorzystanie technologii: Skorzystaj z kalkulatorów graficznych lub oprogramowania do algebry, aby wizualizować równania i wyrażenia.

Przykłady Zastosowań w Życiu Codziennym

Pokaż uczniom, że algebra jest użyteczna w życiu codziennym. Przykłady obejmują: planowanie budżetu, obliczanie odległości i czasu podróży, gotowanie (przeliczanie proporcji w przepisach), a nawet analizowanie danych sportowych. Im bardziej uczniowie widzą praktyczne zastosowanie algebry, tym bardziej będą zaangażowani w naukę.

Podsumowanie i Dalsze Kroki

Podsumowując, nauczanie Równań i Wyrażeń Algebraicznych w klasie 8. wymaga cierpliwości, jasnych wyjaśnień i angażujących strategii. Pamiętaj, aby zacząć od fundamentów, unikać typowych błędów i pokazywać uczniom, jak algebra jest przydatna w prawdziwym życiu. Regularne powtórki i ćwiczenia są kluczem do utrwalenia wiedzy.

Powodzenia w nauczaniu!