Równania I Nierówności Z Wartością Bezwzględną Sprawdzian

Witaj, młody matematyku! Przygotowujesz się do sprawdzianu z równań i nierówności z wartością bezwzględną? Doskonale! W tym artykule znajdziesz porcję wiedzy, która pomoże Ci się uporać z każdym zadaniem. Przejdziemy przez różne typy zadań, pokażemy metody rozwiązywania i udzielimy praktycznych wskazówek. Zapnij pasy, zaczynamy!

Zacznijmy od podstaw. Przypomnijmy sobie definicję wartości bezwzględnej. Wartość bezwzględna liczby x, oznaczana jako |x|, to jej odległość od zera na osi liczbowej. Innymi słowy:

|x| = x, gdy x ≥ 0 |x| = -x, gdy x < 0

To kluczowa definicja, od której zależy całe nasze dalsze rozumowanie. Bez niej ani rusz! Pamiętaj o niej, bo będzie nam towarzyszyć w każdym przykładzie.

Rozwiązywanie równań z wartością bezwzględną często sprowadza się do rozważenia dwóch przypadków: jeden, gdy wyrażenie pod wartością bezwzględną jest nieujemne, i drugi, gdy jest ujemne.

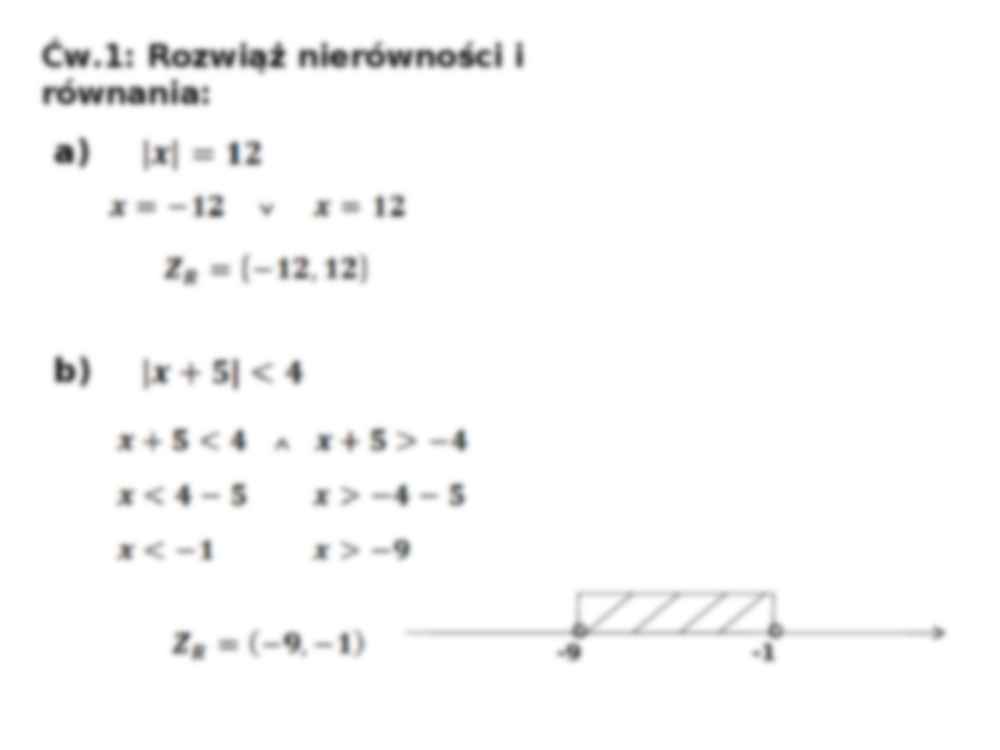
Przykład 1: Rozwiąż równanie |x - 2| = 3

Rozważamy dwa przypadki:

x - 2 ≥ 0, czyli x ≥ 2. Wtedy |x - 2| = x - 2. Mamy równanie:

x - 2 = 3 x = 5

Ponieważ 5 ≥ 2, rozwiązanie x = 5 jest poprawne.

x - 2 < 0, czyli x < 2. Wtedy |x - 2| = -(x - 2) = -x + 2. Mamy równanie:

-x + 2 = 3 -x = 1 x = -1

Ponieważ -1 < 2, rozwiązanie x = -1 jest poprawne.

Zatem rozwiązaniami równania |x - 2| = 3 są x = 5 i x = -1.

Przykład 2: Rozwiąż równanie |2x + 1| = 5

2x + 1 ≥ 0, czyli x ≥ -1/2. Wtedy |2x + 1| = 2x + 1. Mamy równanie:

2x + 1 = 5 2x = 4 x = 2

Ponieważ 2 ≥ -1/2, rozwiązanie x = 2 jest poprawne.

2x + 1 < 0, czyli x < -1/2. Wtedy |2x + 1| = -(2x + 1) = -2x - 1. Mamy równanie:

-2x - 1 = 5 -2x = 6 x = -3

Ponieważ -3 < -1/2, rozwiązanie x = -3 jest poprawne.

Zatem rozwiązaniami równania |2x + 1| = 5 są x = 2 i x = -3.

Przykład 3: Rozwiąż równanie |3x - 4| = -2

Wartość bezwzględna nigdy nie jest ujemna. Zatem to równanie nie ma rozwiązań.

Nierówności z wartością bezwzględną rozwiązuje się podobnie jak równania, z uwzględnieniem kierunku nierówności. Pamiętajmy, że nierówności to nie to samo, co równania.

Przykład 4: Rozwiąż nierówność |x - 1| < 2

Rozważamy dwa przypadki:

x - 1 ≥ 0, czyli x ≥ 1. Wtedy |x - 1| = x - 1. Mamy nierówność:

x - 1 < 2 x < 3

Zatem w tym przypadku mamy 1 ≤ x < 3.

x - 1 < 0, czyli x < 1. Wtedy |x - 1| = -(x - 1) = -x + 1. Mamy nierówność:

-x + 1 < 2 -x < 1 x > -1

Zatem w tym przypadku mamy -1 < x < 1.

Łącząc oba przypadki, otrzymujemy -1 < x < 3. Czyli rozwiązaniem nierówności jest przedział (-1, 3).

Przykład 5: Rozwiąż nierówność |2x + 3| > 1

2x + 3 ≥ 0, czyli x ≥ -3/2. Wtedy |2x + 3| = 2x + 3. Mamy nierówność:

2x + 3 > 1 2x > -2 x > -1

Zatem w tym przypadku mamy x > -1.

2x + 3 < 0, czyli x < -3/2. Wtedy |2x + 3| = -(2x + 3) = -2x - 3. Mamy nierówność:

-2x - 3 > 1 -2x > 4 x < -2

Zatem w tym przypadku mamy x < -2.

Łącząc oba przypadki, otrzymujemy x < -2 lub x > -1. Czyli rozwiązaniem nierówności jest suma przedziałów (-∞, -2) ∪ (-1, ∞).

Przykład 6: Rozwiąż nierówność |x + 5| ≤ 0

Wartość bezwzględna jest zawsze nieujemna. Zatem |x + 5| ≤ 0 tylko wtedy, gdy |x + 5| = 0.

x + 5 = 0 x = -5

Zatem rozwiązaniem nierówności jest x = -5.

Bardziej Złożone Równania i Nierówności

Czasem spotkamy równania i nierówności, które wymagają kilku kroków, zanim będziemy mogli zastosować standardową metodę. Najczęściej spotykane komplikacje to obecność wartości bezwzględnej po obu stronach równania lub nierówności, lub występowanie wartości bezwzględnej wewnątrz innej wartości bezwzględnej.

Przykład 7: Rozwiąż równanie |x - 1| = |2x + 3|

Rozważamy cztery przypadki ( wynikają one z kombinacji znaków wyrażeń w wartościach bezwzględnych):

x - 1 ≥ 0 i 2x + 3 ≥ 0. Wtedy x ≥ 1 i x ≥ -3/2. Zatem x ≥ 1. Mamy równanie:

x - 1 = 2x + 3 -x = 4 x = -4

To rozwiązanie nie spełnia warunku x ≥ 1, więc je odrzucamy.

x - 1 < 0 i 2x + 3 ≥ 0. Wtedy x < 1 i x ≥ -3/2. Zatem -3/2 ≤ x < 1. Mamy równanie:

-(x - 1) = 2x + 3 -x + 1 = 2x + 3 -3x = 2 x = -2/3

To rozwiązanie spełnia warunek -3/2 ≤ x < 1, więc jest poprawne.

x - 1 ≥ 0 i 2x + 3 < 0. Wtedy x ≥ 1 i x < -3/2. To jest niemożliwe.
x - 1 < 0 i 2x + 3 < 0. Wtedy x < 1 i x < -3/2. Zatem x < -3/2. Mamy równanie:

-(x - 1) = -(2x + 3) -x + 1 = -2x - 3 x = -4

To rozwiązanie spełnia warunek x < -3/2, więc jest poprawne.

Zatem rozwiązaniami równania |x - 1| = |2x + 3| są x = -2/3 i x = -4.

Przykład 8: Rozwiąż nierówność |x - 2| ≤ |x + 1|

Podnosimy obie strony do kwadratu (można to zrobić, bo obie strony są nieujemne):

(x - 2)^2 ≤ (x + 1)^2 x^2 - 4x + 4 ≤ x^2 + 2x + 1 -6x ≤ -3 x ≥ 1/2

Zatem rozwiązaniem nierówności jest przedział [1/2, ∞).

Wartość Bezwzględna w Wartości Bezwzględnej

Zadania tego typu bywają nieco mylące, ale pamiętaj, że najważniejsza jest systematyczność. Rozpoczynamy od wewnętrznej wartości bezwzględnej, a następnie przechodzimy do zewnętrznej.

Przykład 9: Rozwiąż równanie ||x - 1| - 2| = 1

Rozważamy dwa przypadki:

|x - 1| - 2 ≥ 0. Wtedy ||x - 1| - 2| = |x - 1| - 2. Mamy równanie:

|x - 1| - 2 = 1 |x - 1| = 3

Teraz rozwiązujemy |x - 1| = 3, tak jak w przykładzie 1. Otrzymujemy x = 4 lub x = -2. Sprawdzamy, czy |x - 1| - 2 ≥ 0 dla obu tych rozwiązań. Dla x = 4: |4 - 1| - 2 = 3 - 2 = 1 ≥ 0. Zatem x = 4 jest poprawne. Dla x = -2: |-2 - 1| - 2 = 3 - 2 = 1 ≥ 0. Zatem x = -2 jest poprawne.

|x - 1| - 2 < 0. Wtedy ||x - 1| - 2| = -(|x - 1| - 2) = -|x - 1| + 2. Mamy równanie:

-|x - 1| + 2 = 1 -|x - 1| = -1 |x - 1| = 1

Teraz rozwiązujemy |x - 1| = 1. Otrzymujemy x = 2 lub x = 0. Sprawdzamy, czy |x - 1| - 2 < 0 dla obu tych rozwiązań. Dla x = 2: |2 - 1| - 2 = 1 - 2 = -1 < 0. Zatem x = 2 jest poprawne. Dla x = 0: |0 - 1| - 2 = 1 - 2 = -1 < 0. Zatem x = 0 jest poprawne.

Zatem rozwiązaniami równania ||x - 1| - 2| = 1 są x = 4, x = -2, x = 2 i x = 0.

Wskazówki Przed Sprawdzianem

Powtórz definicję wartości bezwzględnej. Upewnij się, że doskonale rozumiesz, co oznacza |x|.
Przejrzyj rozwiązane przykłady. Spróbuj rozwiązać je ponownie samodzielnie.
Rozwiąż dodatkowe zadania. Im więcej ćwiczysz, tym lepiej opanujesz materiał.
Zwracaj uwagę na znaki. Błędy w znakach to częsty problem przy rozwiązywaniu równań i nierówności.
Sprawdzaj rozwiązania. Po znalezieniu rozwiązania zawsze sprawdź, czy spełnia ono warunki początkowe.

Pamiętaj, że kluczem do sukcesu jest praktyka. Im więcej zadań rozwiążesz, tym pewniej poczujesz się na sprawdzianie. Powodzenia!